Reinforced diffusions as models of memory-mediated animal movement
- PMID: 36987616
- PMCID: PMC10050924
- DOI: 10.1098/rsif.2022.0700
Reinforced diffusions as models of memory-mediated animal movement
Abstract
How memory shapes animals' movement paths is a topic of growing interest in ecology, with connections to planning for conservation and climate change. Empirical studies suggest that memory has both temporal and spatial components, and can include both attractive and aversive elements. Here, we introduce reinforced diffusions (the continuous time counterpart of reinforced random walks) as a modelling framework for understanding the role that memory plays in determining animal movements. This framework includes reinforcement via functions of time before present and of distance away from a current location. Focusing on the interplay between memory and central place attraction (a component of home ranging behaviour), we explore patterns of space usage that result from the reinforced diffusion. Our efforts identify three qualitatively different behaviours: bounded wandering behaviour that does not collapse spatially, collapse to a very small area, and, most intriguingly, convergence to a cycle. Subsequent applications show how reinforced diffusion can create movement trajectories emulating the learning of movement routes by homing pigeons and consolidation of ant travel paths. The mathematically explicit manner with which assumptions about the structure of memory can be stated and subsequently explored provides linkages to biological concepts like an animal's 'immediate surroundings' and memory decay.
Keywords: movement ecology; reinforced diffusion; reinforced random walk; spatial memory; time since last visit.
Conflict of interest statement
We declare we have no competing interests.
Figures
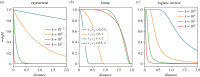
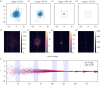
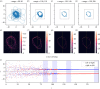
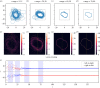
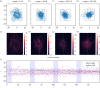
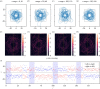
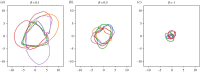
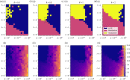
Similar articles
-
Spatial movement with distributed memory.J Math Biol. 2021 Mar 11;82(4):33. doi: 10.1007/s00285-021-01588-0. J Math Biol. 2021. PMID: 33709247
-
Random walk models in biology.J R Soc Interface. 2008 Aug 6;5(25):813-34. doi: 10.1098/rsif.2008.0014. J R Soc Interface. 2008. PMID: 18426776 Free PMC article. Review.
-
Three-dimensional random walk models of individual animal movement and their application to trap counts modelling.J Theor Biol. 2021 Sep 7;524:110728. doi: 10.1016/j.jtbi.2021.110728. Epub 2021 Apr 23. J Theor Biol. 2021. PMID: 33895179
-
Linking movement behaviour, dispersal and population processes: is individual variation a key?J Anim Ecol. 2009 Sep;78(5):894-906. doi: 10.1111/j.1365-2656.2009.01534.x. Epub 2009 Mar 6. J Anim Ecol. 2009. PMID: 19302396 Review.
-
What's your move? Movement as a link between personality and spatial dynamics in animal populations.Ecol Lett. 2017 Jan;20(1):3-18. doi: 10.1111/ele.12708. Ecol Lett. 2017. PMID: 28000433
Cited by
-
Lévy movements and a slowly decaying memory allow efficient collective learning in groups of interacting foragers.PLoS Comput Biol. 2023 Oct 16;19(10):e1011528. doi: 10.1371/journal.pcbi.1011528. eCollection 2023 Oct. PLoS Comput Biol. 2023. PMID: 37844076 Free PMC article.
-
Identifying signals of memory from observations of animal movements.Mov Ecol. 2024 Nov 18;12(1):72. doi: 10.1186/s40462-024-00510-9. Mov Ecol. 2024. PMID: 39558435 Free PMC article. Review.
References
-
- Mueller T, Fagan WF. 2008. Search and navigation in dynamic environments—from individual behaviors to population distributions. Oikos 117, 654-664. (10.1111/j.0030-1299.2008.16291.x) - DOI
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources

