On predictive inference for intractable models via approximate Bayesian computation

doi:10.1007/s11222-022-10163-6

. 2023;33(2):42.

doi: 10.1007/s11222-022-10163-6. Epub 2023 Feb 9.

On predictive inference for intractable models via approximate Bayesian computation

Marko Järvenpää¹, Jukka Corander^{1

2

3}

Affiliations

¹ Department of Biostatistics, University of Oslo, Oslo, Norway.
² Department of Mathematics and Statistics, Helsinki Institute of Information Technology (HIIT), University of Helsinki, Helsinki, Finland.
³ Wellcome Sanger Institute, Hinxton, Cambridgeshire, UK.

PMID: 36785730
PMCID: PMC9911513
DOI: 10.1007/s11222-022-10163-6

On predictive inference for intractable models via approximate Bayesian computation

Marko Järvenpää et al. Stat Comput. 2023.

. 2023;33(2):42.

doi: 10.1007/s11222-022-10163-6. Epub 2023 Feb 9.

Authors

Marko Järvenpää¹, Jukka Corander^{1

2

3}

Affiliations

¹ Department of Biostatistics, University of Oslo, Oslo, Norway.
² Department of Mathematics and Statistics, Helsinki Institute of Information Technology (HIIT), University of Helsinki, Helsinki, Finland.
³ Wellcome Sanger Institute, Hinxton, Cambridgeshire, UK.

PMID: 36785730
PMCID: PMC9911513
DOI: 10.1007/s11222-022-10163-6

Abstract

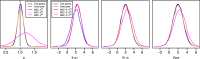
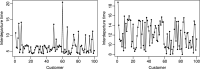
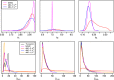
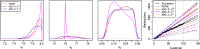
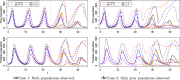
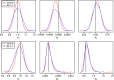
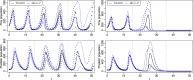
Approximate Bayesian computation (ABC) is commonly used for parameter estimation and model comparison for intractable simulator-based statistical models whose likelihood function cannot be evaluated. In this paper we instead investigate the feasibility of ABC as a generic approximate method for predictive inference, in particular, for computing the posterior predictive distribution of future observations or missing data of interest. We consider three complementary ABC approaches for this goal, each based on different assumptions regarding which predictive density of the intractable model can be sampled from. The case where only simulation from the joint density of the observed and future data given the model parameters can be used for inference is given particular attention and it is shown that the ideal summary statistic in this setting is minimal predictive sufficient instead of merely minimal sufficient (in the ordinary sense). An ABC prediction approach that takes advantage of a certain latent variable representation is also investigated. We additionally show how common ABC sampling algorithms can be used in the predictive settings considered. Our main results are first illustrated by using simple time-series models that facilitate analytical treatment, and later by using two common intractable dynamic models.

Supplementary information: The online version contains supplementary material available at 10.1007/s11222-022-10163-6.

Keywords: Approximate Bayesian computation; Intractable dynamic models; Posterior predictive distribution; Predictive sufficiency; Selection of summary statistics.

PubMed Disclaimer

Figures

**Fig. 1**
Illustration of the effect of summary statistics $s^{(1)} (y) = {\bar{y}}_{ϕ}$ , $s^{(2)} (y) = ({\bar{y}}_{ϕ}, y_{n})$ and $s^{(3)} (y) = {\overset{˚}{y}}_{ϕ} = {\bar{y}}_{ϕ} + ϕ y_{n}$ on the ABC approximation accuracy in Example 3.1. *The first plot* on the left shows the ABC(-P/F) posterior for c and *the three other plots* the ABC-P posterior predictive distribution at some future time points. The black vertical line shows the true value of c used to generate the data and the red lines show the exact Gaussian posteriors obtained using (16) and (B.31) of Supplementary material with $h = 0$

**Fig. 2**
Observed interdeparture times $y = (y_{1}, \dots, y_{n})$ with $n = 100$ used in the M/G/1 experiments. *Left plot:* The case of Sect. 5.1.2 where the queue length is varying. Occasional large interdeparture times suggest that the queue could be then empty. *Right plot:* The case of Sect. 5.1.3 where the queue length tends to be growing

**Fig. 3**
Results for the M/G/1 experiments of Sect. 5.1.2. *Top row:* Marginal posterior distributions computed using MCMC and ABC for parameters $θ$ . *Bottom row:* Predictive distribution based on the true parameter $θ_{true}$ (“True param.”) and posterior predictive distributions computed using MCMC and ABC approaches for the waiting times of some future customers. The right tail of the ABC-P posterior predictive based on $s^{(0)}$ is truncated to ease visualization

**Fig. 4**
Typical results for the M/G/1 experiment of Sect. 5.1.3. *The first three plots* on the left show the marginal posteriors for $θ$ . *The fourth plot* illustrates the predictive densities for $ω$ (solid lines: the median, dot-dashed lines: 75% credible interval (CI), dashed lines: 90% CI). Note that these lines are also drawn for the observed customers in the case of ABC-P. The vertical gray line shows the first future customer. The black rings show the unobserved waiting times not used for inference

**Fig. 5**
Typical results for the Lotka–Volterra experiments of Sect. 5.2.2. The vertical gray line shows where the prediction interval starts and the black circles show the observations. The solid lines show the median and the dashed lines the $90 %$ CI. These lines are also drawn in $[0, τ_{1}]$ to demonstrate that the observed data is not conditioned on exactly in ABC. “True param.” shows the ideal predictive distribution based on $θ_{true}$ (case 1) and its approximation (case 2). The prey population size is truncated in case 2 because the predator population can die out with a non-negligible posterior probability in which case the prey population starts to grow exponentially fast

**Fig. 6**
Posterior distributions for the parameters of the Lotka–Volterra experiments corresponding to Fig. 5 and Sect. 5.2.2. *Top row:* Case 1 where both populations are observed. *Bottom row:* Case 2 where only prey population is observed. The black vertical line shows the true value of the parameter

**Fig. 7**
Results for the Lotka–Volterra experiment of Sect. 5.2.3 with two sets of observed data. The vertical gray lines indicate the unobserved time interval [15, 36] and the black circles show the observations. The solid lines show the median and the dashed lines the $90 %$ CI. “True param.” shows the ideal predictive distribution based on $θ_{true}$ (right column) and its approximation (left column)

See this image and copyright information in PMC

References

1. Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B. 2010;72(3):269–342.
1. Barber S, Voss J, Webster M. The rate of convergence for approximate Bayesian computation. Electron. J. Stat. 2015;9(1):80–105.
1. Beaumont MA, Cornuet J-M, Marin J-M, Robert CP. Adaptive approximate Bayesian computation. Biometrika. 2009;96(4):983–990.
1. Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162(4):2025–2035. - PMC - PubMed
1. Bernardo JM, Smith AFM. Bayesian Theory. Hoboken: Wiley; 1994.

LinkOut - more resources

Full Text Sources
- Europe PubMed Central
- PubMed Central

[1] Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B. 2010;72(3):269–342.

[2] Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B. 2010;72(3):269–342.

[3] Barber S, Voss J, Webster M. The rate of convergence for approximate Bayesian computation. Electron. J. Stat. 2015;9(1):80–105.

[4] Barber S, Voss J, Webster M. The rate of convergence for approximate Bayesian computation. Electron. J. Stat. 2015;9(1):80–105.

[5] Beaumont MA, Cornuet J-M, Marin J-M, Robert CP. Adaptive approximate Bayesian computation. Biometrika. 2009;96(4):983–990.

[6] Beaumont MA, Cornuet J-M, Marin J-M, Robert CP. Adaptive approximate Bayesian computation. Biometrika. 2009;96(4):983–990.

[7] Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162(4):2025–2035. - PMC - PubMed

[8] Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162(4):2025–2035. - PMC - PubMed

[9] Bernardo JM, Smith AFM. Bayesian Theory. Hoboken: Wiley; 1994.

[10] Bernardo JM, Smith AFM. Bayesian Theory. Hoboken: Wiley; 1994.

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

On predictive inference for intractable models via approximate Bayesian computation

Affiliations

On predictive inference for intractable models via approximate Bayesian computation

Authors

Affiliations

Abstract

Figures

Similar articles

References

LinkOut - more resources

Full Text Sources