Setting Boundaries for Statistical Mechanics
- PMID: 36432117
- PMCID: PMC9696510
- DOI: 10.3390/molecules27228017
Setting Boundaries for Statistical Mechanics
Abstract
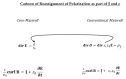
Statistical mechanics has grown without bounds in space. Statistical mechanics of noninteracting point particles in an unbounded perfect gas is widely used to describe liquids like concentrated salt solutions of life and electrochemical technology, including batteries. Liquids are filled with interacting molecules. A perfect gas is a poor model of a liquid. Statistical mechanics without spatial bounds is impossible as well as imperfect, if molecules interact as charged particles, as nearly all atoms do. The behavior of charged particles is not defined until boundary structures and values are defined because charges are governed by Maxwell's partial differential equations. Partial differential equations require boundary structures and conditions. Boundary conditions cannot be defined uniquely 'at infinity' because the limiting process that defines 'infinity' includes such a wide variety of structures and behaviors, from elongated ellipses to circles, from light waves that never decay, to dipolar fields that decay steeply, to Coulomb fields that hardly decay at all. Boundaries and boundary conditions needed to describe matter are not prominent in classical statistical mechanics. Statistical mechanics of bounded systems is described in the EnVarA system of variational mechanics developed by Chun Liu, more than anyone else. EnVarA treatment does not yet include Maxwell equations.
Keywords: EnVarA; Maxwell equations; boundary conditions; statistical mechanics; variational methods.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


Similar articles
-
Energy variational analysis of ions in water and channels: Field theory for primitive models of complex ionic fluids.J Chem Phys. 2010 Sep 14;133(10):104104. doi: 10.1063/1.3476262. J Chem Phys. 2010. PMID: 20849161 Free PMC article.
-
Multiple Scales in the Simulation of Ion Channels and Proteins.J Phys Chem C Nanomater Interfaces. 2010 Oct 21;114(48):20719-20733. doi: 10.1021/jp106760t. J Phys Chem C Nanomater Interfaces. 2010. PMID: 21135913 Free PMC article.
-
Maxwell's Demon in Quantum Mechanics.Entropy (Basel). 2020 Feb 27;22(3):269. doi: 10.3390/e22030269. Entropy (Basel). 2020. PMID: 33286043 Free PMC article.
-
Maxwell electromagnetism as an emergent phenomenon in condensed matter.Philos Trans A Math Phys Eng Sci. 2016 Aug 28;374(2075):20160093. doi: 10.1098/rsta.2016.0093. Philos Trans A Math Phys Eng Sci. 2016. PMID: 27458263 Review.
-
Why Noether's theorem applies to statistical mechanics.J Phys Condens Matter. 2022 Apr 21;34(21). doi: 10.1088/1361-648X/ac5b47. J Phys Condens Matter. 2022. PMID: 35255482 Review.
Cited by
-
H-Bonds in Crambin: Coherence in an α-Helix.ACS Omega. 2023 Apr 3;8(15):13920-13934. doi: 10.1021/acsomega.3c00181. eCollection 2023 Apr 18. ACS Omega. 2023. PMID: 37091420 Free PMC article.
References
-
- Feynman R.P. Forces in molecules. Phys. Rev. 1939;56:340–343. doi: 10.1103/PhysRev.56.340. - DOI
-
- Feynman R.P., Leighton R.B., Sands M. The Feynman: Lectures on Physics, Volume 1, 2, 3. Addison-Wesley Publishing Co.; New York, NY, USA: 1963. [(accessed on 2 October 2022)]. Available online: http://www.feynmanlectures.caltech.edu/II_toc.html.
-
- Oriols X., Ferry D.K. Why engineers are right to avoid the quantum reality offered by the orthodox theory?[point of view] Proc. IEEE. 2021;109:955–961. doi: 10.1109/JPROC.2021.3067110. - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

