Guiding principle of reservoir computing based on "small-world" network

doi:10.1038/s41598-022-21235-y

. 2022 Oct 6;12(1):16697.

doi: 10.1038/s41598-022-21235-y.

Guiding principle of reservoir computing based on "small-world" network

Ken-Ichi Kitayama^{1

2}

Affiliations

¹ National Institute of Information and Communications Technology, Tokyo, 184-8795, Japan. kitayama@ieee.org.
² Hamamatsu Photonics K.K., Hamamatsu, 434-8601, Japan. kitayama@ieee.org.

PMID: 36202989
PMCID: PMC9537422
DOI: 10.1038/s41598-022-21235-y

Guiding principle of reservoir computing based on "small-world" network

Ken-Ichi Kitayama. Sci Rep. 2022.

. 2022 Oct 6;12(1):16697.

doi: 10.1038/s41598-022-21235-y.

Author

Ken-Ichi Kitayama^{1

2}

Affiliations

¹ National Institute of Information and Communications Technology, Tokyo, 184-8795, Japan. kitayama@ieee.org.
² Hamamatsu Photonics K.K., Hamamatsu, 434-8601, Japan. kitayama@ieee.org.

PMID: 36202989
PMCID: PMC9537422
DOI: 10.1038/s41598-022-21235-y

Abstract

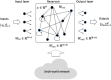
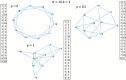
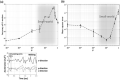
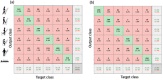
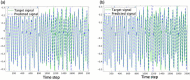
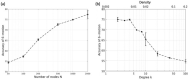
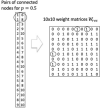
Reservoir computing is a computational framework of recurrent neural networks and is gaining attentions because of its drastically simplified training process. For a given task to solve, however, the methodology has not yet been established how to construct an optimal reservoir. While, "small-world" network has been known to represent networks in real-world such as biological systems and social community. This network is categorized amongst those that are completely regular and totally disordered, and it is characterized by highly-clustered nodes with a short path length. This study aims at providing a guiding principle of systematic synthesis of desired reservoirs by taking advantage of controllable parameters of the small-world network. We will validate the methodology using two different types of benchmark tests-classification task and prediction task.

PubMed Disclaimer

Conflict of interest statement

The author declares no competing interests.

Figures

**Figure 1**
Reservoir computing architecture. Input weight matrix W_in is a fixed N × L matrix where N is the number of nodes in the reservoir, and L is the dimension of the inputs at each time step. Reservoir weight matrix Wres is a fixed N × N matrix, which is typically sparse with nonzero elements having an either a symmetrical uniform, discrete bi-valued, or normal distribution centered around zero. Output weight matrix Wout is a learned $M \times N$ matrix where $M$ is the number of classes of the output data.

**Figure 2**
Architectures of 10-node ( $N = 10$ ) networks with the node degree $k = 2$ ; regularly connected ( $p = 0$ ) on the l.h.s. on the top, modestly disordered ( $p = 0.5$ ) on the r.h.s. on the top, and totally disordered ( $p = 1$ ) at the bottom. Each node is connected with four (= 2 $k)$ neighboring nodes. Each table represents the pairs of nodes for each $p$ . For example, node#1 is connected with nodes#2, 3, 9, and 10 for the case with $p = 0$ .

**Figure 3**
a Clustering coefficient $C (p) / C (0)$ and average path length or hop count $L (p) / L (0)$ vs. probability of rewiring p for the case with 1000-node ( $N = 1000$ ) and the node degrees $k = 4$ and 6. Range roughly $p =$ 0.01–0.7 of small-world is indicated by the shaded area. b Clustering coefficients $C (p) / C (0)$ and average path lengths $L (p) / L (0)$ vs. probability of rewiring p for the case with the node degrees $k = 20$ and 100.

**Figure 4**
(a) Classification accuracy of human 6-activity vs. probability of rewiring $p$ for the case with $N = 1000$ and $k = 4$ . The accuracy is maximized to be 74.9% at $p = 0.5$ . For an example, the temporal waveforms of accelerations of walking on x-, y, and z-axes are also shown on the bottom. (b) Prediction accuracy represented by the mean square error (MSE) of MG chaotic signal vs. $p$ for the case with $N = 1000$ and $k = 4$ . MSE is minimized to be $4.98 \times 10^{- 6}$ at $p = 0.1$ .

**Figure 5**
Confusion matrices of human 6-activity classification are compared for 1000-node reservoir. (a) Reservoir weight matrix $W_{res}$ of small-world network $(k, p) = (4, 0.5)$ . Accuracy (in green) is 75.2%. (b) Conventional sparsely random matrix $W_{res}$ with the density of 0.008. Accuracy is 73.0%.

**Figure 6**
2000 timestep-long waveforms of predicted and that of target MG chaotic time series for 1000-node reservoir. (a) Result of reservoir weight matrix $W_{res}$ of 1000-node small-world network $(k, p) = (4, 0.1)$ . Mean square error (MSE) is $2.46 \times 10^{- 6}$ . (b) Conventional sparsely random matrix $W_{res}$ with the density of 0.008. MSE is $1.38 \times 10^{- 6}$ . Results of the two benchmark tests are summarized in Table 1.

**Figure 7**
Performance of human activity classification using reservoir weight matrix $W_{res}$ generated from the Watts–Strogatz graph. (a) Classification accuracy versus the number of nodes $N$ . Node degree $k = 4$ and the probability of rewiring $p = 0.5$ within the range of small-world network are assumed. (b) Classification accuracy against the degree of node $k$ . $p = 0.5$ of 1000-node small-world network is assumed. Horizontal axis on the top is density of matrix $W_{res}$ calculated by Eq. (6).

**Figure 8**
Method for generating the weight matrix $W_{res}$ of the reservoir of 10-node ( $N = 10$ ) networks with $(k, p) = (2, 0.5)$ . Table of pairs of connected nodes on the l.h.s. and $10 \times 10$ weight matrix $W_{res}$ . For instance, connections of node 1, pairs of nodes, $(1, 6)$ and $(1, 8)$ reflect on the weight matrix $W_{res}$ , as marked by circles.

See this image and copyright information in PMC

References

1. Verstraeten D, Schrauwen B, Stroobandt D, Van Campenhout J. Isolated word recognition with the liquid state machine: A case study. Inf. Process. Lett. 2005;95:521–528. doi: 10.1016/j.ipl.2005.05.019. - DOI
1. Lukoševicius M, Jaeger H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009;3:127–149. doi: 10.1016/j.cosrev.2009.03.005. - DOI
1. Jaeger. H. The ‘echo state’ approach to analyzing and training recurrent neural networks. Technical Report GMD Report148, German National Research Center for Information Technology (2001).
1. Jaeger H, Hass H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science. 2004;304:78–80. doi: 10.1126/science.1091277. - DOI - PubMed
1. Maass W, Natschläger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. - DOI - PubMed

MeSH terms

Actions

LinkOut - more resources

Full Text Sources

[1] Verstraeten D, Schrauwen B, Stroobandt D, Van Campenhout J. Isolated word recognition with the liquid state machine: A case study. Inf. Process. Lett. 2005;95:521–528. doi: 10.1016/j.ipl.2005.05.019. - DOI

[2] Verstraeten D, Schrauwen B, Stroobandt D, Van Campenhout J. Isolated word recognition with the liquid state machine: A case study. Inf. Process. Lett. 2005;95:521–528. doi: 10.1016/j.ipl.2005.05.019. - DOI

[3] Lukoševicius M, Jaeger H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009;3:127–149. doi: 10.1016/j.cosrev.2009.03.005. - DOI

[4] Lukoševicius M, Jaeger H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009;3:127–149. doi: 10.1016/j.cosrev.2009.03.005. - DOI

[5] Jaeger. H. The ‘echo state’ approach to analyzing and training recurrent neural networks. Technical Report GMD Report148, German National Research Center for Information Technology (2001).

[6] Jaeger. H. The ‘echo state’ approach to analyzing and training recurrent neural networks. Technical Report GMD Report148, German National Research Center for Information Technology (2001).

[7] Jaeger H, Hass H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science. 2004;304:78–80. doi: 10.1126/science.1091277. - DOI - PubMed

[8] Jaeger H, Hass H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science. 2004;304:78–80. doi: 10.1126/science.1091277. - DOI - PubMed

[9] Maass W, Natschläger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. - DOI - PubMed

[10] Maass W, Natschläger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. - DOI - PubMed

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Guiding principle of reservoir computing based on "small-world" network

Affiliations

Guiding principle of reservoir computing based on "small-world" network

Author

Affiliations

Abstract

Conflict of interest statement

Figures

Similar articles

References

MeSH terms

LinkOut - more resources

Full Text Sources