Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Oct 3;13(1):5809.
doi: 10.1038/s41467-022-33344-3.

Quantifying ethnic segregation in cities through random walks

Sandro Sousa  1   2 , Vincenzo Nicosia  3
Affiliations

Quantifying ethnic segregation in cities through random walks

Sandro Sousa et al. Nat Commun. .

Abstract

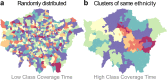
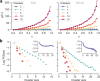
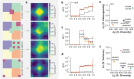
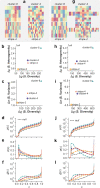
Socioeconomic segregation has an important role in the emergence of large-scale inequalities in urban areas. Most of the available measures of spatial segregation depend on the scale and size of the system under study, or neglect large-scale spatial correlations, or rely on ad-hoc parameters, making it hard to compare different systems on equal grounds. We propose here a family of non-parametric measures for spatial distributions, based on the statistics of the trajectories of random walks on graphs associated to a spatial system. These quantities provide a consistent estimation of segregation in synthetic spatial patterns, and we use them to analyse the ethnic segregation of metropolitan areas in the US and the UK. We show that the spatial diversity of ethnic distributions, as measured through diffusion on graphs, allow us to compare the ethnic segregation of urban areas having different size, shape, or peculiar microscopic characteristics, and exhibits a strong association with socio-economic deprivation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Fig. 1
Fig. 1. Fictitious maps of the association of seven ethnicities to the wards of Greater London.
a The ethnicities are distributed uniformly at random across the city, to simulate a "maximally'' homogeneous and unsegregated pattern. In this case, a random walker starting from any ward will get in touch with all the available ethnicities within a relatively small number of steps. b The same map with a substantial clustering of ethnicities imposed artificially. In this case, a walker starting in the middle of a cluster will need a lot more time to visit all the other ethnicities. This observation leads to the idea of using the statistics of Class Coverage Time to quantify the level of segregation and heterogeneity of an urban area with respect to a given variable of interest.
Fig. 2
Fig. 2. Effect of graph size and number of classes on class coverage times in synthetic spatial networks with Γ classes and random node-class association.
a Mean class coverage time μ(c) as a function of the fraction of visited classes c on a torus with 64 (left) and 256 (right) cells. Coverage times over 32 classes are significantly larger than those over 2 classes. b Size distribution of uniform clusters formed by adjacent nodes of the same class. Larger graphs allow for bigger clusters to emerge, for any number of classes Γ. The legend in a marks the corresponding distributions in b. The distributions of cluster sizes for Γ = 2 are reported in the insets.
Fig. 3
Fig. 3. Dependence of class coverage times on size, type and location of homogeneous clusters in a 2-dimensional lattice with synthetic node-class associations.
a The nodes are divided in 4 homogeneous clusters of 60 cells each, placed in the four quadrants, while the remaining 16 nodes in the fifth class are arranged, from top to bottom, as: a central cluster (cluster-center), a cluster in a corner (cluster-corner), spread in one of the quadrants (spread-quadrant), and as four small 4 × 4 clusters on each of the corners of the lattice (spread-corners). The heat-maps reporting the normalised coverage time Ci(c)/Ci(c)null for c = 0.7 clearly show the dependency on the starting node. We also report the corresponding profiles of μ(c) (b), σ(c) (c) and ϱ(c) (d), and their values in the corresponding null-model (black dashed lines). The distinct spatial constraints are consistently discriminated by the measure of spatial diversity Δϱ whilst the planes with Δμ e and Δσ (f) provide a fuller classification of the patterns.
Fig. 4
Fig. 4. Dependence of class coverage times on domain shape and size and shape of homogeneous clusters.
a The nodes are divided in 32 classes and associated uniformly at random (from top to bottom) to uniform clusters of 8 or 4 cells and to stripes of 4 or 2 cells, on a 16 × 16 lattice. g Same patterns as in a, but on a lattice with a lateral appendix. We also report the corresponding profiles of μ(c) d, j, σ(c) e, k and ϱ(c) f, l and their values in the associated null-model (black dashed lines). The distinct spatial constraints are consistently discriminated in the Δμ/Δϱ plane b, h while ΔσΔϱ c, i provides additional information about neighbouring effect.
Fig. 5
Fig. 5. Class coverage times and ethnic segregation in urban systems.
a Metropolitan areas in the US and the UK in the Δμ/Δϱ and Δσ/Δϱ planes where they are compared by the average deviation from their corresponding null-models. b Examples of the class coverage time distributions for London where the spatial diversity ϱ(c), spatial variance σ(c), spatial heterogeneity μ(c) and their values in the corresponding null-model (black dashed lines) are plotted as a function of the fraction of visited classes c. c Maps of the metropolitan areas marked in bold in a. The normalised class coverage time Ci(c)/Ci(c)null for c = 0.7 provides detailed insights about the structure of segregation at neighbourhood level.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Gelfand, A. E., Diggle, P., Guttorp, P. & Fuentes, M.Handbook of spatial statistics (CRC Press, 2010).
    1. Barthelemy, M.The Structure and Dynamics of Cities: Urban Data Analysis and Theoretical Modeling (Cambridge University Press, Cambridge, 2016).
    1. Batty, M.The New Science of Cities (MIT Press, Cambridge, Massachusetts, 2013).
    1. Pickett STA, Cadenasso ML. Landscape ecology: spatial heterogeneity in ecological systems. Science. 1995;269:331–334. doi: 10.1126/science.269.5222.331. - DOI - PubMed
    1. Irwin EG, Bockstael NE. The evolution of urban sprawl: evidence of spatial heterogeneity and increasing land fragmentation. Proc. Natl Acad. Sci. USA. 2007;104:20672–20677. doi: 10.1073/pnas.0705527105. - DOI - PMC - PubMed

Publication types