Numerical treatments for the optimal control of two types variable-order COVID-19 model

doi:10.1016/j.rinp.2022.105964

. 2022 Nov:42:105964.

doi: 10.1016/j.rinp.2022.105964. Epub 2022 Sep 5.

Numerical treatments for the optimal control of two types variable-order COVID-19 model

Nasser Sweilam¹, Seham Al-Mekhlafi^{2

3}, Salma Shatta⁴, Dumitru Baleanu^{5

6}

Affiliations

¹ Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt.
² Department of Mathematics, Faculty of Education, Sana'a University, Yemen.
³ Department of Engineering Mathematics and Physics, Future University in Egypt, Egypt.
⁴ Department of Mathematics, Faculty of Science, Helwan University, Cairo, Egypt.
⁵ Cankaya University, Department of Mathematics, Turkey.
⁶ Institute of Space Sciences, Magurele-Bucharest, Romania.

PMID: 36092971
PMCID: PMC9444160
DOI: 10.1016/j.rinp.2022.105964

Numerical treatments for the optimal control of two types variable-order COVID-19 model

Nasser Sweilam et al. Results Phys. 2022 Nov.

. 2022 Nov:42:105964.

doi: 10.1016/j.rinp.2022.105964. Epub 2022 Sep 5.

Authors

Nasser Sweilam¹, Seham Al-Mekhlafi^{2

3}, Salma Shatta⁴, Dumitru Baleanu^{5

6}

Affiliations

¹ Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt.
² Department of Mathematics, Faculty of Education, Sana'a University, Yemen.
³ Department of Engineering Mathematics and Physics, Future University in Egypt, Egypt.
⁴ Department of Mathematics, Faculty of Science, Helwan University, Cairo, Egypt.
⁵ Cankaya University, Department of Mathematics, Turkey.
⁶ Institute of Space Sciences, Magurele-Bucharest, Romania.

PMID: 36092971
PMCID: PMC9444160
DOI: 10.1016/j.rinp.2022.105964

Abstract

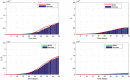
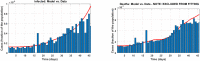
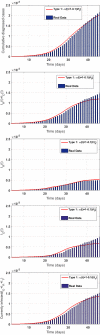
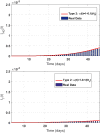
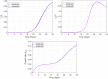
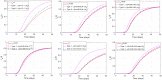
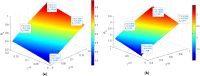
In this paper, a novel variable-order COVID-19 model with modified parameters is presented. The variable-order fractional derivatives are defined in the Caputo sense. Two types of variable order Caputo definitions are presented here. The basic reproduction number of the model is derived. Properties of the proposed model are studied analytically and numerically. The suggested optimal control model is studied using two numerical methods. These methods are non-standard generalized fourth-order Runge-Kutta method and the non-standard generalized fifth-order Runge-Kutta technique. Furthermore, the stability of the proposed methods are studied. To demonstrate the methodologies' simplicity and effectiveness, numerical test examples and comparisons with real data for Egypt and Italy are shown.

Keywords: 26A33; 49M25; 65L03; COVID-19 epidemic models; Caputo’s derivatives; Non-standard generalized Runge–Kutta methods; Optimal control theory; Stability analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

**Fig. 1**
Real data compared to the approximate solutions using GRK5M, when $α (t) = 1$ .

**Fig. 2**
Approximate solutions behavior compared to real data in Egypt, when $α (t) = 1$ .

**Fig. 3**
Behavior of the approximate solutions compared to real data, when $α (t) = 1 - 0.1 (t / t_{f})$ type one using GRK5M.

**Fig. 4**
Behavior of the approximate solutions compared to real data, when $α (t) = 1 - 0.1 (t / t_{f})$ type two using GRK5M.

**Fig. 5**
Behavior of the approximate solutions of $I_{R}$ , $I_{T}$ and the growth rate of $I_{H}$ at different methods when $α (t) = 1 - 0.004 (t / t_{f})$ .

**Fig. 6**
Optimization of the approximation solutions of $I_{H}$ at different types of $α (t)$ .

**Fig. 7**
The impact of $β^{α} (t)$ and $γ^{α} (t)$ on behavior of $R_{e}$ at $α (t) = 0.9 - 0.2 (t / t_{f})$ . Case(a) when $R_{e} < 1$ and case (b) when $R_{e} > 1$ .

**Fig. 8**
The impact of $β^{α} (t)$ and $γ^{α} (t)$ on behavior of $R_{e}$ at different value of $α (t)$ .

See this image and copyright information in PMC

References

1. World Health Organization . World HealthOrganization; 2020. Coronavirus. cited January 19, 2020. Available: https://www.who.int/health-topics/coronavirus.
1. Giordano G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med 10.1038/s41591-020-0883-7. - DOI - PMC - PubMed
1. Kumar S., Kumar R., Osman M.S., Samet B. A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer Methods Partial Differential Equations. 2021;37:1250–1268. doi: 10.1002/num.2257. - DOI
1. Mohammadi H., Kumar S., Rezapour S., Etemad S. A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals. 2021;144
1. Solís-Pérez J.E., Gómez-Aguilar J.F. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals. 2018;14:175–185.

LinkOut - more resources

Full Text Sources

[1] World Health Organization . World HealthOrganization; 2020. Coronavirus. cited January 19, 2020. Available: https://www.who.int/health-topics/coronavirus.

[2] World Health Organization . World HealthOrganization; 2020. Coronavirus. cited January 19, 2020. Available: https://www.who.int/health-topics/coronavirus.

[3] Giordano G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med 10.1038/s41591-020-0883-7. - DOI - PMC - PubMed

[4] Giordano G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med 10.1038/s41591-020-0883-7. - DOI - PMC - PubMed

[5] Kumar S., Kumar R., Osman M.S., Samet B. A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer Methods Partial Differential Equations. 2021;37:1250–1268. doi: 10.1002/num.2257. - DOI

[6] Kumar S., Kumar R., Osman M.S., Samet B. A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer Methods Partial Differential Equations. 2021;37:1250–1268. doi: 10.1002/num.2257. - DOI

[7] Mohammadi H., Kumar S., Rezapour S., Etemad S. A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals. 2021;144

[8] Mohammadi H., Kumar S., Rezapour S., Etemad S. A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals. 2021;144

[9] Solís-Pérez J.E., Gómez-Aguilar J.F. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals. 2018;14:175–185.

[10] Solís-Pérez J.E., Gómez-Aguilar J.F. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals. 2018;14:175–185.

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Numerical treatments for the optimal control of two types variable-order COVID-19 model

Affiliations

Numerical treatments for the optimal control of two types variable-order COVID-19 model

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

Similar articles

References

LinkOut - more resources

Full Text Sources