Ab-initio contrast estimation and denoising of cryo-EM images
- PMID: 35901641
- PMCID: PMC9392052
- DOI: 10.1016/j.cmpb.2022.107018
Ab-initio contrast estimation and denoising of cryo-EM images
Abstract
Background and objective: The contrast of cryo-EM images varies from one to another, primarily due to the uneven thickness of the ice layer. This contrast variation can affect the quality of 2-D class averaging, 3-D ab-initio modeling, and 3-D heterogeneity analysis. Contrast estimation is currently performed during 3-D iterative refinement. As a result, the estimates are not available at the earlier computational stages of class averaging and ab-initio modeling. This paper aims to solve the contrast estimation problem directly from the picked particle images in the ab-initio stage, without estimating the 3-D volume, image rotations, or class averages.
Methods: The key observation underlying our analysis is that the 2-D covariance matrix of the raw images is related to the covariance of the underlying clean images, the noise variance, and the contrast variability between images. We show that the contrast variability can be derived from the 2-D covariance matrix and we apply the existing Covariance Wiener Filtering (CWF) framework to estimate it. We also demonstrate a modification of CWF to estimate the contrast of individual images.
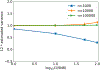
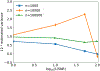
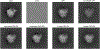
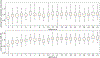
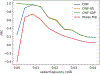
Results: Our method improves the contrast estimation by a large margin, compared to the previous CWF method. Its estimation accuracy is often comparable to that of an oracle that knows the ground truth covariance of the clean images. The more accurate contrast estimation also improves the quality of image restoration as demonstrated in both synthetic and experimental datasets.
Conclusions: This paper proposes an effective method for contrast estimation directly from noisy images without using any 3-D volume information. It enables contrast correction in the earlier stage of single particle analysis, and may improve the accuracy of downstream processing.
Keywords: Contrast estimation; Image denoising; Wiener filtering.
Copyright © 2022 Elsevier B.V. All rights reserved.
Figures

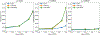
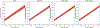
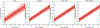
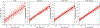
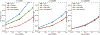

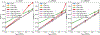

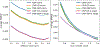

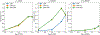
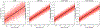
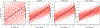
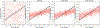
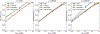
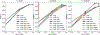

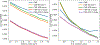



Similar articles
-
Denoising and covariance estimation of single particle cryo-EM images.J Struct Biol. 2016 Jul;195(1):72-81. doi: 10.1016/j.jsb.2016.04.013. Epub 2016 Apr 27. J Struct Biol. 2016. PMID: 27129418 Free PMC article.
-
Noise-Transfer2Clean: denoising cryo-EM images based on noise modeling and transfer.Bioinformatics. 2022 Mar 28;38(7):2022-2029. doi: 10.1093/bioinformatics/btac052. Bioinformatics. 2022. PMID: 35134862 Free PMC article.
-
A Fast Image Alignment Approach for 2D Classification of Cryo-EM Images Using Spectral Clustering.Curr Issues Mol Biol. 2021 Oct 18;43(3):1652-1668. doi: 10.3390/cimb43030117. Curr Issues Mol Biol. 2021. PMID: 34698131 Free PMC article.
-
AutoCryoPicker: an unsupervised learning approach for fully automated single particle picking in Cryo-EM images.BMC Bioinformatics. 2019 Jun 13;20(1):326. doi: 10.1186/s12859-019-2926-y. BMC Bioinformatics. 2019. PMID: 31195977 Free PMC article.
-
It's noisy out there! A review of denoising techniques in cryo-electron tomography.J Struct Biol. 2021 Dec;213(4):107804. doi: 10.1016/j.jsb.2021.107804. Epub 2021 Oct 31. J Struct Biol. 2021. PMID: 34732363 Review.
Cited by
-
Computational methods for in situ structural studies with cryogenic electron tomography.Front Cell Infect Microbiol. 2023 Oct 4;13:1135013. doi: 10.3389/fcimb.2023.1135013. eCollection 2023. Front Cell Infect Microbiol. 2023. PMID: 37868346 Free PMC article. Review.
-
Fast principal component analysis for cryo-electron microscopy images.Biol Imaging. 2023;3:e2. doi: 10.1017/s2633903x23000028. Epub 2023 Feb 3. Biol Imaging. 2023. PMID: 37645688 Free PMC article.
-
Cryo-EM Heterogeneity Analysis using Regularized Covariance Estimation and Kernel Regression.bioRxiv [Preprint]. 2024 Sep 6:2023.10.28.564422. doi: 10.1101/2023.10.28.564422. bioRxiv. 2024. PMID: 37961393 Free PMC article. Preprint.
References
-
- Bai X-C, McMullan G, Scheres SH, How cryo-EM is revolutionizing structural biology, Trends Biochem. Sci 40 (1) (2015) 49–57. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

