Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Jun 2;12(1):9206.
doi: 10.1038/s41598-022-13281-3.

A computational model of organism development and carcinogenesis resulting from cells' bioelectric properties and communication

Joao Carvalho  1
Affiliations

A computational model of organism development and carcinogenesis resulting from cells' bioelectric properties and communication

Joao Carvalho. Sci Rep. .

Abstract

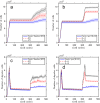
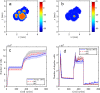
A sound theory of biological organization is clearly missing for a better interpretation of observational results and faster progress in understanding life complexity. The availability of such a theory represents a fundamental progress in explaining both normal and pathological organism development. The present work introduces a computational implementation of some principles of a theory of organism development, namely that the default state of cells is proliferation and motility, and includes the principle of variation and organization by closure of constraints. In the present model, the bioelectric context of cells and tissue is the field responsible for organization, as it regulates cell proliferation and the level of communication driving the system's evolution. Starting from a depolarized (proliferative) cell, the organism grows to a certain size, limited by the increasingly polarized state after successive proliferation events. The system reaches homeostasis, with a depolarized core (proliferative cells) surrounded by a rim of polarized cells (non-proliferative in this condition). This state is resilient to cell death (random or due to injure) and to limited depolarization (potentially carcinogenic) events. Carcinogenesis is introduced through a localized event (a spot of depolarized cells) or by random depolarization of cells in the tissue, which returns cells to their initial proliferative state. The normalization of the bioelectric condition can reverse this out-of-equilibrium state to a new homeostatic one. This simplified model of embryogenesis, tissue organization and carcinogenesis, based on non-excitable cells' bioelectric properties, can be made more realistic with the introduction of other components, like biochemical fields and mechanical interactions, which are fundamental for a more faithful representation of reality. However, even a simple model can give insight for new approaches in complex systems and suggest new experimental tests, focused in its predictions and interpreted under a new paradigm.

PubMed Disclaimer

Conflict of interest statement

The author declares no competing interests.

Figures

Figure 1
Figure 1
Standard simulation run. (a) Example of the final state of the system, with the color code showing the bioelectric state of each cell (membrane potential): a depolarized core surrounded by polarized cells, with a narrow transition border of cells with intermediate values of Vm (scale in mV). Each cell is represented by a 20μm size square pixel. (b) Evolution in time (in units of cell proliferation cycles) of the total number of cells (blue line) and the number of depolarized cells (dashed red line). At t≃40 cycles a fast transition to tissue polarization occurs (except for the depolarized core) and an approximately constant number of cells is reached (homeostasis). The bands show the standard deviation of the mean of n=25 simulation runs.
Figure 2
Figure 2
Wound healing test. (a) Example of a wound healing test, when about of 1/8 of the cells are removed after 300 cycles. (b) Ten cycles after the injury, cells from the depolarized core proliferate into the empty space, starting to fill it again. (c) After the test (t=500 cycles), the tissue recovered its shape and most of the lost cells. Color bar: cell membrane potential, in mV (white shows empty space).
Figure 3
Figure 3
Test of model parameters. (a) Change of cells death rate. (b) Variation of cells’ migration probability. (c) Shift of cell polarization rate after proliferation. The bands show the standard deviation of the mean of n=25 simulation runs.
Figure 4
Figure 4
Test of model parameters. (a) Change of cell variability level σ (standard deviation of the parameters’ central value). (b) Variation of the inter-cell communication level (gap junctions’ conductance). (c) Shift of initial cell bioelectric properties: high G0 means closer to the polarized state. The bands show the standard deviation of the mean of n=25 simulation runs.
Figure 5
Figure 5
Effect of a carcinogenic event. (a) Example of the tissue final state, after 500 cell cycles, ensuing from random depolarization of 40% of the cells at t=300 cell cycles, simulating a dispersed carcinogenic event, which increases the tissue size and the depolarized core. (b) Final state after a localized depolarized event, a circular depolarized spot, with radius R=20 cells, localized to the left of the central tissue region, at t=300 cell cycles. This depolarized spot drives tissue growth and gets merged with the initial depolarized core. Color bar: cell membrane potential, in mV (white shows empty space).
Figure 6
Figure 6
Tissue growth due to a carcinogenic event occurring at t=300 cell cycles. Total number of tissue cells as a function of cell cycles (a) and number of depolarized cells (c) for a dispersed event (random depolarization of a percentage of cells). Total number of tissue cells as a function of the number of cell cycles (b) and number of depolarized cells (d) for a localized event (depolarization of a spot with radius R, in number of cells). The bands show the standard deviation of the mean of n=25 simulation runs.
Figure 7
Figure 7
Tumor therapy. After the normal tissue growth, it suffers a dispersed carcinogenic event at t=300 cell cycles (random depolarization of 40% of the cells). The tumor grows and a diffuse therapeutic intervention is applied at t=500 cell cycles. (a) Tissue state at t=500 cells cycles, just before the therapy. (b) Tissue state at t=800 cell cycles (after the random depolarization of 60% of the cells), showing that almost all the tissue is polarized, therefore in a non-proliferative state. Color bar in (a,b): cell membrane potential, in mV (white shows empty space). Evolution in time of the total number of tissue cells (c) and depolarized cells (d) for three therapy levels (percentage of randomly repolarized cells). The bands in (c,d) show the standard deviation of the mean of n=25 simulation runs.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Gribbin GR. The Search for Superstrings, Symmetry, and the Theory of Everything. New York: Little Brown; 1999.
    1. Keynes JM. The General Theory of Employment. London: Interest and Money General. Macmillan & Co; 1936.
    1. Loeb, J. The organism as a whole: From a physicochemical viewpoint. G P Putnam’s Sons. 10.1037/13845-000 (1916).
    1. Miller JG. Living Systems. New York: McGraw-Hill; 1978.
    1. Rosen R. Life itself, a comprehensive inquiry into the nature, origin, and fabrication of life. USA: Columbia University Press; 1991.

Publication types