Power law in COVID-19 cases in China
- PMID: 35603042
- PMCID: PMC9115516
- DOI: 10.1111/rssa.12800
Power law in COVID-19 cases in China
Abstract
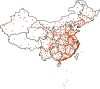
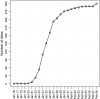
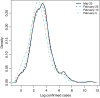
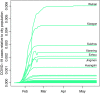
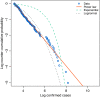
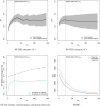
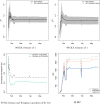
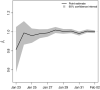
The novel coronavirus (COVID-19) was first identified in China in December 2019. Within a short period of time, the infectious disease has spread far and wide. This study focuses on the distribution of COVID-19 confirmed cases in China-the original epicentre of the outbreak. We show that the upper tail of COVID-19 cases in Chinese cities is well described by a power law distribution, with exponent around one in the early phases of the outbreak (when the number of cases was growing rapidly) and less than one thereafter. This finding is significant because it implies that (i) COVID-19 cases in China is heavy tailed and disperse; (ii) a few cities account for a disproportionate share of COVID-19 cases; and (iii) the distribution generally has no finite mean or variance. We find that a proportionate random growth model predicated by Gibrat's law offers a plausible explanation for the emergence of a power law in the distribution of COVID-19 cases in Chinese cities in the early phases of the outbreak.
Keywords: COVID‐19; Gibrat's law; Pareto distribution; coronavirus; heavy tailedness; power law; proportionate random growth.
© 2022 The Authors. Journal of the Royal Statistical Society: Series A (Statistics in Society) published by John Wiley & Sons Ltd on behalf of Royal Statistical Society.
Figures
Similar articles
-
On the emergence of a power law in the distribution of COVID-19 cases.Physica D. 2020 Nov;412:132649. doi: 10.1016/j.physd.2020.132649. Epub 2020 Jul 16. Physica D. 2020. PMID: 32834250 Free PMC article.
-
Quasi-Static Variation of Power-Law and Log-Normal Distributions of Urban Population.Entropy (Basel). 2021 Jul 17;23(7):908. doi: 10.3390/e23070908. Entropy (Basel). 2021. PMID: 34356449 Free PMC article.
-
Power-law distribution in the number of confirmed COVID-19 cases.Chaos. 2020 Sep;30(9):093123. doi: 10.1063/5.0013031. Chaos. 2020. PMID: 33003939 Free PMC article.
-
Spatial and Temporal Dimensions of Urban Expansion in China.Environ Sci Technol. 2015 Aug 18;49(16):9600-9. doi: 10.1021/acs.est.5b00065. Epub 2015 Aug 3. Environ Sci Technol. 2015. PMID: 26212783
-
The Coronavirus Disease 2019 (COVID-19) Pandemic.Tohoku J Exp Med. 2020 Apr;250(4):271-278. doi: 10.1620/tjem.250.271. Tohoku J Exp Med. 2020. PMID: 32321874 Review.
Cited by
-
The impact of a power law-induced memory effect on the SARS-CoV-2 transmission.Chaos Solitons Fractals. 2022 Dec;165:112790. doi: 10.1016/j.chaos.2022.112790. Epub 2022 Oct 25. Chaos Solitons Fractals. 2022. PMID: 36312209 Free PMC article.
-
Risk perception and oil and gasoline markets under COVID-19.J Econ Bus. 2021 May-Jun;115:105979. doi: 10.1016/j.jeconbus.2020.105979. Epub 2021 Jan 4. J Econ Bus. 2021. PMID: 33518846 Free PMC article.
-
The distribution of COVID-19 mortality.Infect Dis Model. 2022 Dec;7(4):856-873. doi: 10.1016/j.idm.2022.11.003. Epub 2022 Nov 19. Infect Dis Model. 2022. PMID: 36438695 Free PMC article.
-
Heavy-tailed distributions of confirmed COVID-19 cases and deaths in spatiotemporal space.PLoS One. 2023 Nov 21;18(11):e0294445. doi: 10.1371/journal.pone.0294445. eCollection 2023. PLoS One. 2023. PMID: 37988387 Free PMC article.
-
Time series analysis and short-term forecasting of monkeypox outbreak trends in the 10 major affected countries.BMC Infect Dis. 2024 Jan 2;24(1):16. doi: 10.1186/s12879-023-08879-5. BMC Infect Dis. 2024. PMID: 38166831 Free PMC article.
References
-
- Ahundjanov, B.B. & Akhundjanov, S.B. (2019) Gibrat's law for CO2 emissions. Physica A: Statistical Mechanics and its Applications, 526, 120944.
-
- Akhundjanov, S.B. & Chamberlain, L. (2019) The power law distribution of agricultural land size. Journal of Applied Statistics, 46(16), 3044–3056.
-
- Akhundjanov, S.B. & Drugova, T. (2021) On the growth process of U.S. agricultural land. Empirical Economics, in press.
-
- Akhundjanov, S.B. & Toda, A.A. (2020) Is Gibrat's ‘Economic Inequality’ lognormal? Empirical Economics, 59(5), 2071–2091.
-
- Akhundjanov, S.B. , Devadoss, S. & Luckstead, J. (2017) Size distribution of national CO2 emissions. Energy Economics, 66, 182–193.
LinkOut - more resources
Full Text Sources
