Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Sep 21;10(9):1151-1158.
doi: 10.1021/acsmacrolett.1c00500. Epub 2021 Sep 3.

Motor-Driven Restructuring of Cytoskeleton Composites Leads to Tunable Time-Varying Elasticity

Janet Y Sheung  1 , Daisy H Achiriloaie  1 , Christopher Currie  2 , Karthik Peddireddy  2 , Aaron Xie  1 , Jessalyn Simon-Parker  1 , Gloria Lee  2 , Michael J Rust  3 , Moumita Das  4 , Jennifer L Ross  5 , Rae M Robertson-Anderson  2
Affiliations

Motor-Driven Restructuring of Cytoskeleton Composites Leads to Tunable Time-Varying Elasticity

Janet Y Sheung et al. ACS Macro Lett. .

Abstract

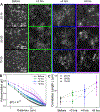
The composite cytoskeleton, comprising interacting networks of semiflexible actin and rigid microtubules, generates forces and restructures by using motor proteins such as myosins to enable key processes including cell motility and mitosis. Yet, how motor-driven activity alters the mechanics of cytoskeleton composites remains an open challenge. Here, we perform optical tweezers microrheology and confocal imaging of composites with varying actin-tubulin molar percentages (25-75, 50-50, and 75-25), driven by light-activated myosin II motors, to show that motor activity increases the elastic plateau modulus by over 2 orders of magnitude by active restructuring of both actin and microtubules that persists for hours after motor activation has ceased. Nonlinear microrheology measurements show that motor-driven restructuring increases the force response and stiffness and suppresses actin bending. The 50-50 composite exhibits the most dramatic mechanical response to motor activity due to the synergistic effects of added stiffness from the microtubules and sufficient motor substrate for pronounced activity.

PubMed Disclaimer

Conflict of interest statement

Notes

The authors declare no competing financial interest.

Figures

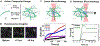
Figure 1.
Figure 1.
Optical tweezers microrheology characterizes how actomyosin activity alters the mechanical response of actin–microtubule composites. (A) Cartoon of composite composed of actin filaments, microtubules, and myosin II minifilaments, prepared as described in the Supporting Information. (B) 512 pixel × 512 pixel (213 μm × 213 μm) fluorescence confocal images of rhodamine-labeled microtubules in a 50–50 actin–tubulin composite acquired before, 2 h after, and 8 h after myosin activation. (C) Linear microrheology. (top) Cartoon depicting trapping a 4.5 μm diameter microsphere within a composite and tracking its force fluctuations (Fx, Fy) for 3 min. (bottom) Sample force magnitudes |F(t)|=(Fx2+Fy2)1/2 measured for the 50–50 composite before (black), during (red), and 4 h (blue) and 8 h (purple) after myosin activation. (D) Nonlinear microrheology. (top) Cartoon of measurement in which we hold an optically trapped bead fixed for 5 s, displace the bead 5 μm through the composite at 5 μm/s, and then hold it fixed again for the remaining of the 20 s measurement. We measure the force exerted on the microsphere for the duration of the measurement. Example force measurement for the 50–50 composite before (black) and 2 h after (green) 10 min of myosin activation. The gray curve shows the position of the piezoelectric stage that displaces the bead relative to the composite.
Figure 2.
Figure 2.
Myosin activity universally increases the elastic plateau of actin–microtubule composites with varying compositions. (A) Magnitude of the force exerted on optically trapped microspheres, |F(t)|=(Fx2+Fy2)1/2, embedded in composites of varying actin–tubulin molar percentages (listed in each panel) measured before (black) and during (red) 3 min of myosin activation as well as 4 h (blue) and 8 h (purple) after. Lighter dotted lines indicate individual trials, and darker solid lines indicate averages of the individual trials shown. The force exerted by the 50–50 composite at +4 h exceeded the strength of the optical trap for some trials, leading to the truncated force curves shown in the 50–50 plot. Arrows above the average force curve during activity indicate locations where the number of individual trials contributing to the average decreases due to truncated trials. (B) Elastic (G′(ω), closed symbols) and viscous (G″(ω), open symbols) moduli computed from the forces shown in (A). Color coding and panel organization is as in (A). The shaded region surrounding each curve indicates standard error. (C) Elastic plateau modulus GN0 determined from the data shown in (B). (D, E) Fast (τc1, D) and slow (τc2, E) relaxation times determined from the high (ωc1) and low (ωc2) frequencies at which G′(ω) and G″(ω) cross.
Figure 3.
Figure 3.
Myosin-driven restructuring increases the nonlinear force response and suppresses relaxation of actin–microtubule composites. (A) Average force F(x) exerted on the bead during nonlinear strain, measured before (black) and 2 h after (green) myosin activation, for composites with actin–tubulin percentages of 25–75 (left), 50–50 (middle), and 75–25 (right). Shaded regions along each curve indicate standard error. Insets: boxplots of differential modulus, K = dF/dx, found as the slope of F(x) for each trial. (B) Relaxation of force versus time following strain, measured before and 2 h after motor activation. Nearly all curves are well fit to a sum of two exponentials and a nonzero offset: F(t) = F∞ + C1e−t/τ1 + C2e−t/τ2. The 25–75 relaxation after activation fits to a single exponential. Fits are shown as red lines. (C) Time constants corresponding to fast (τ1, closed symbols) and slow (τ2, open symbols) modes determined from fits in (B) for relaxations measured before (black) and 2 h after (green) activation. The dashed line corresponds to predicted actin bending time scale τB, and the gray region corresponds to previously measured reptation times for steady-state composites. (D) Relative contributions of the fast (c1) and slow (c2) modes determined from the fits in (B). Dashed horizontal line indicates equal contribution from both modes. (E) F∞ determined from the fits shown in (B), corresponding to the force that is sustained at the end of the relaxation period.
Figure 4.
Figure 4.
Myosin activity drives sustained mesoscale clustering in actin–microtubule composites. (A) Representative 512 pixel × 512 pixel fluorescence confocal micrographs of rhodamine-labeled microtubules in actin–microtubule composites with actin–tubulin molar percentages of 25–75 (top), 50–50 (middle), and 75–25 (right). Images were acquired with 568 nm illumination at varying times relative to myosin activation: before (black) and 2 h (green), 4 h (blue), and 8 h (purple) after. (B) Average autocorrelation curves g(r), computed from five images for each time point, for the 50–50 composite. Error bars are standard error. Curves are fit to the equation shown to determine the correlation length ξ for each composite and time shown in panel C. (C) Average correlation lengths ξ for 25–75 (triangles), 50–50 (squares), and 75–25 (circles) composites at each time shown in (A).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Burla F; Mulla Y; Vos B; Aufderhorst-Roberts A; Koenderink G From Mechanical Resilience to Active Material Properties in Biopolymer Networks. Nat. Rev. Phys. 2019, 1, 249.
    1. Fletcher DA; Mullins RD Cell Mechanics and the Cytoskeleton. Nature 2010, 463 (7280), 485–492. - PMC - PubMed
    1. Forth S; Kapoor TM The Mechanics of Microtubule Networks in Cell Division. J. Cell Biol. 2017, 216 (6), 1525–1531. - PMC - PubMed
    1. Barlan K; Gelfand VI Microtubule-Based Transport and the Distribution, Tethering, and Organization of Organelles. Cold Spring Harbor Perspect. Biol 2017, 9 (5), a025817. - PMC - PubMed
    1. Blanchoin L; Boujemaa-Paterski R; Sykes C; Plastino J Actin Dynamics, Architecture, and Mechanics in Cell Motility. Physiol. Rev. 2014, 94 (1), 235–263. - PubMed

Publication types