Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Feb 15;27(4):1306.
doi: 10.3390/molecules27041306.

The Removal of Time-Concentration Data Points from Progress Curves Improves the Determination of Km: The Example of Paraoxonase 1

Boštjan Petrič  1 , Marko Goličnik  1 , Aljoša Bavec  1
Affiliations

The Removal of Time-Concentration Data Points from Progress Curves Improves the Determination of Km: The Example of Paraoxonase 1

Boštjan Petrič et al. Molecules. .

Abstract

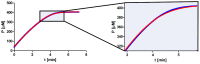
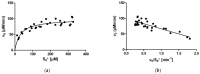
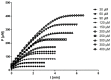
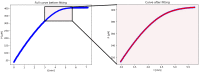
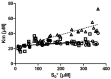
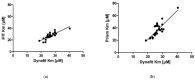
Several approaches for determining an enzyme's kinetic parameter Km (Michaelis constant) from progress curves have been developed in recent decades. In the present article, we compare different approaches on a set of experimental measurements of lactonase activity of paraoxonase 1 (PON1): (1) a differential-equation-based Michaelis-Menten (MM) reaction model in the program Dynafit; (2) an integrated MM rate equation, based on an approximation of the Lambert W function, in the program GraphPad Prism; (3) various techniques based on initial rates; and (4) the novel program "iFIT", based on a method that removes data points outside the area of maximum curvature from the progress curve, before analysis with the integrated MM rate equation. We concluded that the integrated MM rate equation alone does not determine kinetic parameters precisely enough; however, when coupled with a method that removes data points (e.g., iFIT), it is highly precise. The results of iFIT are comparable to the results of Dynafit and outperform those of the approach with initial rates or with fitting the entire progress curve in GraphPad Prism; however, iFIT is simpler to use and does not require inputting a reaction mechanism. Removing unnecessary points from progress curves and focusing on the area around the maximum curvature is highly advised for all researchers determining Km values from progress curves.

Keywords: Lambert W; dihydrocoumarin; integrated Michaelis–Menten equation; lactonase activity; paraoxonase 1; progress curves.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure A1
Figure A1
The integrated Michaelis–Menten equation being fitted in Prism to the same progress curve (blue line) that is shown in Figure 3. The model function (red line) appears to be a good fit for the progress curve. However, once we zoom into the area of maximum curvature, it is clear that the fit is no longer as good, which results in an erroneous Km value.
Figure 1
Figure 1
Determination of Km of rePON1 from the initial rates. (a) The Michaelis–Menten diagram: Km = 31 ± 6 µM. (b) The Eadie–Hofstee diagram: Km = 33 ± 4 µM, R = 0.84, R2 = 0.71. (c) The Woolf–Hanes diagram: Km = 34 ± 8 µM, R = 0.98, R2 = 0.95. (d) The Lineweaver–Burk diagram: Km = 35 ± 2 µM, R = 0.96, R2 = 0.93. The [S]0* are the initial substrate concentrations calculated from the progress curves.
Figure 1
Figure 1
Determination of Km of rePON1 from the initial rates. (a) The Michaelis–Menten diagram: Km = 31 ± 6 µM. (b) The Eadie–Hofstee diagram: Km = 33 ± 4 µM, R = 0.84, R2 = 0.71. (c) The Woolf–Hanes diagram: Km = 34 ± 8 µM, R = 0.98, R2 = 0.95. (d) The Lineweaver–Burk diagram: Km = 35 ± 2 µM, R = 0.96, R2 = 0.93. The [S]0* are the initial substrate concentrations calculated from the progress curves.
Figure 2
Figure 2
The fit of kinetic progress curve data at different substrate concentrations. Symbols represent absorbance readings converted into concentrations at the given reaction time. For clarity, only one progress curve per experiment and only 1/10 of the data points per progress curve are shown. Smooth lines represent least-square model curves generated by the fit of Equation (4) with the parameter values obtained by the modified model shown in Table 2 (Prism, entire curve). The concentrations shown on the right are the initially assumed ones; the actual (adjusted) concentrations in the cuvettes were calculated from the progress curves and used in all subsequent calculations. The 3rd parallel run is shown. The curves do not originate from the point (0,0); hence, the curves’ plateaus are higher than the S0* values displayed in Table 2.
Figure 3
Figure 3
The fit of kinetic progress curve data by iFIT. The entire curve is displayed on the (left), whereas only points from the area of highest curvature were included in the fit (right). The blue line represents absorbance readings converted into concentration at the given reaction time. Only one progress curve is shown, for clarity. The red line represents the least-square model curve generated by fitting with Equation (4) after the iteration process, with the parameter values obtained by the modified model shown in Table 2 (iFIT). The progress curve is the 400 µM curve from the 3rd parallel run shown in Figure 2 and Table 2.
Figure 4
Figure 4
The relationship between adjusted substrate concentration ([S]0*) and Km for Dynafit (circles), iFIT (squares), and Prism (the entire curve) (triangles) for all 30 measurements. Lines represent least-square model curves generated by a linear fit. The correlation coefficients and R-squared of the best-fit lines are R = 0.443 and R2 = 0.196 (iFIT), R = 0.525 and R2 = 0.276 (Dynafit), and R = 0.887 and R2 = 0.787 (Prism: the entire curve), respectively. The concentrations displayed were calculated retrospectively from the progress curves (Table 2).
Figure 5
Figure 5
The relationship between output Km values for the same progress curves analyzed by three different programs: (a) iFIT vs. Dynafit, (b) Prism (the entire curve) vs. Dynafit, and (c) Prism (the entire curve) vs. iFIT. On each graph, all Km calculations are shown. The linear fits of the relationships are as follows: (a) (iFIT Km) = 1.15 · (Dynafit Km) − 3.47 µM; (b) (Prism (the entire curve) Km) = 2.36 · (Dynafit Km) − 26.26 µM; and (c) (Prism (the entire curve) Km) = 1.36 · (iFIT Km) − 0.17 µM. The R and R2 values for all three comparisons are shown in (d).
Figure 5
Figure 5
The relationship between output Km values for the same progress curves analyzed by three different programs: (a) iFIT vs. Dynafit, (b) Prism (the entire curve) vs. Dynafit, and (c) Prism (the entire curve) vs. iFIT. On each graph, all Km calculations are shown. The linear fits of the relationships are as follows: (a) (iFIT Km) = 1.15 · (Dynafit Km) − 3.47 µM; (b) (Prism (the entire curve) Km) = 2.36 · (Dynafit Km) − 26.26 µM; and (c) (Prism (the entire curve) Km) = 1.36 · (iFIT Km) − 0.17 µM. The R and R2 values for all three comparisons are shown in (d).
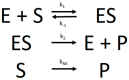
Figure 6
Figure 6
The Michaelis–Menten reaction scheme, with the nonenzymatic decay of substrate added in the bottom line. The formation of the enzyme–substrate complex is the “slow” step of the overall reaction, whereas the formation of product is the “fast” step. If k−1 = 0, the reaction proceeds according to the Van Slyke–Cullen mechanism.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Yun S.L., Suelter C.H. A simple method for calculating Km and V from a single enzyme reaction progress curve. BBA—Enzymol. 1977;480:1–13. doi: 10.1016/0005-2744(77)90315-1. - DOI - PubMed
    1. Duggleby R.G., Clarke R.B. Experimental designs for estimating the parameters of the Michaelis-Menten equation from progress curves of enzyme-catalyzed reactions. Biochim. Biophys. Acta (BBA)—Protein Struct. Mol. Enzymol. 1991;1080:231–236. doi: 10.1016/0167-4838(91)90007-M. - DOI - PubMed
    1. Schnell S., Mendoza C. Closed Form Solution for Time-dependent Enzyme Kinetics. J. Theor. Biol. 1997;187:207–212. doi: 10.1006/jtbi.1997.0425. - DOI
    1. Goličnik M. On the Lambert W function and its utility in biochemical kinetics. Biochem. Eng. J. 2012;63:116–123. doi: 10.1016/j.bej.2012.01.010. - DOI
    1. Kuzmič P. Program DYNAFIT for the Analysis of Enzyme Kinetic Data: Application to HIV Proteinase. Anal. Biochem. 1996;237:260–273. doi: 10.1006/abio.1996.0238. - DOI - PubMed

Substances

LinkOut - more resources