Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Jun;18(179):20210146.
doi: 10.1098/rsif.2021.0146. Epub 2021 Jun 16.

Is the diatom sex clock a clock?

Thomas Fuhrmann-Lieker  1 , Nico Kubetschek  1 , Jonas Ziebarth  1 , Roland Klassen  2 , Werner Seiler  3
Affiliations

Is the diatom sex clock a clock?

Thomas Fuhrmann-Lieker et al. J R Soc Interface. 2021 Jun.

Abstract

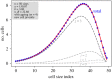
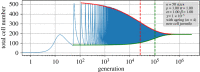
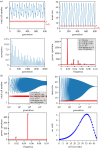
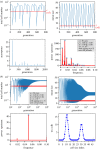
The unique life cycle of diatoms with continuous decreasing and restoration of the cell size leads to periodic fluctuations in cell size distribution and has been regarded as a multi-annual clock. To understand the long-term behaviour of a population analytically, generic mathematical models are investigated algebraically and numerically for their capability to describe periodic oscillations. Whereas the generally accepted simple concepts for the proliferation dynamics do not sustain oscillating behaviour owing to broadening of the size distribution, simulations show that a proposed limited lifetime of a newly synthesized cell wall slows down the relaxation towards a time-invariant equilibrium state to the order of a hundred thousand generations. In combination with seasonal perturbation events, the proliferation scheme with limited lifetime is able to explain long-lasting rhythms that are characteristic for diatom population dynamics. The life cycle thus resembles a pendulum clock that has to be wound up from time to time by seasonal perturbations rather than an oscillator represented by a limit cycle.

Keywords: clocks; diatoms; discrete models; matrix models; oscillations.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Three different models for the proliferation mechanism of diatoms: (a) simple binary fission (basic linear model) and (b) binary fission with a delay of one generation for the hypothecal daughter (Müller delay model). (c) Binary fission with a delay of one generation for the epithecal daughter (Laney delay model). Cells that cannot divide in the next generation are denoted with brackets. The total number of cells is counted in the columns on the right-hand side (grey numbers).
Figure 2.
Figure 2.
Results of the linear model with parameters near to a true steady state, characterized by a constant total cell number (per unit volume) as well as a constant population distribution.
Figure 3.
Figure 3.
Results of a nonlinear Ricker model with a value for p exceeding the critical value for the first bifurcation. It can be seen that the high-frequency oscillation in the population (period 2) does not couple to the generation cycle (period around n).
Figure 4.
Figure 4.
Age treatment of auxospores. i represents the size class and j the age. They retain their age or are set to pristine again (arrow). The 4 sizes × 3 ages model, starting with the third generation. The narrowing distribution is indicated in the columns to the right of the matrices.
Figure 5.
Figure 5.
Results of a nonlinear ageing model in which auxospores carry a memory of the previous age.
Figure 6.
Figure 6.
Results of a nonlinear ageing model in which auxospores are always pristine. In the lower right plot, the trajectory has to be read counterclockwise.
Figure 7.
Figure 7.
Equilibrium distribution after 5.3 mio. generations for distinct age classes and summed over all ages, with corresponding β-binomial fitting functions. Simulation parameters are n = 50, m = 4, p = α = β = σ = 1, γ = 0.001.
Figure 8.
Figure 8.
Relaxation of the total cell number towards the equilibrium. Indicated are the enveloping stretched exponential fits for maxima and minima (thick solid lines) with the location of the inflection points (dashed lines). Note the logarithmic time scale. Simulation parameters are the same as in figure 7.
Figure 9.
Figure 9.
Simulation results for a system with sinusoidal variation of p down to 75% of its value, representing an annual zeitgeber. The nominal generation cycle (number of size classes) is n = 50 generations, the zeitgeber cycle z = 20 generations. (a) Behaviour at the beginning. Given is the total cell number, mean size, the auxospore number and the power spectrum of the total cell number. In both upper graphs, the sinusoidally varying value of p multiplied by a factor of 5 for better visibility is indicated as the bottom line in red. (b) Long-term behaviour. Replacing auxospore number, the size distribution after 106 generations is displayed.
Figure 10.
Figure 10.
Simulation results for a system with sinusoidal variation of s down to 75% of its value. Graphs are displayed as in figure 9 at the beginning (a) and for 106 generations (b).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Benoiston A-S, Ibarbalz FM, Bittner L, Guidi L, Jahn O, Dutkiewicz S, Bowler C. 2017. The evolution of diatoms and their biogeochemical functions. Phil. Trans. R. Soc. B 372, 20160397. (10.1098/rstb.2016.0397) - DOI - PMC - PubMed
    1. Tréguer P, et al. 2018 Influence of diatom diversity on the ocean biological carbon pump. Nat. Geosci. 11, 27-37. (10.1038/s41561-017-0028-x) - DOI
    1. Nelson DM, Tréguer P, Brzezinski MA, Leynaert A, Quéguiner B. 1995. Production and dissolution of biogenic silica in the ocean: revised global estimates, comparison with regional data and relationship to biogenic sedimentation. Global Biogeochem. Cycles 9, 359-372. (10.1029/95GB01070) - DOI
    1. Smayda TJ. 1997. What is a bloom? A commentary. Limnol. Oceanogr. 42, 1132-1136. (10.4319/lo.1997.42.5_part_2.1132) - DOI
    1. Platt T, White GN, Thai L, Sathyendranath S, Roy S. 2009. The phenology of phytoplankton blooms: ecosystem indicators from remote sensing. Ecol. Model. 220, 3057-3069. (10.1016/j.ecolmodel.2008.11.022) - DOI

Publication types

LinkOut - more resources