Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Apr 23;11(19):4969-4979.
doi: 10.1039/d0sc00480d.

Structure-mechanics statistical learning unravels the linkage between local rigidity and global flexibility in nucleic acids

Yi-Tsao Chen  1 , Haw Yang  2 , Jhih-Wei Chu  3
Affiliations

Structure-mechanics statistical learning unravels the linkage between local rigidity and global flexibility in nucleic acids

Yi-Tsao Chen et al. Chem Sci. .

Abstract

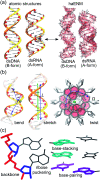
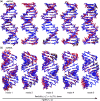
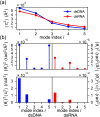
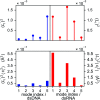
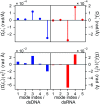
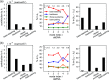
The mechanical properties of nucleic acids underlie biological processes ranging from genome packaging to gene expression, but tracing their molecular origin has been difficult due to the structural and chemical complexity. We posit that concepts from machine learning can help to tackle this long-standing challenge. Here, we demonstrate the feasibility and advantage of this strategy through developing a structure-mechanics statistical learning scheme to elucidate how local rigidity in double-stranded (ds)DNA and dsRNA may lead to their global flexibility in bend, stretch, and twist. Specifically, the mechanical parameters in a heavy-atom elastic network model are computed from the trajectory data of all-atom molecular dynamics simulation. The results show that the inter-atomic springs for backbone and ribose puckering in dsRNA are stronger than those in dsDNA, but are similar in strengths for base-stacking and base-pairing. Our analysis shows that the experimental observation of dsDNA being easier to bend but harder to stretch than dsRNA comes mostly from the respective B- and A-form topologies. The computationally resolved composition of local rigidity indicates that the flexibility of both nucleic acids is mostly due to base-stacking. But for properties like twist-stretch coupling, backbone springs are shown to play a major role instead. The quantitative connection between local rigidity and global flexibility sets foundation for understanding how local binding and chemical modification of genetic materials effectuate longer-ranged regulatory signals.

PubMed Disclaimer

Conflict of interest statement

There are no conflicts to declare statement.

Figures

Fig. 1
Fig. 1. Global flexibility and local rigidity in nucleic acids. (a) Atomic structures of B-form dsDNA and A-form dsRNA. All-atom MD simulations in explicit solvent are employed to compute an elastic network model of heavy atoms, haENM, to link local rigidity with global flexibility in nucleic acids. Local rigidity is represented as spring constants in haENM. (b) Order parameters like bending angle θ, contour length L, and twist angle Ω can be defined to describe the global shape of a linear polymer. (c) Local rigidity as spring constants in haENM can be categorized in terms of chemical interactions such as backbone, ribose puckering, base-stacking, and base-pairing.
Fig. 2
Fig. 2. Local rigidity in dsDNA and dsRNA. According to the atom typing on top-left, the springs are categorized into four groups, backbone, ribose puckering, base-stacking, and base-pairing. For the sub-groups in a category, a few springs are shown to illustrate the kind of connections in the structure. A larger integer in a sub-group name indicates longer equilibrium lengths, Fig. S2. The average and standard deviation of spring constants in each sub-group in kcal mol−1 Å−2 are listed to indicate the strengths of local rigidity.
Fig. 3
Fig. 3. The first five vibrational modes of (a) dsDNA and (b) dsRNA via quasi-harmonic analysis of the 1 μs all-atom MD trajectories. The modes are arranged in ascending order of eigenvalue and hence descending order of flexibility. Comparing mode 1 of dsDNA and dsRNA, the former is more relevant to bending and latter is more pronounced in stretching (Movies S1 and S2 in ESI†). Mode 3 and mode 5 of dsDNA contribute most to its twist flexibility and twist-stretch coupling, while such roles are played by mode 3 and mode 4 of dsRNA. More of these results are discussed later.
Fig. 4
Fig. 4. For bending angle flexibility σθ2 of dsDNA and dsRNA in all-atom MD simulations, the contribution from the first five vibrational modes. (a) The flexibility 〈ci2〉 of vibrational mode i. (b) Top panel: the square of the vector derivative of bending angle with respect to vibrational mode i, . Bottom panel: the contribution of vibrational mode i to bending angle flexibility, .
Fig. 5
Fig. 5. For contour length flexibility σL2 of dsDNA and dsRNA in all-atom MD simulations, the contribution from the first five vibrational modes. Top panel: the square of the vector derivative of contour length with respect to vibrational mode i, . Bottom panel: the contribution of vibrational mode i to contour length flexibility, .
Fig. 6
Fig. 6. For twist-stretch coupling σΩL of dsDNA and dsRNA in all-atom MD simulations, the contribution from the first five vibrational modes. Top panel: the product of and of mode i, i.e., its twist-stretch coupling. Bottom panel: the contribution of vibrational mode i to σΩL, .
Fig. 7
Fig. 7. Compositions of local rigidity in the eigenvalues of vibrational modes for (a) dsDNA and (b) dsRNA. Local rigidity is categorized in terms of chemical interactions as base-stacking, backbone, ribose puckering, and base-pairing springs. The eigenvalue of mode i, λi, represents its mechanical strength. Left panel: the contribution of different spring groups to the lowest eigenvalue, λ1, in kcal mol−1 Å−2. Middle panel: the percentage of different spring groups in the eigenvalues of modes 1–5. The ratios of λi to λ1 are labelled to indicate the rising rigidity with mode index i. Right panel: the percentage of different spring groups in the eigenvalue difference between the dominant modes of twist-stretch coupling, (λ5 − λ3) for dsDNA and (λ4 − λ3) for dsRNA.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Schleif R. Annu. Rev. Biochem. 1992;61:199–223. doi: 10.1146/annurev.bi.61.070192.001215. - DOI - PubMed
    1. Conway A. B. Lynch T. W. Zhang Y. Fortin G. S. Fung C. W. Symington L. S. Rice P. A. Nat. Struct. Mol. Biol. 2004;11:791–796. doi: 10.1038/nsmb795. - DOI - PubMed
    1. Cozzarelli N. R. Cost G. J. Nöllmann M. Viard T. Stray J. E. Nat. Rev. Mol. Cell Biol. 2006;7:580–588. doi: 10.1038/nrm1982. - DOI - PubMed
    1. Yeeles J. T. P. van Aelst K. Dillingham M. S. Moreno-Herrero F. Mol. Cell. 2011;42:806–816. doi: 10.1016/j.molcel.2011.04.012. - DOI - PubMed
    1. Dong K. C. Berger J. M. Nature. 2007;450:1201–1205. doi: 10.1038/nature06396. - DOI - PubMed