Spots, stripes, and spiral waves in models for static and motile cells : GTPase patterns in cells

doi:10.1007/s00285-021-01550-0

. 2021 Mar 4;82(4):28.

doi: 10.1007/s00285-021-01550-0.

Spots, stripes, and spiral waves in models for static and motile cells : GTPase patterns in cells

Yue Liu^{1

2}, Elisabeth G Rens^{3

4}, Leah Edelstein-Keshet³

Affiliations

¹ Department of Mathematics, University of British Columbia, Vancouver, V6T 1Z2, BC, Canada. yue.liu@maths.ox.ac.uk.
² Mathematical Institute, University of Oxford, Oxford, OX2 6GG, UK. yue.liu@maths.ox.ac.uk.
³ Department of Mathematics, University of British Columbia, Vancouver, V6T 1Z2, BC, Canada.
⁴ Delft Institute of Applied Mathematics, Delft University of Technology, Delft, The Netherlands.

PMID: 33660145
PMCID: PMC7929972
DOI: 10.1007/s00285-021-01550-0

Spots, stripes, and spiral waves in models for static and motile cells : GTPase patterns in cells

Yue Liu et al. J Math Biol. 2021.

. 2021 Mar 4;82(4):28.

doi: 10.1007/s00285-021-01550-0.

Authors

Yue Liu^{1

2}, Elisabeth G Rens^{3

4}, Leah Edelstein-Keshet³

Affiliations

¹ Department of Mathematics, University of British Columbia, Vancouver, V6T 1Z2, BC, Canada. yue.liu@maths.ox.ac.uk.
² Mathematical Institute, University of Oxford, Oxford, OX2 6GG, UK. yue.liu@maths.ox.ac.uk.
³ Department of Mathematics, University of British Columbia, Vancouver, V6T 1Z2, BC, Canada.
⁴ Delft Institute of Applied Mathematics, Delft University of Technology, Delft, The Netherlands.

PMID: 33660145
PMCID: PMC7929972
DOI: 10.1007/s00285-021-01550-0

Abstract

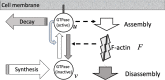
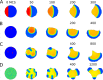
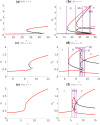
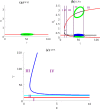
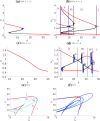
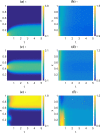
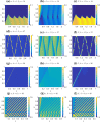
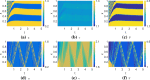
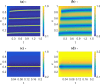
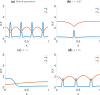
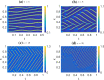
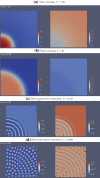
The polarization and motility of eukaryotic cells depends on assembly and contraction of the actin cytoskeleton and its regulation by proteins called GTPases. The activity of GTPases causes assembly of filamentous actin (by GTPases Cdc42, Rac), resulting in protrusion of the cell edge. Mathematical models for GTPase dynamics address the spontaneous formation of patterns and nonuniform spatial distributions of such proteins in the cell. Here we revisit the wave-pinning model for GTPase-induced cell polarization, together with a number of extensions proposed in the literature. These include introduction of sources and sinks of active and inactive GTPase (by the group of A. Champneys), and negative feedback from F-actin to GTPase activity. We discuss these extensions singly and in combination, in 1D, and 2D static domains. We then show how the patterns that form (spots, waves, and spirals) interact with cell boundaries to create a variety of interesting and dynamic cell shapes and motion.

Keywords: GTPase; Intracellular signaling; Local perturbation analysis; Pattern formation; Static and moving boundary computation; wave-pinning.

PubMed Disclaimer

Figures

**Fig. 1**
Schematic diagram of the models. The original wave-pinning model consists of GTPase (circles) in the active, (membrane-bound) form, u and inactive form v, with positive feedback (curved grey arrow) from u to its own activation (upwards white arrow), forming a positive feedback loop. The F-actin extension model (Holmes et al. 2012a) includes GTPase activation of F-actin assembly and GTPase inactivation by F-actin (dashed arrow), forming a negative feedback loop. The source-sink (nonconservative) extension by Verschueren and Champneys (2017) includes removal of active GTPase and synthesis of inactive GTPase so that the total amount is no longer conserved

**Fig. 2**
Time sequence (left to right) of u(x, y, t) in 2D simulations of the original wave pinning model (Eq. (1)a, b with $s = 0, c = 0$ . The circular domain is static, with no-flux boundary conditions and various initial conditions a–d but the same total amount w (see Eq. (3)). a stripe of high u (red) on the left, b randomly placed peak of u, c four random peaks, d uniform random noise. Sequence shows $t = 0, 50, 100$ MCS and a later steady state profile. a reaches steady state fastest. c and d take longer as multiple domains have to merge. Ultimately all cases result in a pinned wave at various locations along the cell edge. Parameters are from Table 4 (WP) except $δ = 0.1$ and $θ = 4.5$

**Fig. 3**
As in Fig. 2, but with boundary deformation that depends on u(x, y, t) at the cell edge. Here u represents the GTPase Rho, whose activity promotes retraction of the boundary into the domain. a, b The cell quickly polarizes (wavepinning of u) and then moves in a directed fashion (blue denotes low u at the front of the cell). c, d, edge retraction has trapped a plateau of u internally; this takes some time to resolve into a pinned wave in c or persists for a much longer time in (d). Parameters are as in Fig. 2, with CPM Parameters: $a = 10000$ , $λ_{a} = 0.02$ , $p = 400$ , $λ_{p} = 0.5$ , $J = 60$ , $r = 3, ξ (r) = 18$ , $β = 10$ , $T = 20$

**Fig. 4**
Bifurcation diagrams of the well-mixed (WM) and LPA wave pinning system with respect to the rate of activation parameter $γ$ . Other parameters as in Table 4 (WP) except w. The purple lines are located at bifurcation points separating the distinct regimes. Note that the “global branches” (curves in the WM diagrams) also appear in LPA, though their stability can be different in LPA over certain intervals. The numerical simulation associated with this system is presented in Fig. 9

**Fig. 5**
Two-parameter bifurcation plots of the wave pinning (WP) model with respect to parameters $w, γ$ . a Well-Mixed (WM) and b, c LPA system. Other parameters as in Table 4 (WP). Each curve in these diagrams traces the location of a bifurcation point shown in Fig. 4, and forms the boundary of a parameter regime. The one-parameter bifurcation diagrams in Fig. 4 correspond to vertical cross-sections of the diagrams here. The LPA regimes I - VII match with the regimes in Fig. 4(b, d, f). See summary in Table 1. c A zoom into the cusps in (b). (Compare (b) to LPA Fig. 3a of Holmes and Edelstein-Keshet (2016) for the same model with different parameter values: our figures agree on the (red) fold curves but ours includes an additional transcritical curve (light blue) separating several distinct regimes.)

**Fig. 6**
Bifurcation diagrams for the non-conservative (NC) model, with parameter values from Table 4 (CM2) except $η = 5$ . a WM, b, c LPA, using bifurcation parameters a, b $γ$ , with $c = 1$ , c c and $γ$ . A thin polarizable regime II is sandwiched between the stable I and Turing III regimes. In the full PDE simulations, which can be found in Figs. 12 and 13 , the triplet of Hopf bifurcations (not present in WP) does not show up as new behavior

**Fig. 7**
Bifurcation diagrams of the actin feedback (AF) model with respect to parameter s a–d and with respect to k, s in e ,f. (In e, the Hopf curves are omitted for clarity of the diagram. They are then included in f). The narrow regimes are not labelled. The nearly vertical blue curves indicate unstable periodic orbits. The associated simulations are presented in Fig. 10

**Fig. 8**
Same as Fig. 7f with the Hopf curves included, and with an indication of patterns in several regimes. A few Hopf curves lie very close to one of the other curves for most of their length, creating some very narrow regimes. The simulation results from Figs. 10 and 11 are identified with their corresponding regions on the parameter plane

**Fig. 9**
Simulation of the wave pinning model (WP), with parameters from Table 4 (WP). This parameter set corresponds to Regime IIIa as labelled in the bifurcation diagrams Fig. 4b and 5, which is classified as a polarizable regime. The patterns produced in the other polarizable regimes are qualitatively similar. Initial condition: $v = 1$ , $u = 0.102$ with perturbation $u = 6$ for (a ,b) $0 \leq x \leq 0.1$ ; (c ,d) $0.4 \leq x \leq 0.5$ ; (e ,f) random noise, $u = 0.834 \cdot ϵ (x)$ . Note that not all initial conditions result in wave pinning: a small perturbation from the HSS will simply decay and no pattern forms. The behaviors shown in a, b, e,f correspond to solutions shown in Fig. 2 of Mori et al. (2008)

**Fig. 10**
Simulations of the actin feedback model (AF) with parameters from Table 4 (AF) (s, k as indicated on labels), and default initial conditions. Each row corresponds to one parameters set, showing u, v, F (left to right). We also indicate the regimes each parameter set corresponds to in bifurcation diagram Figs. 7 and 8 . We observe four behaviors by varying k and s: a–c Wave pinning with oscillating front (WPO), within Regime IV but near the boundary with Regime VI; d–f Reflecting waves (RW), Regime IV; g–i Single pulse absorbed at boundary (SP), within Regime I but near the boundary of Regime IV; j–l Persistent wave trains (WT), Regime III. We used a larger domain length than Holmes et al. (2012a), leading to a richer set of patterns

**Fig. 11**
Exotic patterns observed in the actin feedback (AF) model. Parameters as in Table 4 (AF) but varying k, s. Both of these are located near regime boundaries in the bifurcation diagram Fig. 8. a–c $k = 5, s = 10$ , default initial conditions. The pattern resembles WPO but with several subregions; d–f $k = 5, s = 30$ , default initial conditions with excitation region $0 \leq x \leq 0.1$ . The resulting pattern is similar to RW but with a group of four pulses traversing the domain

**Fig. 12**
Simulation of the non-conservative model (NC) with a, b default parameters (Table 4 (NC)), corresponding to the unstable Regime III as identified in the bifurcation diagram Fig. 6; c, d $γ = 15 L^{2}, η = 15 L^{2}$ , which corresponds to the polarizable Regime II. Initial condition: a, b $u = u_{*}$ except $u = 1$ on $0 \leq x \leq 0.1$ , $v = v_{*}$ . c, d $u = u_{*} = 0.33333$ except $u = 10 u_{*}$ on $0.4 \leq x \leq 0.41$ , $v = v_{*} = 3.19298$ . In a, b, the formation of a peak on the left triggers some new peaks farther away, until space runs out. Once all peaks form, they shift slightly to be evenly spaced. In c, d, the single initial peak persists, without triggering new peaks. We refer to this as the soliton solution

**Fig. 13**
Final steady state pattern of the non-conservative model (NC) with most parameters from Table 4 (NC), except the parameters indicated on the labels. a and b correspond to the steady state of Fig. 12a, b and c, d respectively. In c the shortened domain results in wave pinning; d Higher inactivation rate $η = 15$ results in bifurcating peaks. a, b corresponds to Fig. 5a, d of Verschueren and Champneys (2017), respectively

**Fig. 14**
Simulations of the combined model (CM), where only the profiles of u are shown. The profiles of v show mostly similar patterns. Parameters as in Table 4 (CM2) but varying s, and HSS+noise initial condition as described in the text. As we increase the actin feedback strength s, the behavior transitions from slowly moving, repelling peaks to colliding peaks. At higher s, there is a rapidly oscillating standing wave pattern in some parts of the domain

**Fig. 15**
Simulations of the wave pinning a, b and non-conservative c, d models in a 2D static square domain, using the same parameters as in 1D (Table 4 (WP) and (NC)). Left: u , Right: v. For each model, two snap shots are shown: one when the pattern begin to take shape, and another after the system reached steady state

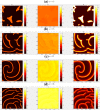
**Fig. 16**
2D simulations of the actin feedback (AF) model, with parameters from Table 4 (AF) and initial conditions described in the text. These snapshots are taken after the patterns have fully developed. As s increases, blobs transitions into thinner and thinner spiral waves. See movies at https://imgur.com/a/61GwiA9

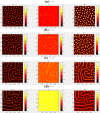
**Fig. 17**
Simulations of the combined model (CM) in 2D, with parameters from Table 4 (CM2) and HSS + noise initial condition. There is a transition from spots to spiral waves near $s = 12$ . See movies at https://imgur.com/a/a0u57GQ

**Fig. 18**
Snapshots of 2D CPM simulation with parameters from the absorbing waves in a static domain (AF model). Visualized is F-actin (F) that promotes protrusions ( $H_{0} = \pm β F$ ). Arrows indicate examples of interesting dynamics: (1) F-actin wave pushes membrane, (2)(a–c) A spot (2a) breaks into two waves (2b) and one wave changes direction (2c), (3a–c) a spiral starts to form. Snapshots are 20 MCS apart. Parameters are: $δ = 0.06$ , $L = 1$ , $k = 6$ , $s = 30$ , and the rest from Table 4 (AF). CPM Parameters are: $a = 12000$ , $λ_{a} = 2$ , $p = 500$ , $λ_{p} = 20$ , $J = 50$ , $r = 3, ξ (r) = 18$ , $β = 150$ , $T = 100$ . Movie link https://imgur.com/a/7OmgctR

**Fig. 19**
Snapshots of 2D CPM simulation with parameters from the oscillating waves in a static domain (AF model). Visualized is F-actin (F) that promotes protrusions ( $H_{0} = \pm β F$ ). Arrows indicate examples of interesting dynamics. (1)(a and b), a spot extends towards to membrane a and later breaks into two and one wave moves inwards b, (2) a wave creates a big protrusion, (3) a wave hits the cell edge and spirals in. Snapshots are 20 MCS apart. Parameters are as in Fig. 18, but with $k = 1.5$ , $s = 18$ . CPM parameters are as in Fig. 18, but with $β = 50$ . Movie link https://imgur.com/a/eIAjr59

**Fig. 20**
Snapshots of 2D CPM simulation with parameters from the reflecting waves in a static domain (AF model). Visualized is F-actin (F) that promotes protrusions ( $H_{0} = \pm β F$ ). Snapshots in A,B,C are 10,20,20 MCS apart respectively. Arrows indicate examples of interesting dynamics. a a wave hits a spot and breaks into two, b Two waves merge and change direction, c Part of a wave disappears as it encounters a spot. Parameters are as in Fig. 18, but with $k = 1.5$ , $s = 27$ . CPM parameters are as in Fig. 18, but with $β = 50$ . Movie link https://imgur.com/a/FDCn3NY

**Fig. 21**
Snapshots of 2D CPM simulation of the NC model. Visualized is Rac (u) that promotes protrusions ( $H_{0} = \pm β u$ ). Snapshots in A,B,C are 10,5,25 MCS apart respectively. Arrows indicate examples of interesting dynamics. a a spot breaks into two, b a new spot is created in a protrusion, c a spot leads a protrusion to form. Parameters are: $δ = 0.1$ , $η = 60$ , $k = 6$ , $γ = 120$ , $θ = 18$ , $α = 6$ , and the rest from Table 4 (NC). CPM Parameters are: $a = 10000$ , $λ_{a} = 0.02$ , $p = 1000$ , $λ_{p} = 0.04$ , $J = 40$ , $r = 3, ξ (r) = 18$ , $β = 200$ , $T = 20$ . Movie link https://imgur.com/yUUEgQD

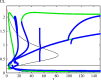
**Fig. 22**
LPA bifurcation diagram for the combined model (CM) with respect to the parameter s. Other parameters as in Table 4 (CM2). There are many apparent branches of periodic solutions. In a parameter range around $s = 20$ , there are no stable equilibria nor stable periodic solutions even though the system remains bounded, which suggests the presence of chaos

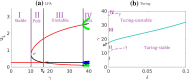
**Fig. 23**
Comparison of LPA and Turing bifurcation diagrams for the non-conservative model. a is a zoom of the LPA diagram from Fig. 6b. b is the Turing bifurcation diagram reproduced from Fig. 5 of Verschueren and Champneys (2017), using the same parameters. Observe that both the LPA-stable (I) and the LPA-polarizable (II) regimes in a located to the left of $γ_{c} = 16.765$ correspond to the Turing-stable regime below the blue curve in (b). The LPA-unstable regimes (III, IV) correspond to the Turing-unstable regime above the curve. The curve passes through $δ = 0, γ = γ_{c}$ . The bifurcation boundary between Regimes I and II, and between III and IV cannot be detected by Turing analysis. Given that numerical simulations have shown that the PDE produces the same behavior (Fig. 13a) in both Regimes III and IV, it is possible that these are not distinct regimes for the PDE. Overall, the LPA diagram (a) can be seen as a vertical slice of the Turing diagram b at $δ = 0$ , with additional bifurcation boundaries that separates the LPA-stable and LPA-polarizable regimes

**Fig. 24**
Simulations for the non-conservative model with random initial conditions $u = u_{*} (1 + Unif (- 0.01, + 0.01)), v = v_{*}$ with default parameters from Table 4 (NC) except $γ = 25$ . The color range is chosen so that the precursor pattern is more visible. The rapid transition from the shallower, higher frequency precursor pattern to the final pattern can be clearly seen

See this image and copyright information in PMC

Cited by

From actin waves to mechanism and back: How theory aids biological understanding.
Beta C, Edelstein-Keshet L, Gov N, Yochelis A. Beta C, et al. Elife. 2023 Jul 10;12:e87181. doi: 10.7554/eLife.87181. Elife. 2023. PMID: 37428017 Free PMC article.
Rho of Plants patterning: linking mathematical models and molecular diversity.
Deinum EE, Jacobs B. Deinum EE, et al. J Exp Bot. 2024 Feb 28;75(5):1274-1288. doi: 10.1093/jxb/erad447. J Exp Bot. 2024. PMID: 37962515 Free PMC article. Review.
Spatial models of pattern formation during phagocytosis.
Herron JC, Hu S, Liu B, Watanabe T, Hahn KM, Elston TC. Herron JC, et al. PLoS Comput Biol. 2022 Oct 3;18(10):e1010092. doi: 10.1371/journal.pcbi.1010092. eCollection 2022 Oct. PLoS Comput Biol. 2022. PMID: 36190993 Free PMC article.
Membrane Tension Can Enhance Adaptation to Maintain Polarity of Migrating Cells.
Zmurchok C, Collette J, Rajagopal V, Holmes WR. Zmurchok C, et al. Biophys J. 2020 Oct 20;119(8):1617-1629. doi: 10.1016/j.bpj.2020.08.035. Epub 2020 Sep 7. Biophys J. 2020. PMID: 32976760 Free PMC article.
On the influence of cell shape on dynamic reaction-diffusion polarization patterns.
Eroumé K, Vasilevich A, Vermeulen S, de Boer J, Carlier A. Eroumé K, et al. PLoS One. 2021 Mar 18;16(3):e0248293. doi: 10.1371/journal.pone.0248293. eCollection 2021. PLoS One. 2021. PMID: 33735291 Free PMC article.

See all "Cited by" articles

References

1. Alnaes MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. The FEniCS project version 1.5. Arch Numer Softw. 2015;3(100):9–23.
1. Bretschneider T, Anderson K, Ecke M, Müller-Taubenberger A, Schroth-Diez B, Ishikawa-Ankerhold HC, Gerisch G. The three-dimensional dynamics of actin waves, a model of cytoskeletal self-organization. Biophys J. 2009;96(7):2888–2900. doi: 10.1016/j.bpj.2008.12.3942. - DOI - PMC - PubMed
1. Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2019;82(2):1–33. - PubMed
1. Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2020;82(2):28. doi: 10.1007/s11538-020-00702-5. - DOI - PubMed
1. Champneys AR, Al Saadi F, Breña -Medina VF, Grieneisen VA, Marée AFM, Verschueren N, Wuyts B (2021) Bistability, wave pinning and localisation in natural reaction-diffusion systems. Phys D: Nonlinear Phenom 416(132735). 10.1016/j.physd.2020.132735

Publication types

Actions

MeSH terms

Actions
Actions
Actions
Actions
Actions
Actions

Substances

Actions

LinkOut - more resources

Full Text Sources
Other Literature Sources
- scite Smart Citations
Miscellaneous
- NCI CPTAC Assay Portal

[1] Alnaes MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. The FEniCS project version 1.5. Arch Numer Softw. 2015;3(100):9–23.

[2] Alnaes MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. The FEniCS project version 1.5. Arch Numer Softw. 2015;3(100):9–23.

[3] Bretschneider T, Anderson K, Ecke M, Müller-Taubenberger A, Schroth-Diez B, Ishikawa-Ankerhold HC, Gerisch G. The three-dimensional dynamics of actin waves, a model of cytoskeletal self-organization. Biophys J. 2009;96(7):2888–2900. doi: 10.1016/j.bpj.2008.12.3942. - DOI - PMC - PubMed

[4] Bretschneider T, Anderson K, Ecke M, Müller-Taubenberger A, Schroth-Diez B, Ishikawa-Ankerhold HC, Gerisch G. The three-dimensional dynamics of actin waves, a model of cytoskeletal self-organization. Biophys J. 2009;96(7):2888–2900. doi: 10.1016/j.bpj.2008.12.3942. - DOI - PMC - PubMed

[5] Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2019;82(2):1–33. - PubMed

[6] Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2019;82(2):1–33. - PubMed

[7] Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2020;82(2):28. doi: 10.1007/s11538-020-00702-5. - DOI - PubMed

[8] Buttenschön A, Liu Y, Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull Math Biol. 2020;82(2):28. doi: 10.1007/s11538-020-00702-5. - DOI - PubMed

[9] Champneys AR, Al Saadi F, Breña -Medina VF, Grieneisen VA, Marée AFM, Verschueren N, Wuyts B (2021) Bistability, wave pinning and localisation in natural reaction-diffusion systems. Phys D: Nonlinear Phenom 416(132735). 10.1016/j.physd.2020.132735

[10] Champneys AR, Al Saadi F, Breña -Medina VF, Grieneisen VA, Marée AFM, Verschueren N, Wuyts B (2021) Bistability, wave pinning and localisation in natural reaction-diffusion systems. Phys D: Nonlinear Phenom 416(132735). 10.1016/j.physd.2020.132735

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Spots, stripes, and spiral waves in models for static and motile cells : GTPase patterns in cells

Affiliations

Spots, stripes, and spiral waves in models for static and motile cells : GTPase patterns in cells

Authors

Affiliations

Abstract

Figures

Similar articles

Cited by

References

Publication types

MeSH terms

Substances

LinkOut - more resources

Full Text Sources

Other Literature Sources

Miscellaneous