Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Jan 19;34(3):108647.
doi: 10.1016/j.celrep.2020.108647.

Systematic alteration of in vitro metabolic environments reveals empirical growth relationships in cancer cell phenotypes

Karl Kochanowski  1 , Timur Sander  2 , Hannes Link  2 , Jeremy Chang  1 , Steven J Altschuler  3 , Lani F Wu  4
Affiliations

Systematic alteration of in vitro metabolic environments reveals empirical growth relationships in cancer cell phenotypes

Karl Kochanowski et al. Cell Rep. .

Abstract

Cancer cells, like microbes, live in complex metabolic environments. Recent evidence suggests that microbial behavior across metabolic environments is well described by simple empirical growth relationships, or growth laws. Do such empirical growth relationships also exist in cancer cells? To test this question, we develop a high-throughput approach to extract quantitative measurements of cancer cell behaviors in systematically altered metabolic environments. Using this approach, we examine relationships between growth and three frequently studied cancer phenotypes: drug-treatment survival, cell migration, and lactate overflow. Drug-treatment survival follows simple linear growth relationships, which differ quantitatively between chemotherapeutics and EGFR inhibition. Cell migration follows a weak grow-and-go growth relationship, with substantial deviation in some environments. Finally, lactate overflow is mostly decoupled from growth rate and is instead determined by the cells' ability to maintain high sugar uptake rates. Altogether, this work provides a quantitative approach for formulating empirical growth laws of cancer.

Keywords: cancer; growth law; metabolic environment; metabolism.

PubMed Disclaimer

Conflict of interest statement

Declaration of interests The authors declare no competing interests.

Figures

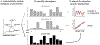
Figure 1.
Figure 1.
Schematic of approach to search for empirical growth relationships across metabolic environments
Figure 2.
Figure 2.. Experimental pipeline to cultivate cancer cells in multiple in vitro metabolic environments
(A) Schematic of the experimental pipeline. (B) Top row: cell number at 72 h (relative to 0 h) of PC9 cells upon amino acid depletion (diamonds) or replacement of glucose for alternative sugars (circles). Overall, >100 metabolic environments with unique nutrient composition were tested. Bottom row: corresponding maximal growth rate (relative to the reference condition). Error bars denote standard deviation (n = 2–3).
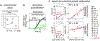
Figure 3.
Figure 3.. Divergent impacts of metabolic environments on chemotherapy and targeted therapy survival in PC9 cells
(A) Schematic of the experimental approach. (B) Example lethal fraction time courses highlighting the analytical approach to quantify drug survival. Black, reference condition. Green, fructose. Dashed lines denote standard deviation (n = 3). (C) Search for an empirical growth relationship for etoposide (top row) or erlotinib (bottom row). Left: delta AIC (ΔAIC) (compared with zero polynomial order) as a function of polynomial order. Black, original data. Gray, median of randomizing data labels 10,000 times. Red circle, polynomial order with minimal ΔAIC (= best fit). Right: death rate (relative to the reference condition) across metabolic environments plotted as a function of growth rate. Red line, best fit. Error bars denote standard deviation (n = 3).
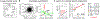
Figure 4.
Figure 4.. Impact of metabolic environments on cancer cell migration in PC9 cells follows a grow-and-go scheme
(A) Schematic of the experimental approach. (B) Example cell tracking data highlighting the analytical approach to quantify cell migration. Left: rose plot of individual tracks captured (with track number n) over 18 h in fructose. Each track was realigned to the origin. Right: corresponding distribution of average speed across tracks. Black, reference condition (all nutrients present at a concentration corresponding to standard RPMI 1640 media). Green, fructose. Shown are distributions of three separate replicates. Red dashed line, median of distribution across all replicates. (C) Search for an empirical growth relationship for cell migration. Left: ΔAIC (compared with zero polynomial order) as a function of polynomial order. Black, original data. Gray, median of randomizing data labels 10,000 times. Red circle, polynomial order with minimal ΔAIC (= best fit). Right: population speed (median of the average speed shown in B) plotted against the corresponding growth rate in 19 metabolic environments. Red line, best fit. Error bars denote standard deviation (n = 3).
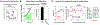
Figure 5.
Figure 5.. Lactate overflow is largely decoupled from growth rate across metabolic environments in PC9 cells
(A) Schematic of the experimental approach. (B) Example data highlighting the analytical approach to quantify the lactate secretion rate. Left: cell number time courses. Black, reference condition (glucose). Green, fructose. Right: corresponding produced lactate. (C) Search for an empirical growth relationship for the lactate secretion rate. Left: ΔAIC (compared with zero polynomial order) as a function of polynomial order. Red circle, polynomial order with minimal ΔAIC (= best fit). Right: lactate secretion rate as a function of growth rate relative to the reference condition (all nutrients present at a concentration corresponding to standard RPMI 1640 media) across metabolic environments in PC9 cells. Red line, best fit. Error bars denote standard deviation (n = 3).
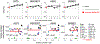
Figure 6.
Figure 6.. No simple empirical growth relationship accounts for lactate overflow across metabolic environments in diverse cell lines
Top row: ΔAIC (compared with zero polynomial order) as a function of polynomial order. Red circle, polynomial order with minimal ΔAIC (= best fit). Horizontal dashed line, ΔAIC cutoff of −3.22 (the respective model must be at least five times more likely than the null model; see STAR methods). Bottom row: lactate secretion rate as a function of growth rate relative to the reference condition (all nutrients present at a concentration corresponding to standard RPMI 1640 media) across metabolic environments. Red line, best fit. Error bars denote standard deviation (n = 3).
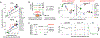
Figure 7.
Figure 7.. Investigating the source of variability in lactate secretion rate across metabolic environments
(A) Lactate overflow correlates strongly with sugar uptake rate. Lactate secretion rate plotted against sugar uptake rate across metabolic environments in PC9 cells (top) and A375 cells (bottom). Continuous black line, 1:1 molar relationship of lactate/sugar uptake. Dashed line, 2:1 molar relationship. Error bars denote standard deviation (n = 3). (B) Using metabolomics to examine potential sources for variation in lactate overflow. Left: schematic of mammalian sugar utilization and catabolism by oxidative phosphorylation or lactate fermentation. Boxed metabolites (e.g., G6P) denote hexose-phosphates (Hexose-Ps). Right: ratio of AMP/ATP relative to the reference condition and Hexose-P plotted against the corresponding lactate secretion rate (relative to the reference condition) in PC9 and A375 cells. Error bars denote standard deviation (n = 3). (C) Ability to increase lactate fermentation determines energetic response to complex I inhibition. ATP concentration (determined with CellTiterGlo, normalized to signal at t = 0 min) upon complex I inhibition with 1 μM rotenone in PC9 cells growing in conditions with high (glucose), intermediate (1:4 mannose [man]), or low (fructose [frc]) lactate secretion rates (indicative of the ability to increase lactate overflow if needed). Error bars denote standard deviation (n = 2).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Ahmadi M, Ahmadihosseini Z, Allison SJ, Begum S, Rockley K, Sadiq M, Chintamaneni S, Lokwani R, Hughes N, and Phillips RM (2014). Hypoxia modulates the activity of a series of clinically approved tyrosine kinase inhibitors. Br. J. Pharmacol 171, 224–236. - PMC - PubMed
    1. Ast T, and Mootha VK (2019). Oxygen and mammalian cell culture: are we repeating the experiment of Dr. Ox? Nat. Metab 1, 858–860. - PubMed
    1. Atkins RJ, Stylli SS, Kurganovs N, Mangiola S, Nowell CJ, Ware TM, Corcoran NM, Brown DV, Kaye AH, Morokoff A, et al. (2019). Cell quiescence correlates with enhanced glioblastoma cell invasion and cytotoxic resistance. Exp. Cell Res 374, 353–364. - PubMed
    1. Baguley BC, Marshall ES, Whittaker JR, Dotchin MC, Nixon J, McCrystal MR, Finlay GJ, Matthews JHL, Holdaway KM, and van Zijl P (1995). Resistance mechanisms determining the in vitro sensitivity to paclitaxel of tumour cells cultured from patients with ovarian cancer. Eur. J. Cancer 31A, 230–237. - PubMed
    1. Balaban NQ, Helaine S, Lewis K, Ackermann M, Aldridge B, Andersson DI, Brynildsen MP, Bumann D, Camilli A, Collins JJ, et al. (2019). Definitions and guidelines for research on antibiotic persistence. Nat. Rev. Microbiol 17, 441–448. - PMC - PubMed

Publication types