Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2020 Oct 14;21(20):7594.
doi: 10.3390/ijms21207594.

Membrane Curvature, Trans-Membrane Area Asymmetry, Budding, Fission and Organelle Geometry

Alexander A Mironov  1 , Anna Mironov  2 , Jure Derganc  3 , Galina V Beznoussenko  1
Affiliations
Review

Membrane Curvature, Trans-Membrane Area Asymmetry, Budding, Fission and Organelle Geometry

Alexander A Mironov et al. Int J Mol Sci. .

Abstract

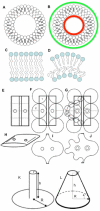
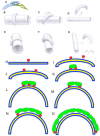
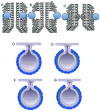
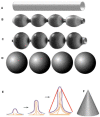
In biology, the modern scientific fashion is to mostly study proteins. Much less attention is paid to lipids. However, lipids themselves are extremely important for the formation and functioning of cellular membrane organelles. Here, the role of the geometry of the lipid bilayer in regulation of organelle shape is analyzed. It is proposed that during rapid shape transition, the number of lipid heads and their size (i.e., due to the change in lipid head charge) inside lipid leaflets modulates the geometrical properties of organelles, in particular their membrane curvature. Insertion of proteins into a lipid bilayer and the shape of protein trans-membrane domains also affect the trans-membrane asymmetry between surface areas of luminal and cytosol leaflets of the membrane. In the cases where lipid molecules with a specific shape are not predominant, the shape of lipids (cylindrical, conical, or wedge-like) is less important for the regulation of membrane curvature, due to the flexibility of their acyl chains and their high ability to diffuse.

Keywords: COP; Golgi; budding; caveola; endosome; filopodia; membrane fission; mitochondria fusion; nuclear envelope; trans–membrane area asymmetry.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Dependency of membrane curvature on different factors. (A,B) The role of sample preparation for the results of the measurement of membrane curvature. When the surface area of the leaflets is measured along the lipid head, the trans-membrane area asymmetry (TAA) of the vesicle will be 36/24 = 1.5, whereas if the surface area is measured along the external/internal border of the image visible after treatment with OsO4 (shown by green and red lines) TAA green/red will be 2.5. (C,D) Membrane bending affects the shape of acyl chains, but the lipid heads are stable. During bending the excess of lipid heads appears within the convex leaflet. (E–J) Undulation of the Golgi cisterna rims increases the cisterna TAA without significant change of its volume and surface area. Undulation could be large (F,I) and small (G,J). (K,L) Difference in the surface area between the filopodium and truncated cone. Filopodium (K): The length equals 2000 nm. The diameter of the filopodium equals 100 nm. The diameter of the plasmalemma surface area, used for the formation of the filopodium, is equal to 4000 nm. The surface area is equal to 1.82 × 107 nm2. Truncated cone (L): The diameter of the tip is equal to 100 nm. The height is equal to 2000 nm. The diameter of the plasmalemma surface area used for the filopodium formation is equal to 4000. The surface area is equal to 1.32 × 107 nm2 (R—radius of the plasmalemma area; r—radius of the tip and filopodium; h—height).
Figure 2
Figure 2
Role of the protein–membrane interactions in membrane curvature. (A) An example shape of a BAR domain. (B–G) Effect of BAR-like domains on membrane tubules and their interaction. Proteins containing BAR-like domains and other similar proteins are not highly bent. The TAA membrane curvature hypothesis suggests the following scenario. After attachment of such proteins to a rather thick membrane tubule, and insertion of part of the protein into the cytosolic leaflet of an endomembrane, proteins mostly orient perpendicularly to the long axis of the tube. Then the tubule becomes thinner, and this BAR-like domain reorients its position from a perpendicular to a more longitudinal one (F). Finally, the tubule becomes very thin and its curvature appears higher than the maximal curvature of the domain projection, even at a very small angle to the long axis of the tubule, (G) even when the orientation of this protein is at a very small angle related to the long axis of the tubules. As a result, this protein detaches from the membrane. This could lead to the excess of the luminal leaflet inducing the periplasmic fusion and fission of the tube at this site (see Figure 3). (H–O) A possible model of membrane budding induced by the membrane coat. (H) Insertion of a part of the one protein (red) into the lipid bilayer (blue) induces initial membrane bending. (I,J) Insertion of the second molecule of the first protein into the membrane increases its bending. (K) Connection of two first molecules by the second coat protein (green) makes this bending stable. (L) Insertion of the third molecule of the red protein, and then its attachment to the already formed coat, increases membrane bending. (M) After formation of a rather stable coat the middle molecule one of red proteins can detach. (M,N) Consecutive augmentation of the surface area of the rigid coat increases the curvature, and makes the coated membrane bud. This bud is attached to the membrane only near the edge of the coat (N). This coat is unstable and sensitive to the detachment of red proteins (see Figure 3).
Figure 3
Figure 3
The sudden elimination of coat proteins from the cytosolic leaflet of the lipid membrane can induce destabilization of a thin tubule, due to formation of protrusion of the luminal leaflet (A,B). Such a quick event induces formation of the excess of the luminal leaflet, and generation of the circular fold on the inner surface of the tube. This fold induces periplasmic fusion and fission of the tube at this site (C). (D–G) Possible model of vesicle fission. (D–G) Consecutive stages of the fission process. The coat is attached to the neck of the bud (D). The thinning of the bud neck induces detachment of red protein from the cytosolic leaflet (E). This induces periplasmic fusion and fission of the tube at this site (F,G).
Figure 4
Figure 4
Model describing the mechanism of transformation of a smooth tubule into a row of vesicles. (A–D) Consecutive stages of transformation of a cylinder into several spheres, with the preservation of surface area and TAA. When the surface area and TAA of a tubule is equal to the sum of the surface areas of the vesicles the radius of vesicle should be 2.2-fold higher than the radius of the cylinder (tubule). (E) Consecutive stages of the filopodia growth. The surface area of the cone (F) formed if the membrane was not attached to the actin bundle with ezrin, the surface area of the cone (red lines) would be larger than the surface area of the filopodia membrane and the ring of the plasmalemma around filopodia.
Figure 5
Figure 5
After mitochondria fusion the outer mitochondrial membrane becomes excessive. (A) Surface area of two ovoid figures before and after their fusion. Two half-spheres are excessive. (B–G) Stages of two consecutive mitochondria fusions. The fusion leads to the formation of excess of the surface area of the outer mitochondrial membrane, with the formation of the membrane protrusion (red arrow), which is then transformed into the multi-lamellar organelle (green arrow). Immediately after mitochondrial fusion the wall between the two mitochondria matrix compartments, derived from two mitochondria, is preserved (black arrows in F,G). (H) Example of long mitochondrion with such walls (black arrows). Thus, a mitochondrion formed after several consecutive fusions contains one or several partition walls (black arrows). Bar: 280 nm (H).
Figure 6
Figure 6
Caveolae and membrane geometry (A). (B) Low number of caveolae in an endothelial cell (EC) of the brain blood capillary. (A) Routine EM section. (B) Tomography virtual section. There are almost no caveolae. (C) Routine EM section of endothelial a cell of rat aorta after perfusion fixation. (D) Scanning EM (SEM) of the surface of endothelial cells (ECs) of rat aorta after perfusion fixation. The number of caveolae is low. (E) Routine longitudinal EM section of the aorta EC after immersion fixation. Many caveolae and their derivates are visible. (F) SEM of the rat aorta after immersion fixation. L-lumen of capillaries. Bars: 290 nm (A); 280 nm (B,C,E); 3 µm (D,F).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Singer S.J., Nicolson G.L. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. - DOI - PubMed
    1. Derganc J. Curvature-driven lateral segregation of membrane constituents in Golgi cisternae. Phys. Biol. 2007;4:317–324. doi: 10.1088/1478-3975/4/4/008. - DOI - PubMed
    1. Derganc J., Mironov A.A., Svetina S. The geometry of organelles of the secretory pathway. In: Mironov A.A., Pavelka M., editors. The Golgi Apparatus. Springer; Berlin/Heidelberg, Germany: 2008. pp. 314–330.
    1. Beznoussenko G.V., Pilyugin S.S., Geerts W.J., Kozlov M.M., Burger K.N., Luini A., Derganc J., Mironov A.A. Trans-membrane area asymmetry controls the shape of cellular organelles. Int. J. Mol. Sci. 2015;16:5299–5333. doi: 10.3390/ijms16035299. - DOI - PMC - PubMed
    1. Zimmerberg J., Kozlov M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. - DOI - PubMed

LinkOut - more resources