Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Oct 20;119(8):1617-1629.
doi: 10.1016/j.bpj.2020.08.035. Epub 2020 Sep 7.

Membrane Tension Can Enhance Adaptation to Maintain Polarity of Migrating Cells

Cole Zmurchok  1 , Jared Collette  2 , Vijay Rajagopal  2 , William R Holmes  3
Affiliations

Membrane Tension Can Enhance Adaptation to Maintain Polarity of Migrating Cells

Cole Zmurchok et al. Biophys J. .

Abstract

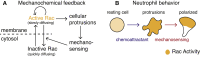
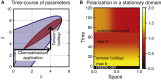
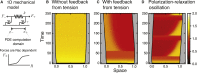
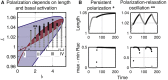
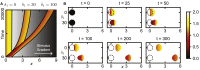
Migratory cells are known to adapt to environments that contain wide-ranging levels of chemoattractant. Although biochemical models of adaptation have been previously proposed, here, we discuss a different mechanism based on mechanosensing, in which the interaction between biochemical signaling and cell tension facilitates adaptation. We describe and analyze a model of mechanochemical-based adaptation coupling a mechanics-based physical model of cell tension coupled with the wave-pinning reaction-diffusion model for Rac GTPase activity. The mathematical analysis of this model, simulations of a simplified one-dimensional cell geometry, and two-dimensional finite element simulations of deforming cells reveal that as a cell protrudes under the influence of high stimulation levels, tension-mediated inhibition of Rac signaling causes the cell to polarize even when initially overstimulated. Specifically, tension-mediated inhibition of Rac activation, which has been experimentally observed in recent years, facilitates this adaptation by countering the high levels of environmental stimulation. These results demonstrate how tension-related mechanosensing may provide an alternative (and potentially complementary) mechanism for cell adaptation.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Overview of the mechanochemical feedback model and observed neutrophil behavior. (A) Schematic of mechanochemical feedback. Active (respectively inactive) Rac GTPases are assumed to be bound (respectively unbound) to the membrane and, therefore, slow (respectively fast) diffusing. Active Rac is autoactivated and causes cellular protrusions by activating downstream effectors. Cellular protrusions increase mechanosensing, which increases the deactivation rate of Rac. (B) Shown is a cartoon of the observed neutrophil behavior in a chemoattractive environment. A resting neutrophil is washed in chemoattractant, causing multiple sites of protrusive activity (within 20 s after stimulation). Subsequently, the cell adapts to the high signaling environment and polarizes to form a single leading front (∼60 s after stimulation). (B) is adapted from Fig. 3 B of (5) and the timescales are estimated from Fig. 2 A of (3). To see this figure in color, go online.
Figure 2
Figure 2
Parameter regimes of polar and nonpolar behavior and steady-state PDE solutions on a stationary domain. (A) The local perturbation analysis (LPA) reveals regimes of nonpolar (unshaded), stimulus-induced polarizable (blue shaded), and Turing unstable steady state, i.e., polarizable (red shaded), cell behavior in the bδ plane. The dots correspond to the parameters for steady-state Rac activity profiles in (B)–(E). (B–E) Shown are steady-state-simulated solutions to the PDEs. Initial conditions R(x, 0) = 0 except R(x, 0) = 5 for x > 0.9 are used in (B), (D), and (E). For (C), R(x, 0) = 1 + sin(4πx)/10 is used. Spatially homogeneous initial conditions were used for the inactive amount to ensure the total Rac (RT) is preserved: Ri(x,0)=RT−∫01R(x,0)dx. (B) Shown is the low Rac activity, b = 0.1 and δ = 7.5. (C) Shown is the polarized Rac activity, b = 0.1 and δ = 3. (D) Shown is the polarized Rac activity in the Turing regime, b = 4.5 and δ = 7.5. (E) Shown is the high Rac activity, b = 4.5 and δ = 3. The other parameters are D = 0.01, Di = 10, c = 5, n = 6, and RT = 2. To see this figure in color, go online.
Figure 3
Figure 3
Time-dependent parameters on a stationary domain mimic observed neutrophil behavior. (A) Shown is the trajectory of time-dependent parameters in the bδ plane mimicking uniform activation followed by increased tension-mediated inactivation. The shaded blue and red regions are the same as in Fig. 2A. Note that for a wide-range of parameter values, a change in δ (moving vertically across the bifurcation diagram) can push the cell into the polarizable or Turing regime in response to a change in chemoattractant levels, which modulate the activation of Rac through the parameter b (moving horizontally). (B) Shown is the kymograph of Rac activity in a stationary-domain simulation for these time-dependent parameters. The cell is at rest for t < 0 with b = 0.1 and δ = 3 (other parameters as in Fig. 2). For 0 < t < 5 (“max b”), the cell is stimulated with uniform chemoattractant b = 4 and jumps to the high Rac homogeneous steady state. For 5 < t < 50 (“tension buildup”), δ increases linearly in time: δ(t) = 3 + 4/45(t − 5) to reach a maximum of 7 at t = 50 (“max δ”). As a result of the increasing δ, the system re-polarizesdue to numerical error because the homogeneous steady state is linearly unstable with parameters in the Turing regime (“polarization onset”). See Video S1. To see this figure in color, go online.
Figure 4
Figure 4
1D mechanochemical model and tension-mediated cell polarization. (A) The cell is modeled as a 1D elastic spring (spring constant k) and viscous damping (damping constant γ). The PDEs are solved in the domain Ω(t) = [x−(t), x+(t)], which varies over time because of forces F± that depend on Rac activity at the cell ends (x±(t)). (B) Uniform stimulation leads to cell expansion without feedback from tension δ1 = 0. Black lines show x−(t) and x+(t), and color shows Rac activity. For this simulation, the cell is initialized at rest at time t = −5. The basal-activation rate parameter jumps from b = 0.1 to b = 4 at time t ≥ 0. Tension feeds back onto inactivation according to δ(T) = δ0 + δ1T, T = L(t) − ℓ0, δ0 = 3, and ℓ0 = 1. Other parameters are fR = 0.001, s1 = 10, s0 = 1, γ = 1, k = 0.01, c = 5, n = 6, RT = 2, D = 0.01, and Dii = 10. The initial conditions are R(x, 0) = 0.05645 and Ri(x, 0) = RT − 0.05645. See Video S2. (C) Uniform stimulation leads to cell expansion and polarization with feedback from tension δ1 = 80. Other parameters are as in (B). See Video S3. (D) With b = 2, uniform stimulation leads to indicate cyclical phases of polarization and relaxation. Other parameters and initial conditions are as in (C). See Video S4. To see this figure in color, go online.
Figure 5
Figure 5
Analysis of length dependence of dynamics. (A) LPA of the fixed domain system (L is thus a parameter, not a variable) reveals regimes of nonpolar (unshaded), stimulus-induced polarization (blue shaded region), and Turing instability (i.e., polarizable; inside the red shaded region) in the bL plane. Gray and black points illustrate length L trajectories from PDE simulations for various b-values. As the length changes because of Rac activity (dependent on mechanical parameters), the cell can be in a polarized (black) or nonpolar (gray) state. Once the cell’s length is in the Turing regime, polarization may occur. Regions I–IV denote the characteristic behavior for a range of b-values: I nonpolar, resting cells; II polarization-relaxation oscillation; III persistent polarization; and IV nonpolar, expanded cells. (B) Given are the plots of cell length (top row) and polarity strength (bottom row) for two example simulations of the coupled model in regimes III (b = 4; left column, labeled ∗ in A) and II (b = 2; right column, labeled ∗∗ in A), respectively. Top row: shown is the length as a function of time. Bottom row: shown is the difference between maximal and minimal Rac activity as a function of time (a proxy for polarization). Color indicates polar (black) or nonpolar (gray) Rac activity. To see this figure in color, go online.
Figure 6
Figure 6
Cell polarization in the 2D mechanochemical model. (A) Uniform stimulation leads to cell expansion without feedback from tension δ1 = 0. The dashed line indicates the cell’s initial position, and color corresponds to Rac activity. Here, δ depends on T as before: δ(T) = δ0 + δ1T; but tension is defined as the difference between this area and the rest area: T = A(t) − A0 with δ0 = 2 and A0 = 1. We apply a small internal chemoattractant gradient in the reference domain (i.e., in x¯-coordinates) to ensure polarization along the x-axis according to b(x¯) = b0 + b1x¯, with b0 = 4 and b1 = 0.1. The mechanical parameters are fR = 0.3 nN/μm, E = 0.3 kPa, ν = 0.45, γ = 20 kPa⋅s/μm2, and β = 10 s. The initial conditions are R(x, t) = 0, Ri(x, 0) = 2, with the mechanical system at rest (no displacement). See Video S5. (B) The cell is resting when exposed to chemoattractant at t = 0; it first expands uniformly and subsequently polarizes and migrates because of increased feedback from tension δ1 = 30. Other parameters are as in (A). See Video S6. (C) Shown is the predicted oscillatory behavior when not oversaturated with b0 = 2.0 and δ1 = 160. Other parameters are as in (A). See Video S7. See Fig. S5 for plots of cell area and polarity over time. To see this figure in color, go online.
Figure 7
Figure 7
Mechanosensing adaptation enables persistent migration in a chemoattractant gradient. Cells migrate up a chemoattractant gradient encoded in the basal-activation rate b(x) = b0 + b2x with b0 = 2.5 and b2 = 1. (A) 1D cells with feedback from tension (δ1 > 0) are able to migrate further up the chemoattractant gradient than those without feedback from tension (δ1 = 0) before becoming overstimulated and losing polarity (see also Figs. S5A and S6). (B) Snapshots over time of migrating cells in 2D without (top cell; δ1 = 0) and with (bottom cell; δ1 = 30) feedback from tension reveal the same behavior as in 1D (see also Fig. S7B). Shown are parameters as in Fig. 6, A and B except there is no longer an internal gradient applied to the interior of the cell in the stationary domain (b1 = 0). The dashed circle shows the initial position. See Videos S8 and S9. Color shows Rac activity in all panels. To see this figure in color, go online.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Zigmond S.H. Mechanisms of sensing chemical gradients by polymorphonuclear leukocytes. Nature. 1974;249:450–452. - PubMed
    1. Gardiner E.M., Pestonjamasp K.N., Bokoch G.M. Spatial and temporal analysis of Rac activation during live neutrophil chemotaxis. Curr. Biol. 2002;12:2029–2034. - PubMed
    1. Weiner O.D., Marganski W.A., Kirschner M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. - PMC - PubMed
    1. Houk A.R., Jilkine A., Weiner O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. - PMC - PubMed
    1. Saha S., Nagy T.L., Weiner O.D. Joining forces: crosstalk between biochemical signalling and physical forces orchestrates cellular polarity and dynamics. Philos. Trans. R Soc. Lond. B Biol. Sci. 2018;373:20170145. - PMC - PubMed

Publication types

LinkOut - more resources