Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Sep 1;117(35):21346-21353.
doi: 10.1073/pnas.2004091117. Epub 2020 Aug 17.

Talin folding as the tuning fork of cellular mechanotransduction

Rafael Tapia-Rojo  1 , Álvaro Alonso-Caballero  2 , Julio M Fernández  2
Affiliations

Talin folding as the tuning fork of cellular mechanotransduction

Rafael Tapia-Rojo et al. Proc Natl Acad Sci U S A. .

Abstract

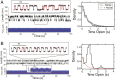
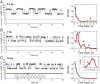
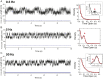
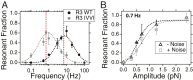
Cells continually sample their mechanical environment using exquisite force sensors such as talin, whose folding status triggers mechanotransduction pathways by recruiting binding partners. Mechanical signals in biology change quickly over time and are often embedded in noise; however, the mechanics of force-sensing proteins have only been tested using simple force protocols, such as constant or ramped forces. Here, using our magnetic tape head tweezers design, we measure the folding dynamics of single talin proteins in response to external mechanical noise and cyclic force perturbations. Our experiments demonstrate that talin filters out external mechanical noise but detects periodic force signals over a finely tuned frequency range. Hence, talin operates as a mechanical band-pass filter, able to read and interpret frequency-dependent mechanical information through its folding dynamics. We describe our observations in the context of stochastic resonance, which we propose as a mechanism by which mechanosensing proteins could respond accurately to force signals in the naturally noisy biological environment.

Keywords: magnetic tweezers; protein folding; stochastic resonance; talin.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

Fig. 1.
Fig. 1.
Mechanical characterization of the talin R3 domain. (A) Schematics of our magnetic tweezers assay for applying complex force signals to single proteins. Our construct contains the talin R3 domain followed by eight repeats of the titin I91 domain, flanked by a HaloTag for covalent anchoring to the glass surface and biotin for tethering with streptavidin-coated M-270 magnetic beads. Forces with a bandwidth greater than 10 kHz are generated using a magnetic tape head. (B) Typical single-molecule recording of talin R3 IVVI at 9 pN. (C) Typical recording of talin R3 WT at 5 pN. (Inset) Detail of the trajectory, highlighting the faster dynamics of R3 WT compared to the mutant R3 IVVI. Traces acquired at a frame rate between 1 kHz and 1.5 kHz and smoothed with a Savitzky–Golay fourth-order filter, with a 101-points box (R3 IVVI) and a 31-points box (R3 WT). (D) Folding probability of the R3 IVVI and R3 WT talin domains. The R3 IVVI mutant has a higher mechanical stability, and its folding probability is shifted to higher forces by 4 pN. (E) Folding (red) and unfolding (blue) rates for R3 IVVI (solid) and R3 WT (empty) talin domains. At the coexistence force, the rates of the WT are ∼12 s−1, compared to the slower ones of R3 IVVI (∼1.5 s−1). Data are fitted with the Bell–Evans model (dotted lines), yielding xF†=4.85±0.56 nm, k0F=(1.20±0.80)×105 s−1 and xU†=6.49±0.66 nm, k0U=(2.50±1.01)×10−3 s−1 for R3 WT, and xF†=6.78±0.59 nm, k0F=(1.84±1.01)×106 s−1 and xU†=4.27±0.34 nm, k0U=(4.61±2.52)×10−6 s−1 for R3 IVVI.
Fig. 2.
Fig. 2.
Talin detects oscillatory signals among mechanical noise. (A) (Left) Dynamics of the talin R3 IVVI domain under mechanical white noise with an average of 9 pN and an SD of 2.8 pN. (Inset) Detail of the trajectory with the idealized trace (red). (Right) Comparison of the dwell-time histograms in the unfolded state perturbed by a constant force of 9 pN (black) and external mechanical noise (gray). Both distributions are comparable, as talin remains insensitive to randomly fluctuating forces and responds only to the average perturbation. Histograms are built from 1,063 (no noise) and 704 transitions (noise). (B) (Left) Dynamics of the talin R3 IVVI domain perturbed by a force signal oscillating at 0.7 Hz, with an amplitude of 1 pN, and submerged in mechanical white noise with an SD of 2.8 pN. (Inset, Upper) Detailed of the idealized trace (red. (Inset, Lower) Detail of the force perturbation (red). (Right) Dwell-time histogram measured under such signal. The folding transitions are synchronized with the oscillating force, while the mechanical noise is ignored. These dynamics shift the shape of the dwell-time distribution, which shows resonance peaks at odd multiples of half of the period of the signal. The remnant stochastic behavior is appreciated as an underlying exponential distribution (red dotted line). Histogram is built with 2,295 transitions. Traces are acquired at a frame rate of 1–1.5 kHz, and smoothed with a Savitzky–Golay fourth-order algorithm with a 101-points box size.
Fig. 3.
Fig. 3.
Dynamics of the talin R3 IVVI domain under signals of different frequencies. (Left) The 50-s-long fragments of magnetic tweezers recordings showing R3 IVVI under a periodic signal with an amplitude of 0.7 pN, and frequencies of 0.1 (A), 1 (B), and 10 Hz (C). (Right) Dwell-time histograms on the unfolded state calculated for each of these signals. The interplay between the stochastic and resonant dynamics is manifested as a combination of exponential and Gaussian distributions, with relative weights that indicate the level of response (red fits). At 0.1 Hz (A), most transitions are stochastic, and only a small peak at 5 s appears (red asterisk). At 1 Hz (B), the response is optimal, and the majority of the histogram is built by Gaussian peaks, located at odd multiples of the half-period of the driving signal (red asterisk). At a high frequency of 10 Hz (C), the distribution is exponential, and only a logarithmic binning reveals a small proportion of resonant transitions at 0.05 s (Inset, red asterisk). Histograms are built with 223 (A), 337 (B), and 363 (C) transitions. Traces are acquired at a frame rate between 1 kHz and 1.5 kHz, and smoothed with a Savitzky–Golay fourth-order filter, with a 101-points box.
Fig. 4.
Fig. 4.
Response of the R3 WT domain under signals of different frequencies. (Left) The 10-s-long fragments of magnetic tweezers recordings showing R3 WT under a sinusoidal force signal with an amplitude of 0.7 pN, and frequencies of 0.5 (A), 5 (B), and 50 Hz (C), respectively. (Right) Dwell-time histograms on the unfolded state, for each of these signals. At 0.5 Hz (A) most transitions are stochastic, with a small entrained contribution appreciable in log-scale (Inset, red asterisk). At 5 Hz (B), the response is optimal and the dwell-time histogram has a major peaked contribution (red asterisk). At 50 Hz (C), the distribution is exponential, and only a minor entrained contribution is observed with logarithmic binning (Inset, red asterisk). Histograms are built with 715 (A), 2,736 (B), and 1,945 (C) transitions. Raw traces are shown, acquired at rates of 1 kHz to 1.5 kHz.
Fig. 5.
Fig. 5.
Quantitative characterization of the stochastic resonant dynamics by talin. (A) Fraction of resonant transitions for the R3 WT (black) and R3 IVVI (gray) domains. We characterize the level of resonant dynamics as the relative weight of the Gaussian-distributed transitions as measured from fits to the dwell-time distributions. Both domains show an optimal frequency range for signal detection around 10 Hz for R3 WT and 1 Hz for R3 IVVI. Higher frequencies are filtered, while lower ones show a majority of stochastic transitions due to the slow oscillation. Red dotted lines show the theoretical resonance frequency, based on the natural folding rates at the coexistence force. The histograms and fits used to determine FR are shown in SI Appendix, Figs. S6 and S7. (B) Fraction of resonant transitions as a function of the signal amplitude for a purely sinusoidal perturbation (black) and a sinusoid plus external mechanical noise (SD = 2.8 pN; gray), measured for R3 IVVI at f = 0.7 Hz. Dotted lines are sigmoidal fits to the data. Within statistical significance, there is no difference in talin response under either perturbation, which indicates that stochastic resonance is not affected by the addition of external mechanical noise to the coherent signal.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Eyckmans J., Boudou T., Yu X., Chen C. S., A hitchhiker’s guide to mechanobiology. Dev. Cell 21, 35–47 (2011). - PMC - PubMed
    1. Roca-Cusachs P., Conte V., Trepat X., Quantifying forces in cell biology. Nat. Cell Biol. 19, 742–751 (2017). - PubMed
    1. Yusko E. C., Asbury C. L., Force is a signal that cells cannot ignore. Mol. Biol. Cell 25, 3717–3725 (2014). - PMC - PubMed
    1. Orr A. W., Helmke B. P., Blackman B. R., Schwartz M. A., Mechanisms of mechanotransduction. Dev. Cell 10, 11–20 (2006). - PubMed
    1. Martino F., Perestrelo A. R., Vinarský V., Pagliari S., Forte G., Cellular mechanotransduction: From tension to function. Front. Physiol. 9, 824 (2018). - PMC - PubMed

Publication types

LinkOut - more resources