Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Nov:7:195.
doi: 10.3389/fphy.2019.00195. Epub 2019 Nov 29.

Strongly Bent Double-Stranded DNA: Reconciling Theory and Experiment

Aleksander V Drozdetski  1 , Abhishek Mukhopadhyay  1 , Alexey V Onufriev  1   2   3
Affiliations

Strongly Bent Double-Stranded DNA: Reconciling Theory and Experiment

Aleksander V Drozdetski et al. Front Phys. 2019 Nov.

Abstract

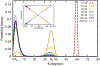
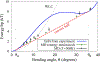
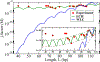
The strong bending of polymers is poorly understood. We propose a general quantitative framework of polymer bending that includes both the weak and strong bending regimes on the same footing, based on a single general physical principle. As the bending deformation increases beyond a certain (polymer-specific) point, the change in the convexity properties of the effective bending energy of the polymer makes the harmonic deformation energetically unfavorable: in this strong bending regime the energy of the polymer varies linearly with the average bending angle as the system follows the convex hull of the deformation energy function. For double-stranded DNA, the effective bending deformation energy becomes non-convex for bends greater than ~ 2° per base-pair, equivalent to the curvature of a closed circular loop of ~ 160 base pairs. A simple equation is derived for the polymer loop energy that covers both the weak and strong bending regimes. The theory shows quantitative agreement with recent DNA cyclization experiments on short DNA fragments, while maintaining the expected agreement with experiment in the weak bending regime. Counter-intuitively, cyclization probability (j-factor) of very short DNA loops is predicted to increase with decreasing loop length; the j-factor reaches its minimum for loops of ≃ 45 base pairs. Atomistic simulations reveal that the attractive component of the short-range Lennard-Jones interaction between the backbone atoms can explain the underlying non-convexity of the DNA effective bending energy, leading to the linear bending regime. Applicability of the theory to protein-DNA complexes, including the nucleosome, is discussed.

Keywords: DNA; convex hull; cyclization; deformation; j-factor; polymer bending.

PubMed Disclaimer

Conflict of interest statement

Conflict of Interest: The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Figures

FIGURE 1 |
FIGURE 1 |
Two different forms for a bending energy profile of a homopolymer. Shown is the (effective) bending energy per bending site E(θ). If the profile is purely convex down (black curve), the minimal energy conformations of the polymer is uniform bending (all sites are identically bent). If the function has a non-convex region (blue curve), non-uniform bending is more energetically favorable. In this case the total energy of the system follows the convex hull of the energy curve (red line).
FIGURE 2 |
FIGURE 2 |
Non-convex bending energy function leads to bi-modal distribution of bending angles. Shown are angular probability distributions at 300 K resulting from a realistic non-convex bending potential (Figure 4) used here in coarse-grained simulations of DNA closed loops of variable size. As the loop size (indicated in the top right corner) decreases, the average bending angle per base pair increases. When the average angle falls into the convex hull range, the angular distribution becomes bi-modal with peaks at θa and θb, corresponding to the weakly and strongly bent states, respectively. Fractional occupancy of both of these states of bending is shown in the inset as a function of the average bend angle θ¯. Squares: occupancy of the weakly bent state. Circles: occupancy of the strongly bent state, which can be interpreted as a “kink.” Out-of-plane motion likely affects angular probability distribution of the largest (600 bp) loop, which may explain the shift, compared to expectation, of the position of the corresponding distribution peak.
FIGURE 3 |
FIGURE 3 |
Examples of a 60- base-pair (left) and 80- base-pair (right) loop conformations at 300 K corresponding to the non-convex bending potential of Figure 4. The conformational ensembles were generated via coarse-grained simulations of DNA closed loops.
FIGURE 4 |
FIGURE 4 |
DNA effective bending energy E(θ) (per bp) extracted from the probability distribution [42] of DNA bends that naturally occur in protein-DNA complexes (blue line), and the average energy of unrestrained DNA closed loops simulated via coarse-grained MD with the same E(θ) (crosses). Green symbols: energy minimized (simulated annealing) loops. Black symbols: loops simulated at T=300K. In both cases, the average loop energy as a function of average bend angle θ¯=θ follows the convex hull of E(θ). The small deviation of the T = 300 K points from the convex hull are a result of ensemble average sampling and insignificant out-of-plane bending seen in the simulation.
FIGURE 5 |
FIGURE 5 |
DNA cyclization j-factors computed using the proposed ECH model (green line) and WLC (blue line) are compared with recent experiment [19] (red dots, L > 60 bp). Experimental values of persistence length, Lp = 150 bp and θa = 2.2° (Figure 4) were used; the value of k in Equation (6) was obtained independently for each model as best fit against two experimental data points for fragment length L = 101 and 106 bp (see Supplementary Material). The envelopes of the j-factor (brown dashed lines) for ECH and WLC are shown in the inset. Predicted envelope for ECH j-factor has a minimum near 45 bp. The experimental data points L = 50 and L = 40 bp were shared by Taekjip Ha (see reference [19]) in private communication to assess model performance after the model had been constructed.
FIGURE 6 |
FIGURE 6 |
The effective DNA bending energy, per base pair, as a function of the bending angle θ, inferred from all-atom MD simulations of uniformly bent DNA circles of variable lengths (50–400 bp). The statistical error bar is smaller than the symbol size. For reference, a WLC fit for small angle bends (up to≈ 3.5°, dashed line) is shown; the fit yields a persistence length of 58.2 nm (≈ 172 bp), reasonably close to the experimental value of ≈ 50 nm (≈ 150 bp).
FIGURE 7 |
FIGURE 7 |
Physical components of the (total) effective DNA bending energy from Figure 6. The original range of bend angles is reduced for clarity. The energies are per base pair, inferred from all-atom MD simulations of uniformly bent DNA circles of variable lengths (50–400 bp). The main contribution to the non-convexity of the bending energy comes from the Van der Waals (VDW) interactions. The backbone-backbone part of these interactions contribute the most to the non-convexity due to a sharp increase in the attractive energy component for 3° < θ < 4°, as shown in the inset. For reference, a WLC fit for the small angle bends (up to ≈ 3.5°, gray dashed line) is shown.
FIGURE 8 |
FIGURE 8 |
Polymer bending in a “protein-DNA complex” model with variable strength of polymer confinement and curvature (see “Methods”). The red circle represents the cylindrical charged core of the “protein” to which the oppositely charged “DNA” (black chain) is attracted. Under weak confinement, the system follows the convex hull of the effective E(θ), while approaching E(θ) (red dashed line) itself for strong confinement. Shown is the average energy per bead against the average bending angle θ, at different confinement strengths governed by the ratio |Q/qs| of the confining charge Q to the opposite charge qs of the confined polymer. The intrinsic bending of the polymer is described by (experimental) E(θ) from Figure 4.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Grosberg AY, Khokhlov AR, Jelinski LW. Giant molecules: here, there, and everywhere. Am J Phys. (1997) 65:1218–9.
    1. Garcia HG, Grayson P, Han L, Inamdar M, Kondev J, Nelson PC, et al. Biological consequences of tightly bent DNA: the other life of a macromolecular celebrity. Biopolymers. (2007) 85:115–30. doi: 10.1002/bip.20627 - DOI - PMC - PubMed
    1. Bustamante C, Chemla YR, Forde NR, Izhaky D. Mechanical processes in biochemistry. Annu. Rev. Biochem (2004) 73:705–48. doi: 10.1146/annurev.biochem.72.121801.161542 - DOI - PubMed
    1. Nelson P Transport of torsional stress in DNA. Proc Natl Acad Sci USA. (1999) 96:14342–7. - PMC - PubMed
    1. Van de Velde K, Kiekens P. Biopolymers: overview of several properties and consequences on their applications. Polym Test. (2002) 21:433–42. doi: 10.1016/S0142-9418(01)00107-6 - DOI

LinkOut - more resources