Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Apr 3;10(1):5919.
doi: 10.1038/s41598-020-62597-5.

Epidemics with mutating infectivity on small-world networks

Sten Rüdiger  1 , Anton Plietzsch  2   3 , Francesc Sagués  4 , Igor M Sokolov  2   5 , Jürgen Kurths  2   3   6
Affiliations

Epidemics with mutating infectivity on small-world networks

Sten Rüdiger et al. Sci Rep. .

Abstract

Epidemics and evolution of many pathogens occur on similar timescales so that their dynamics are often entangled. Here, in a first step to study this problem theoretically, we analyze mutating pathogens spreading on simple SIR networks with grid-like connectivity. We have in mind the spatial aspect of epidemics, which often advance on transport links between hosts or groups of hosts such as cities or countries. We focus on the case of mutations that enhance an agent's infection rate. We uncover that the small-world property, i.e., the presence of long-range connections, makes the network very vulnerable, supporting frequent supercritical mutations and bringing the network from disease extinction to full blown epidemic. For very large numbers of long-range links, however, the effect reverses and we find a reduced chance for large outbreaks. We study two cases, one with discrete number of mutational steps and one with a continuous genetic variable, and we analyze various scaling regimes. For the continuous case we derive a Fokker-Planck-like equation for the probability density and solve it for small numbers of shortcuts using the WKB approximation. Our analysis supports the claims that a potentiating mutation in the transmissibility might occur during an epidemic wave and not necessarily before its initiation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

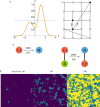
Figure 1
Figure 1
(a) Functional relation between the infection probability λ and the mutating variable γ. The dashed blue line shows the location of the percolation point for a square grid network of nodes. (b) Scheme showing the possible transitions during a time step. Every infected node recovers after a time step (left). A susceptible node that is linked to an infected node becomes infected with probability λ(γ), where γ is the genetic variable of the infected node. The infected node inherits the value γ that is then mutated to the new value γ′ in the same time step. (c) A two-dimensional square lattice where a fraction p of regular links has been replaced by long-distance links. Infections (filled circles) can travel to close neighbors but also to distant nodes. (d) Snapshots of the evolution of the γ variable on a network with 200 × 200 nodes for p = 0.01 and χ = 0.004 (blue - not infected, green - infected, γ = −1, yellow - infected with γ = 1). After 180 iterations the supercritical mutation covers almost all of the area.
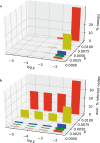
Figure 2
Figure 2
Epidemics of the SIR model with discrete mutations of the infection probability λd(γ) in a square lattice (N = 200 × 200) and a Watts-Strogatz-graph – dependence on two parameters: mutation rate χ and rewiring fraction p. (a) The z-axis is the share of runs in which almost complete coverage of the graph is obtained (number of R-nodes is larger than 90% at final state). (b) Share of R nodes averaged for 10,000 runs for each parameter set.
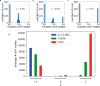
Figure 3
Figure 3
(a–c) Histograms showing the distribution of the number of R nodes in the final steady state per run for a total of 1,000 runs: χ = 0.001 (a), 0.004 (b), 0.01 (c). (d) Histogram of the γ variable (−1 or 1, no nodes reside in the 0 state in the final configuration) for the three values of mutation rate χ (p = 0.01).
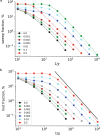
Figure 4
Figure 4
Discrete mutation model. (a) Percentage of sweeps in its dependence on χ (for indicated p values). (b) The same plot for the mutation probability. The solid line shows the slope of -2 for small χ.
Figure 5
Figure 5
Continuous mutation model. (a) Percentage of sweeps in its dependence on σ (for indicated p values), continuous case. (b) The same plot for the mutation probability. Dashed lines are linear fits. (c) A finite-size effect is visible at large p = 0.07 comparing a lattice of 300 by 300 points (black) compared to 200 by 200 points (green) and 100 by 100 points (brown) (for p = 0, 0.015 and 0.07, from bottom to top).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Dawood FS, et al. Estimated global mortality associated with the first 12 months of 2009 pandemic influenza A H1N1 virus circulation: a modelling study. The Lancet infectious diseases. 2012;12:687. doi: 10.1016/S1473-3099(12)70121-4. - DOI - PubMed
    1. WHO: Ebola situation report 30 March 2016 (2016).
    1. Danon, L. et al. Networks and the epidemiology of infectious disease. 2011 (2011). - PMC - PubMed
    1. Moore C, Newman ME. Epidemics and percolation in small-world networks. Physical Review E. 61. 2000;5:5678. doi: 10.1103/PhysRevE.61.5678. - DOI - PubMed
    1. Sander L, Warren C, Sokolov I, Simon C, Koopman J. Percolation on heterogeneous networks as a model for epidemics. Mathematical Biosciences. 2002;180:293. doi: 10.1016/S0025-5564(02)00117-7. - DOI - PubMed

Publication types