Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2020 Jan 28:10:1381.
doi: 10.3389/fgene.2019.01381. eCollection 2019.

Heterogeneous Multi-Layered Network Model for Omics Data Integration and Analysis

Bohyun Lee  1 , Shuo Zhang  1 , Aleksandar Poleksic  2 , Lei Xie  1   3   4   5
Affiliations
Review

Heterogeneous Multi-Layered Network Model for Omics Data Integration and Analysis

Bohyun Lee et al. Front Genet. .

Abstract

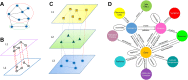
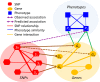
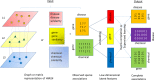
Advances in next-generation sequencing and high-throughput techniques have enabled the generation of vast amounts of diverse omics data. These big data provide an unprecedented opportunity in biology, but impose great challenges in data integration, data mining, and knowledge discovery due to the complexity, heterogeneity, dynamics, uncertainty, and high-dimensionality inherited in the omics data. Network has been widely used to represent relations between entities in biological system, such as protein-protein interaction, gene regulation, and brain connectivity (i.e. network construction) as well as to infer novel relations given a reconstructed network (aka link prediction). Particularly, heterogeneous multi-layered network (HMLN) has proven successful in integrating diverse biological data for the representation of the hierarchy of biological system. The HMLN provides unparalleled opportunities but imposes new computational challenges on establishing causal genotype-phenotype associations and understanding environmental impact on organisms. In this review, we focus on the recent advances in developing novel computational methods for the inference of novel biological relations from the HMLN. We first discuss the properties of biological HMLN. Then we survey four categories of state-of-the-art methods (matrix factorization, random walk, knowledge graph, and deep learning). Thirdly, we demonstrate their applications to omics data integration and analysis. Finally, we outline strategies for future directions in the development of new HMLN models.

Keywords: biological data analysis; biological network; data mining and knowledge discovery; deep learning; link prediction; machine learning; relation inference.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Illustration of three types of network models, (A) homogeneous network, where all nodes and edges are treated equally, even though they may belong to different types (dashed red and green circles). (B) multiplex network, (C) multi-layered network, (D) an example of heterogeneous multi-layered network HetioNet (Himmelstein and Baranzini, 2015).
Figure 2
Figure 2
An illustration of relation inference in the HMLN. The line thickness is proportional to the degree of relation. Arrowed and headed lines denote positive and negative relations, respectively.
Figure 3
Figure 3
An illustration of the common algorithmic framework for the relation inference (link prediction). HMLN is represented as a graph or collection of matrices. An inference algorithm takes the HMLN as input and generates a low-rank latent feature representation of chemicals, genes, and diseases, respectively. The inner product of latent features or supervised learning techniques will reconstruct complete gene-disease, chemical-disease, and chemical-gene association matrix.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Batmaz Z., Yurekli A., Bilge A., Kaleli C. (2019). A review on deep learning for recommender systems: challenges and remedies. Artif. Intell. Rev. 52, 1–37. 10.1007/s10462-018-9654-y - DOI
    1. Battaglia P. W., Hamrick J. B., Bapst V., Sanchez-Gonzalez A., Zambaldi V., Malinowski M., et al. (2018). Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261.
    1. Battiston F., Nicosia V., Latora V. (2014). Structural measures for multiplex networks. Phys. Rev. E 89, 032804. 10.1103/PhysRevE.89.032804 - DOI - PubMed
    1. Breese J. S., Heckerman D., Kadie C. (1998). “Empirical analysis of predictive algorithms for collaborative filtering” in Proceedings of the Fourteenth conference on Uncertainty in artificial intelligence (Morgan Kaufmann Publishers Inc.: Burlington, MA: ), 43–52.
    1. Cai L., Wang W. Y. (2017). Kbgan: Adversarial learning for knowledge graph embeddings. arXiv preprint arXiv:1711.04071.

LinkOut - more resources