Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Mar 19;65(6):065008.
doi: 10.1088/1361-6560/ab735f.

Locally optimized correlation-guided Bayesian adaptive regularization for ultrasound strain imaging

Rashid Al Mukaddim  1 , Nirvedh H Meshram, Tomy Varghese
Affiliations

Locally optimized correlation-guided Bayesian adaptive regularization for ultrasound strain imaging

Rashid Al Mukaddim et al. Phys Med Biol. .

Abstract

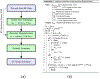
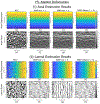
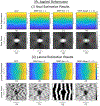
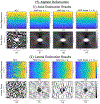
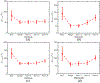
Ultrasound strain imaging utilizes radio-frequency (RF) ultrasound echo signals to estimate the relative elasticity of tissue under deformation. Due to the diagnostic value inherent in tissue elasticity, ultrasound strain imaging has found widespread clinical and preclinical applications. Accurate displacement estimation using pre and post-deformation RF signals is a crucial first step to derive high quality strain tensor images. Incorporating regularization into the displacement estimation framework is a commonly employed strategy to improve estimation accuracy and precision. In this work, we propose an adaptive variation of the iterative Bayesian regularization scheme utilizing RF similarity metric signal-to-noise ratio previously proposed by our group. The regularization scheme is incorporated into a 2D multi-level block matching (BM) algorithm for motion estimation. Adaptive nature of our algorithm is attributed to the dynamic variation of iteration number based on the normalized cross-correlation (NCC) function quality and a similarity measure between pre-deformation and motion compensated post-deformation RF signals. The proposed method is validated for either quasi-static and cardiac elastography or strain imaging applications using uniform and inclusion phantoms and canine cardiac deformation simulation models. Performance of adaptive Bayesian regularization was compared to conventional NCC and Bayesian regularization with fixed number of iterations. Results from uniform phantom simulation study show significant improvement in lateral displacement and strain estimation accuracy. For instance, at 1.5% lateral strain in a uniform phantom, Bayesian regularization with five iterations incurred a lateral strain error of 104.49%, which was significantly reduced using our adaptive approach to 27.51% (p < 0.001). Contrast-to-noise (CNR e ) ratios obtained from inclusion phantom indicate improved lesion detectability for both axial and lateral strain images. For instance, at 1.5% lateral strain, Bayesian regularization with five iterations had lateral CNR e of -0.31 dB which was significantly increased using the adaptive approach to 7.42 dB (p < 0.001). Similar results are seen with cardiac deformation modelling with improvement in myocardial strain images. In vivo feasibility was also demonstrated using data from a healthy murine heart. Overall, the proposed method makes Bayesian regularization robust for clinical and preclinical applications.

PubMed Disclaimer

Figures

Figure 1:
Figure 1:
(a) Flowchart describing AIBRF. (b) Proposed algorithm for adaptive refinement of NCC displacement estimates using Bayesian regularization.
Figure 2:
Figure 2:
Representative image of in vivo cardiac image acquisition experimental setup.
Figure 3:
Figure 3:
Representative axial (i) and lateral (ii) estimation results from uniform phantom simulation at 3 % applied deformation. Displacement images estimated by (a) NCC, (b) MAP-Iter=1, (c) MAP-Iter=5 and (d) MAP-Adapt along with corresponding strain images estimated by (e) NCC, (f) MAP-Iter=1, (g) MAP-Iter=5 and (h) MAP-Adapt respectively. l = maximum required iterations by MAP-Adapt.
Figure 4:
Figure 4:
Representative axial (i) and lateral (ii) estimation results from uniform phantom simulation at 7 % applied deformation. Displacement images estimated by (a) NCC, (b) MAP-Iter=1, (c) MAP-Iter=5 and (d) MAP-Adapt and corresponding strain images estimated by (e) NCC, (f) MAP-Iter=1, (g) MAP-Iter=5 and (h) MAP-Adapt respectively. l = maximum required iterations by MAP-Adapt.
Figure 5:
Figure 5:
Uniform phantom simulation error analysis as a function of the applied deformation. (a) Axial displacement MAE (μm), (b) axial displacement jitter error (μm2), (c) axial normalized strain error (%), (d) lateral displacement MAE (μm), (e) lateral displacement jitter error (μm2), (f) lateral normalized strain error (%) and (g) Maximum required number of iterations as a function of applied deformation for MAP-Adapt.
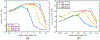
Figure 6:
Figure 6:
Comparison of experimental strain filters estimated using NCC, adaptive Bayesian and Bayesian with fixed iterations. (a) Axial strain filter and (b) lateral strain filter.
Figure 7:
Figure 7:
Representative axial (i) and lateral (ii) estimation results from inclusion phantom simulation at 3 % applied deformation. Displacement images estimated by (a) NCC, (b) MAP-Iter=1, (c) MAP-Iter=5 and (d) MAP-Adapt and corresponding strain images estimated by (e) NCC, (f) MAP-Iter=1, (g) MAP-Iter=5 and (h) MAP-Adapt respectively. l = maximum required iterations by MAP-Adapt.
Figure 8:
Figure 8:
Representative axial (i) and lateral (ii) estimation results from inclusion phantom simulation at 7 % applied deformation. Displacement images estimated by (a) NCC, (b) MAP-Iter=1, (c) MAP-Iter=5 and (d) MAP-Adapt along with corresponding strain images estimated by (e) NCC, (f) MAP-Iter=1, (g) MAP-Iter=5 and (h) MAP-Adapt respectively. l represents the maximum required iterations for the MAP-Adapt algorithm.
Figure 9:
Figure 9:
Inclusion phantom simulation error analysis as a function of the applied deformation. (a) Axial displacement MAE (μm), (b) axial displacement jitter error (μm2), (c) axial normalized strain error (%), (d) lateral displacement MAE (μm), (e) lateral displacement jitter error (μm2), and (f) lateral normalized strain error (%).
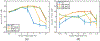
Figure 10:
Figure 10:
CNRe analysis of strain images estimated using NCC, adaptive Bayesian and Bayesian with fixed iterations. (a) Axial CNRe results and (b) Lateral CNRe results.
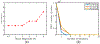
Figure 11:
Figure 11:
Adaptive variation of number of iterations against applied deformation. (a) Number of required iterations. (b) Number of pixels refined at each iteration.
Figure 12:
Figure 12:
Variation of (a) axial strain error (%), (b) lateral strain error (%) and (c) number of iterations as a function of improvement tolerance (ζ). Variation of (d) axial strain error (%), (e) lateral strain error (%) and (f) number of iterations as a function of decorrelation threshold (τ). Variation of (g) axial strain error (%), (h) lateral strain error (%) and (i) number of iterations as a function of iteration tolerance (TOL).
Figure 13:
Figure 13:
ES radial strain images for (a) FEA, (b) NCC, (c) MAP-Iter=3 and (d) MAP-Adapt respectively. ES longitudinal strain images for (e) FEA, (f) NCC, (g) MAP-Iter=3 and (h) MAP-Adapt respectively. l = required iterations by MAP-Adapt.
Figure 14:
Figure 14:
Performance evaluation of NCC, MAP-Adapt and MAP-Iter as a function of the number iterations. Figs. 14 (a) – (d) show axial strain error (%), lateral strain error (%), radial strain error (%) and longitudinal strain error (%) respectively.
Figure 15:
Figure 15:
(i) PLAX B-mode image at end-diastole with segmentation scheme. (ii) Radial strain estimation results. ES in vivo myocardial strain images with (a) NCC and (c) MAP-Adapt respectively. In vivo segmental strain curves with (b) NCC and (d) MAP-Adapt respectively. (iii) Longitudinal strain estimation results. ES in vivo myocardial strain images with (a) NCC and (c) MAP-Adapt respectively. In vivo segmental strain curves with (b) NCC and (d) MAP-Adapt respectively. l = median maximum required iterations by MAP-Adapt.
Figure 16:
Figure 16:
(i) PSAX B-mode image at end-diastole with segmentation scheme. (ii) Radial strain estimation results. ES in vivo myocardial strain images with (a) NCC and (c) MAP-Adapt respectively. In vivo segmental strain curves with (b) NCC and (d) MAP-Adapt respectively. (iii) Circumferential strain estimation results. ES in vivo myocardial strain images with (a) NCC and (c) MAP-Adapt respectively. In vivo segmental strain curves with (b) NCC and (d) MAP-Adapt respectively. l = median maximum required iterations by MAP-Adapt.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Al Mukaddim R, Meshram NH, Mitchell CC and Varghese T 2019. Hierarchical Motion Estimation With Bayesian Regularization in Cardiac Elastography: Simulation and $ In~Vivo $ Validation IEEE transactions on ultrasonics, ferroelectrics, and frequency control 66 1708–22 - PMC - PubMed
    1. Alam SK and Ophir J 1997. Reduction of signal decorrelation from mechanical compression of tissues by temporal stretching: Applications to elastography Ultrasound in Medicine and Biology 23 95–105 - PubMed
    1. Ashikuzzaman M, Gauthier CJ and Rivaz H 2019. Global Ultrasound Elastography in Spatial and Temporal Domains IEEE transactions on ultrasonics, ferroelectrics, and frequency control 66 876–87 - PubMed
    1. Bilgen M and Insana M 1997 IEEE Ultrasonics Symposium Proceedings. An International Symposium (Cat. No. 97CH36118), 1997), vol. Series 2): IEEE; ) pp 1427–30
    1. Bohs LN, Friemel BH, McDermott BA and Trahey GE 1993. A real time system for quantifying and displaying two-dimensional velocities using ultrasound Ultrasound in medicine & biology 19 751–61 - PubMed

Publication types