Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Feb 4;10(1):1758.
doi: 10.1038/s41598-020-58634-y.

Inferring quantity and qualities of superimposed reaction rates from single molecule survival time distributions

Matthias Reisser #  1 , Johannes Hettich #  1 , Timo Kuhn  1 , Achim P Popp  1 , Andreas Große-Berkenbusch  1 , J Christof M Gebhardt  2
Affiliations

Inferring quantity and qualities of superimposed reaction rates from single molecule survival time distributions

Matthias Reisser et al. Sci Rep. .

Abstract

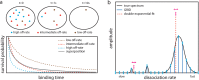
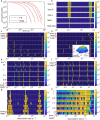
Actions of molecular species, for example binding of transcription factors to chromatin, may comprise several superimposed reaction pathways. The number and the rate constants of such superimposed reactions can in principle be resolved by inverse Laplace transformation of the corresponding distribution of reaction lifetimes. However, current approaches to solve this transformation are challenged by photobleaching-prone fluorescence measurements of lifetime distributions. Here, we present a genuine rate identification method (GRID), which infers the quantity, rates and amplitudes of dissociation processes from fluorescence lifetime distributions using a dense grid of possible decay rates. In contrast to common multi-exponential analysis of lifetime distributions, GRID is able to distinguish between broad and narrow clusters of decay rates. We validate GRID by simulations and apply it to CDX2-chromatin interactions measured by live cell single molecule fluorescence microscopy. GRID reveals well-separated narrow decay rate clusters of CDX2, in part overlooked by multi-exponential analysis. We discuss the amplitudes of the decay rate spectrum in terms of frequency of observed events and occupation probability of reaction states. We further demonstrate that a narrow decay rate cluster is compatible with a common model of TF sliding on DNA.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
Working principle of GRID. (a) Sketch of a TF exhibiting three distinct dissociation processes from chromatin (upper panel). The resulting survival time distribution is a superposition of the survival times of all three processes (lower panel). (b) Sketch of a decay rate spectrum (black solid line) underlying a complex survival time distribution. In common multi-exponential analysis, the number of decay rates has to be guessed and their values and amplitudes are varied (red dashed lines). In contrast, GRID only varies the amplitudes of a grid of decay rates (blue solid lines). Degrees of freedom are indicated by arrows.
Figure 2
Figure 2
Validation of GRID by simulations. (a) Simulated survival time distributions with dissociation rates of 0.1 s−1 and 5 s−1 and photobleaching rate of 1 s−1 (red lines) and distributions obtained using the results by GRID displayed in (b) (black dashed lines). (b) Comparison of different regularizations (specified in Methods) used in the cost function of GRID. The amplitudes of the spectra are colour coded. (c–h) Heat maps comparing the ground truth rate spectrum (indicated as Given) used to simulate survival time distributions (1st line) and the rate spectrum obtained by GRID (2nd line). Where applicable we added a 3rd line indicating the results of a multi-exponential approach. Simulations include a photobleaching rate of 1s−1, if not specified otherwise. Amplitudes are colour coded with logarithmic scale. The simulation parameters are summarized in Supplementary Table 1. (c) Behaviour of GRID for an increasing number of decay rates starting at k = 0.011 s−1 and separated by a factor of 4. (d) Behaviour of GRID for an increasing separation between two distinct decay rates with kfast = 5 s−1 and kslow varying in interval [0.01, 4] s−1. Inset: influence of the number of detected events and separation of decay rates on the accuracy of the inferred spectrum (Methods). (e) Effect of different photobleaching rate constants (indicated on the left) on inferring five irregularly spaced decay rates with different amplitudes. (f) Effect of varying amplitudes on inferring five irregularly spaced decay rates. (g) Increasing width of three decay rate clusters centred at kslow = 0.016 s−1, kint = 0.3 s−1 and kfast = 3.9 s−1. Relative width of clusters is up to 70%. (h) Behaviour of GRID in the case of survival probabilities following a power-law distribution for different values of the exponent (indicated on the left).
Figure 3
Figure 3
Dissociation rate spectrum of CDX2 – chromatin interactions. (a) Fluorescence survival time distributions of SiR-Halo-CDX2 obtained by live-cell single molecule tracking (grey symbols), fit with a tri-exponential model (blue lines) and distributions obtained using the results of GRID displayed in (b) (red lines). Time-lapse conditions are indicated above the distributions. The graph contains data from 10,653 molecules in 79 cells. Error bars denote s.d. (b) Event spectrum of CDX2 obtained by GRID using all data (red circles) and as an error estimate a heat map of 499 GRID results obtained by resampling 80% of data (blue colour code) (see Methods). (c) Sketch of the connection between single molecule tracking data and the corresponding event and state spectra. Upper panels: The event spectrum is obtained if molecules binding in a time interval are counted. This spectrum is a measure of an effective on-rate. To get from this kinetic rate constant to a state spectrum the binding time of these molecules has to be considered. Lower panels: The state spectrum is obtained, if molecules binding in a snapshot of time are counted. This spectrum depends on the on-rate as well as on the binding time of the molecules and is therefore a measure for the effective affinity (for details, see text and Methods). (d) State spectrum of CDX2 obtained by GRID using all data (red circles) and as an error estimate a heat map of 499 GRID results obtained by resampling 80% of data (blue colour code) (see Methods).
Figure 4
Figure 4
Model of TF sliding on chromatin and predicted standard deviation of dissociation rate clusters. (a) State diagram of a TF (red box) sliding on and dissociating from DNA. Each binding position is associated with an individual binding energy. The kinetic parameters are specified in Methods. (b) Standard deviation of dissociation rates as a function of sliding length. For each sliding length, dissociation rates were obtained from 500 simulations of the sliding model depicted in (a), where the sliding length of each segment has been kept constant but the base-pair content of each segment was varied for every simulation (for details see Methods).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Craig I, Thompson A, Thompson WJ. Practical numerical algorithms why laplace transforms are difficult to invert numerically. Computers in Physics. 1994;8:648–653.
    1. McWhirter J, Pike ER. On the numerical inversion of the Laplace transform and similar Fredholm integral equations of the first kind. Journal of Physics A: Mathematical and General. 1978;11:1729–1745. doi: 10.1088/0305-4470/11/9/007. - DOI
    1. Barone P, Ramponi A, Sebastiani G. On the numerical inversion of the Laplace transform for nuclear magnetic resonance relaxometry. Inverse Problems. 2001;17:77–94. doi: 10.1088/0266-5611/17/1/307. - DOI
    1. Berman P, Levi O, Parmet Y, Saunders M, Wiesman Z. Laplace inversion of low-resolution NMR relaxometry data using sparse representation methods. Concepts in Magnetic Resonance Part A. 2013;42:72–88. doi: 10.1002/cmr.a.21263. - DOI - PMC - PubMed
    1. Voelz VA, Pande VS. Calculation of rate spectra from noisy time series data. Proteins-Structure Function and Bioinformatics. 2012;80:342–351. doi: 10.1002/prot.23171. - DOI - PMC - PubMed

Publication types

LinkOut - more resources