Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 May 1;36(9):2862-2871.
doi: 10.1093/bioinformatics/btaa037.

Targeted realignment of LC-MS profiles by neighbor-wise compound-specific graphical time warping with misalignment detection

Chiung-Ting Wu  1 , Yizhi Wang  1 , Yinxue Wang  1 , Timothy Ebbels  2 , Ibrahim Karaman  3   4 , Gonçalo Graça  2 , Rui Pinto  3   4 , David M Herrington  5 , Yue Wang  1 , Guoqiang Yu  1
Affiliations

Targeted realignment of LC-MS profiles by neighbor-wise compound-specific graphical time warping with misalignment detection

Chiung-Ting Wu et al. Bioinformatics. .

Abstract

Motivation: Liquid chromatography-mass spectrometry (LC-MS) is a standard method for proteomics and metabolomics analysis of biological samples. Unfortunately, it suffers from various changes in the retention times (RT) of the same compound in different samples, and these must be subsequently corrected (aligned) during data processing. Classic alignment methods such as in the popular XCMS package often assume a single time-warping function for each sample. Thus, the potentially varying RT drift for compounds with different masses in a sample is neglected in these methods. Moreover, the systematic change in RT drift across run order is often not considered by alignment algorithms. Therefore, these methods cannot effectively correct all misalignments. For a large-scale experiment involving many samples, the existence of misalignment becomes inevitable and concerning.

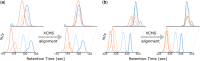
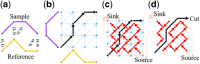
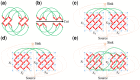
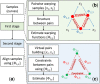
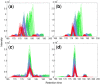
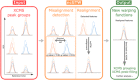
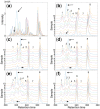
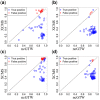
Results: Here, we describe an integrated reference-free profile alignment method, neighbor-wise compound-specific Graphical Time Warping (ncGTW), that can detect misaligned features and align profiles by leveraging expected RT drift structures and compound-specific warping functions. Specifically, ncGTW uses individualized warping functions for different compounds and assigns constraint edges on warping functions of neighboring samples. Validated with both realistic synthetic data and internal quality control samples, ncGTW applied to two large-scale metabolomics LC-MS datasets identifies many misaligned features and successfully realigns them. These features would otherwise be discarded or uncorrected using existing methods. The ncGTW software tool is developed currently as a plug-in to detect and realign misaligned features present in standard XCMS output.

Availability and implementation: An R package of ncGTW is freely available at Bioconductor and https://github.com/ChiungTingWu/ncGTW. A detailed user's manual and a vignette are provided within the package.

Supplementary information: Supplementary data are available at Bioinformatics online.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Examples of the observed misalignments due to single warping function assumption. Five samples over two m/z bins from each dataset are shown here for demonstration, where the upper and lower rows represent two different m/z bins, respectively (see details in Section 2.1). (a) An example from the Rotterdam dataset shows that even with similar RT, the drift of each sample could be significantly different in two m/z bins. Using only a single warping function, XCMS can only align one bin (the upper one) well but not the other one as shown in the right part. (b) A similar example is also observed in MESA dataset
Fig. 2.
Fig. 2.
Illustrative example on detecting misaligned features. After initial alignment, among the total 70 samples, relevant peaks are detected only in some samples (the indices in blue), and some of the feature(s) are obviously misaligned. With a lower resolution grouping by XCMS, these peaks are all grouped into one single feature, as shown between the two blue dashed lines. While with higher resolution grouping, this feature is split into three features 1–3 as separated by the red dashed lines. The sample index sets of these features are shown in red, respectively. The P-values of features 1–3 are all smaller than 0.05, thus pass the first criterion. Because the sample index sets of these three features are also disjoint, they pass the second criterion. Accordingly, ncGTW will detect the misalignment and realign the whole blue feature produced by the lower resolution grouping. (Color version of this figure is available at Bioinformatics online.)
Fig. 3.
Fig. 3.
Principle concept of DTW grid and graph. (a) DTW alignment aims to find the pairs of corresponding points over which the maximum profile similarity is achieved. Here the paired corresponding points are (1, 1), (2, 2), (3, 2), (4, 3) and (4, 4) that form the warping function. (b) DTW grid for solving the warping function shown in blue edges and dots, where the cost of each edge is determined by the intensity distance of each point pair. By solving the ‘shortest path’ problem, the warping function is obtained (black path) whose paired corresponding points are reflected in (a). (c) Based on the duality property of planar graph, DTW gird is transformed to DTW graph (red and orange lines and dots), where each red or orange edge crosses one blue edge, and the cost of red or orange edge is the same as the cost of blue edge. Note that orange lines link only the vertices (red dots enclosed by blue lined exterior triangle) to a single source or sink. Then, the shortest path problem becomes a maximum-flow/minimum-cut problem. (d) Solving the alignment problem is to find a ‘cut’ which separates the DTW graph into two parts with the minimum cost, with one part including the source and the other including the sink. The cut with the minimum cost corresponds to the warping function (black path). (Color version of this figure is available at Bioinformatics online.)
Fig. 4.
Fig. 4.
Construction of the various GTW graphs used in the different steps of ncGTW algorithm (Wang et al., 2016). (a) Two small DTW graphs are linked to form a GTW graph via additional ‘connecting’ edges (green lines between the vertices as the same position of two DTW graphs). (b) After adding the green edges, we can solve all warping functions at the same time, with the similarity among warping functions as constraints. The cost on green edges is to control the similarity between warping functions. For example, if the cost is very high, no green edge will be cut and all the warping functions would be the same. (c) GTW graph formed by two linked DTW graphs of two neighboring samples (x_i and x_(i+1)) with a common reference, extendable to all neighboring samples, where the orange lines link vertices to a single source or sink forming a large maximum flow graph, while green edges link the corresponding vertices of two DTW graphs (only edges linking top three vertices are shown here). (d) Part of the graph constructed in Stage 1 of ncGTW without using a common reference, where x_i and x_m are neighboring samples, and x_j and x_n are neighboring samples. (e) Part of the graph constructed in Stage 2 based on all pairwise warping functions obtained in Stage 1, where the warping function Φ_(i→j) guides the links between the corresponding vertices in GTW graphs, with x_c being the virtual reference. (Color version of this figure is available at Bioinformatics online.)
Fig. 5.
Fig. 5.
Flowchart of ncGTW algorithm. (a) With two-stage alignment strategy, all input samples (curves) are aligned simultaneously to a virtual reference. (b) Stage 1 of ncGTW with three illustrative samples. First, ncGTW builds a pairwise warping flow map (blue arrows). Then ncGTW incorporates structural information as the constraint and applies to all pairs (pair as red dot and constraint as a red dashed line). Lastly, ncGTW estimates all pairwise warping functions (Φ_(i,j)) jointly with e.g. smoothness constraint on neighboring sample pairs. (c) Stage 2 of ncGTW with three illustrative samples. ncGTW aligns every sample to a common virtual reference x_c, where the warping functions {Φ_(i,j)} obtained in Stage 1 provide warping correspondences and final warping functions {Φ_(i,c)} are calculated by solving the maximum flow problem. (Color version of this figure is available at Bioinformatics online.)
Fig. 6.
Fig. 6.
An illustrative experimental result on realignment and peak-distortion correction by ncGTW, where a feature from the MESA dataset was initially misaligned by XCMS. The color mapping (green to blue and blue to red) corresponds to the sample index. (a) Raw LC-MS data associated with the feature of interest (before alignment). (b) The misaligned feature by XCMS that has been correctly detected and reported by the misalignment detection module of ncGTW package. (c) Realignment by ncGTW where apices are well aligned but with observable peak shape distortion. (d) Peak shape distortion is efficiently corrected by the post-processing module of ncGTW package. (Color version of this figure is available at Bioinformatics online.)
Fig. 7.
Fig. 7.
Workflow of ncGTW. As a plug-in to XCMS, ncGTW uses the grouping results provided by XCMS as the inputs (one lower resolution and one higher resolution, as explained in Fig. 2). Then, ncGTW detects all misaligned features using the aforementioned criteria and performs realignment on these features. Lastly, ncGTW calculates final warping functions for each sample that can be sent back to XCMS for re-grouping or peak-filling
Fig. 8.
Fig. 8.
Illustrative realignment successfully performed by ncGTW incorporating ‘line’ structure in small-scale real LC-MS dataset. (a) LC-MS profiles of total ten samples. (b) The same LC-MS profiles but the curves are shifted to separate the curves. The 8 indexed peaks on sample 10 represent there are 8 peak groups. The peaks indicated by arrows in group 2 were misaligned by most peer methods except GTW and ncGTW. (c) The arrow-indicated peaks were wrongly aligned to the third peak group (and all peaks were severely distorted by DBA). (d) The arrow-indicated peaks were misaligned by CPM. (e) The arrow-indicated peaks were well-aligned by GTW while the fourth and fifth peak groups were misaligned. (f) All nine peak groups were correctly and accurately aligned by ncGTW in this challenging case
Fig. 9.
Fig. 9.
Application of ncGTW realignment method to Rotterdam and MESA datasets, where among the detected misaligned features, the blue circles represent true positives, and the red crosses represent false positives, respectively. (a) The average pairwise correlation coefficients on the Rotterdam dataset. (b) The average pairwise correlation coefficients on the MESA dataset. (c) The average pairwise total overlapping area on the Rotterdam dataset. (d) The average pairwise overlapping area on the MESA dataset. (Color version of this figure is available at Bioinformatics online.)
Fig. 10.
Fig. 10.
The comparisons of CV with versus without ncGTW realignment after the peak-filling step of XCMS. The blue circles represent the true positives and the red crosses represent the false positives. (a) The CV comparison on Rotterdam dataset. (b) The CV comparison on MESA dataset. (Color version of this figure is available at Bioinformatics online.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Arnold B.C. et al. (1992) A First Course in Order Statistics. Siam, Philadelphia, PA.
    1. Benk A.S., Roesli C. (2012) Label-free quantification using MALDI mass spectrometry: considerations and perspectives. Anal. Bioanal. Chem., 404, 1039–1056. - PubMed
    1. Bild D.E. et al. (2002) Multi-ethnic study of atherosclerosis: objectives and design. Am. J. Epidemiol., 156, 871–881. - PubMed
    1. Christin C. et al. (2008) Optimized time alignment algorithm for LC−MS data: correlation optimized warping using component detection algorithm-selected mass chromatograms. Anal. Chem., 80, 7012–7021. - PubMed
    1. Goldberg A.V. et al. (2011) Maximum flows by incremental breadth-first search In: European Symposium on Algorithms. Springer, Berlin, Heidelberg, pp. 457–468.

Publication types