Foundations of modeling in cryobiology-II: Heat and mass transport in bulk and at cell membrane and ice-liquid interfaces

doi:10.1016/j.cryobiol.2019.09.014

Review

. 2019 Dec:91:3-17.

doi: 10.1016/j.cryobiol.2019.09.014. Epub 2019 Oct 4.

Foundations of modeling in cryobiology-II: Heat and mass transport in bulk and at cell membrane and ice-liquid interfaces

Daniel M Anderson¹, James D Benson², Anthony J Kearsley³

Affiliations

¹ Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA; Department of Mathematical Sciences, George Mason University, Fairfax, VA, 22030, USA. Electronic address: danders1@gmu.edu.
² Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA; Department of Biology, University of Saskatchewan, Saskatoon, SK, S7N 5E2, Canada. Electronic address: james.benson@usask.ca.
³ Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA. Electronic address: anthony.kearsley@nist.gov.

PMID: 31589832
PMCID: PMC7098062
DOI: 10.1016/j.cryobiol.2019.09.014

Review

Foundations of modeling in cryobiology-II: Heat and mass transport in bulk and at cell membrane and ice-liquid interfaces

Daniel M Anderson et al. Cryobiology. 2019 Dec.

. 2019 Dec:91:3-17.

doi: 10.1016/j.cryobiol.2019.09.014. Epub 2019 Oct 4.

Authors

Daniel M Anderson¹, James D Benson², Anthony J Kearsley³

Affiliations

¹ Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA; Department of Mathematical Sciences, George Mason University, Fairfax, VA, 22030, USA. Electronic address: danders1@gmu.edu.
² Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA; Department of Biology, University of Saskatchewan, Saskatoon, SK, S7N 5E2, Canada. Electronic address: james.benson@usask.ca.
³ Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, MD, 20899-8910, USA. Electronic address: anthony.kearsley@nist.gov.

PMID: 31589832
PMCID: PMC7098062
DOI: 10.1016/j.cryobiol.2019.09.014

Abstract

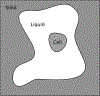
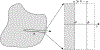
Modeling coupled heat and mass transport in biological systems is critical to the understanding of cryobiology. In Part I of this series we derived the transport equation and presented a general thermodynamic derivation of the critical components needed to use the transport equation in cryobiology. Here we refine to more cryobiologically relevant instances of a double free-boundary problem with multiple species. In particular, we present the derivation of appropriate mass and heat transport constitutive equations for a system consisting of a cell or tissue with a free external boundary, surrounded by liquid media with an encroaching free solidification front. This model consists of two parts-namely, transport in the "bulk phases" away from boundaries, and interfacial transport. Here we derive the bulk and interfacial mass, energy, and momentum balance equations and present a simplification of transport within membranes to jump conditions across them. We establish the governing equations for this cell/liquid/solid system whose solution in the case of a ternary mixture is explored in Part III of this series.

Keywords: Cryobiology; Interfacial conditions; Membrane boundary conditions; Transport processes.

PubMed Disclaimer

Figures

**Figure 1:**
Regions under consideration. Solid lines indicate interfaces. Bulk transport occurs away from solid lines. Here we make no assumptions about region geometry.

**Figure 2:**
Schematic of a typical pillbox balance equation. We assume the total width dx⁺ + dx⁻ and cross sectional area A are constant from time t to t + dt. We have that $d x^{-} = d x_{o}^{-} + V_{n}$ and $d x^{+} = d x_{o}^{+} - V_{n} d t$ . The volume in the left region at time t, for example, is given by $A d x_{o}^{-}$ , and if, for example, [ρ] =mass/volume, then the mass at time t is $ρ^{-} A d x_{o}^{-} + ρ^{+} A d x_{o}^{+} = (ρ^{-} d x_{o}^{-} + ρ^{+} d x_{o}^{+}) A$ and the mass at time t + dt is $(ρ^{-} d x^{-} + ρ^{+} d x^{+}) A = ρ^{-} (d x_{o}^{-} + V_{n} d t) A + ρ^{+} (d x_{o}^{+} - V_{n} d t) A$ . The change of mass from t to t + dt is then (ρ⁻ − ρ⁺)V_nAdt. On the other hand, note that if the velocity into the left region is v⁻ and the velocity out of the right region is v⁺, then the normal velocity is $v \cdot \hat{n}$ and the mass flux over time dt is $(ρ^{-} v^{-} - ρ^{+} v^{+}) \cdot \hat{n} A d t$ .

**Figure 3:**
Schematic of cell membrane. The interior radius is a and the exterior is b and we assume a ≫ b – a.

See this image and copyright information in PMC

Cited by

Simple Syntheses of New Pegylated Trehalose Derivatives as a Chemical Tool for Potential Evaluation of Cryoprotectant Effects on Cell Membrane.
Pomeisl K, Richter J, Golan M, Kratochvílová I. Pomeisl K, et al. Molecules. 2020 Jan 23;25(3):497. doi: 10.3390/molecules25030497. Molecules. 2020. PMID: 31979348 Free PMC article.
Loading equine oocytes with cryoprotective agents captured with a finite element method model.
Içli S, Soleimani M, Oldenhof H, Sieme H, Wriggers P, Wolkers WF. Içli S, et al. Sci Rep. 2021 Oct 6;11(1):19812. doi: 10.1038/s41598-021-99287-9. Sci Rep. 2021. PMID: 34615933 Free PMC article.
Foundations of modeling in cryobiology-III: Inward solidification of a ternary solution towards a permeable spherical cell in the dilute limit.
Anderson DM, Benson JD, Kearsley AJ. Anderson DM, et al. Cryobiology. 2020 Feb 1;92:34-46. doi: 10.1016/j.cryobiol.2019.09.013. Epub 2019 Oct 8. Cryobiology. 2020. PMID: 31604066 Free PMC article.

References

1. Abazari A, Elliott JAW, Law GK, McGann LE, and Jomha NM. A biomechanics triphasic approach to the transport of non dilute solutions in articular cartilage. Biophys. Journal, 97:3054–3064, 2009. - PMC - PubMed
1. Abazari A, Thompson RB, Elliott JAW, and McGann LE. Transport phenomena in articular cartilage cryopreservation as predicted by the modified triphasic model and the effect of natural inhomogeneities. Biophysical Journal, 102(6):1284–1293, 2012. - PMC - PubMed
1. Acker JP, Elliott JAW, and McGann LE. Intercellular ice propagation: experimental evidence for ice growth through membrane pores. Biophys J, 81(3):1389–97, September 2001. - PMC - PubMed
1. Aitta A, Huppert HE, and Worster MG. Diffusion-controlled solidification of a ternary melt from a cooled boundary. J. Fluid Mech, 432: 201–217, 2001.
1. Ambrosi D and Preziosi L. Modeling injection molding processes with deformable porous preforms. SIAM J. Appl. Math, 61:22–42, 2000.

Publication types

Actions
Actions
Actions
Actions

MeSH terms

Actions
Actions
Actions
Actions
Actions
Actions
Actions

Substances

Actions

Grants and funding

R01 HD083930/HD/NICHD NIH HHS/United States

LinkOut - more resources

Full Text Sources

[1] Abazari A, Elliott JAW, Law GK, McGann LE, and Jomha NM. A biomechanics triphasic approach to the transport of non dilute solutions in articular cartilage. Biophys. Journal, 97:3054–3064, 2009. - PMC - PubMed

[2] Abazari A, Elliott JAW, Law GK, McGann LE, and Jomha NM. A biomechanics triphasic approach to the transport of non dilute solutions in articular cartilage. Biophys. Journal, 97:3054–3064, 2009. - PMC - PubMed

[3] Abazari A, Thompson RB, Elliott JAW, and McGann LE. Transport phenomena in articular cartilage cryopreservation as predicted by the modified triphasic model and the effect of natural inhomogeneities. Biophysical Journal, 102(6):1284–1293, 2012. - PMC - PubMed

[4] Abazari A, Thompson RB, Elliott JAW, and McGann LE. Transport phenomena in articular cartilage cryopreservation as predicted by the modified triphasic model and the effect of natural inhomogeneities. Biophysical Journal, 102(6):1284–1293, 2012. - PMC - PubMed

[5] Acker JP, Elliott JAW, and McGann LE. Intercellular ice propagation: experimental evidence for ice growth through membrane pores. Biophys J, 81(3):1389–97, September 2001. - PMC - PubMed

[6] Acker JP, Elliott JAW, and McGann LE. Intercellular ice propagation: experimental evidence for ice growth through membrane pores. Biophys J, 81(3):1389–97, September 2001. - PMC - PubMed

[7] Aitta A, Huppert HE, and Worster MG. Diffusion-controlled solidification of a ternary melt from a cooled boundary. J. Fluid Mech, 432: 201–217, 2001.

[8] Aitta A, Huppert HE, and Worster MG. Diffusion-controlled solidification of a ternary melt from a cooled boundary. J. Fluid Mech, 432: 201–217, 2001.

[9] Ambrosi D and Preziosi L. Modeling injection molding processes with deformable porous preforms. SIAM J. Appl. Math, 61:22–42, 2000.

[10] Ambrosi D and Preziosi L. Modeling injection molding processes with deformable porous preforms. SIAM J. Appl. Math, 61:22–42, 2000.

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Foundations of modeling in cryobiology-II: Heat and mass transport in bulk and at cell membrane and ice-liquid interfaces

Affiliations

Foundations of modeling in cryobiology-II: Heat and mass transport in bulk and at cell membrane and ice-liquid interfaces

Authors

Affiliations

Abstract

Figures

Similar articles

Cited by

References

Publication types

MeSH terms

Substances

Grants and funding

LinkOut - more resources

Full Text Sources