Polymer Modeling Predicts Chromosome Reorganization in Senescence

doi:10.1016/j.celrep.2019.08.045

. 2019 Sep 17;28(12):3212-3223.e6.

doi: 10.1016/j.celrep.2019.08.045.

Polymer Modeling Predicts Chromosome Reorganization in Senescence

Michael Chiang¹, Davide Michieletto², Chris A Brackley³, Nattaphong Rattanavirotkul⁴, Hisham Mohammed⁵, Davide Marenduzzo³, Tamir Chandra⁶

Affiliations

¹ SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK. Electronic address: c.h.m.chiang@sms.ed.ac.uk.
² SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK; MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK; Centre for Mathematical Biology, and Department of Mathematical Sciences, University of Bath, North Road, Bath BA2 7AY, UK.
³ SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK.
⁴ MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK.
⁵ Cancer Early Detection Advanced Research Center, Knight Cancer Institute, Department of Molecular and Medical Genetics, Oregon Health & Science University, Portland, OR 97239, USA.
⁶ MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK. Electronic address: tamir.chandra@igmm.ed.ac.uk.

PMID: 31533042
PMCID: PMC6859504
DOI: 10.1016/j.celrep.2019.08.045

Polymer Modeling Predicts Chromosome Reorganization in Senescence

Michael Chiang et al. Cell Rep. 2019.

. 2019 Sep 17;28(12):3212-3223.e6.

doi: 10.1016/j.celrep.2019.08.045.

Authors

Michael Chiang¹, Davide Michieletto², Chris A Brackley³, Nattaphong Rattanavirotkul⁴, Hisham Mohammed⁵, Davide Marenduzzo³, Tamir Chandra⁶

Affiliations

¹ SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK. Electronic address: c.h.m.chiang@sms.ed.ac.uk.
² SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK; MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK; Centre for Mathematical Biology, and Department of Mathematical Sciences, University of Bath, North Road, Bath BA2 7AY, UK.
³ SUPA, School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK.
⁴ MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK.
⁵ Cancer Early Detection Advanced Research Center, Knight Cancer Institute, Department of Molecular and Medical Genetics, Oregon Health & Science University, Portland, OR 97239, USA.
⁶ MRC Human Genetics Unit, MRC Institute of Genetics and Molecular Medicine, University of Edinburgh, Western General Hospital, Crewe Road South, Edinburgh EH4 2XU, UK. Electronic address: tamir.chandra@igmm.ed.ac.uk.

PMID: 31533042
PMCID: PMC6859504
DOI: 10.1016/j.celrep.2019.08.045

Abstract

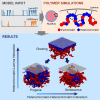
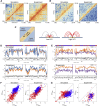
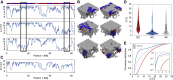
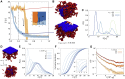
Lamina-associated domains (LADs) cover a large part of the human genome and are thought to play a major role in shaping the nuclear architectural landscape. Here, we perform polymer simulations, microscopy, and mass spectrometry to dissect the roles played by heterochromatin- and lamina-mediated interactions in nuclear organization. Our model explains the conventional organization of heterochromatin and euchromatin in growing cells and the pathological organization found in oncogene-induced senescence and progeria. We show that the experimentally observed changes in the locality of contacts in senescent and progeroid cells can be explained as arising due to phase transitions in the system. Within our simulations, LADs are highly stochastic, as in experiments. Our model suggests that, once established, the senescent phenotype should be metastable even if lamina-mediated interactions were reinstated. Overall, our simulations uncover a generic physical mechanism that can regulate heterochromatin segregation and LAD formation in a wide range of mammalian nuclei.

Keywords: cellular senescence; genome organization; heterochromatin; nuclear lamina; phase transitions; polymer simulations; progeria.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

**Figure 1**
A Polymer Model for Lamina-Mediated Chromosome Organization in Different Cell States (A) A subsection of the nuclear periphery and human chromosome 20 were simulated. Chromatin was modeled as a flexible bead-spring chain, with red beads representing euchromatin (EC) and blue beads representing heterochromatin (HC). The nuclear lamina (NL) was represented as a layer of static beads (gray). Chromatin beads were labeled HC if the corresponding genomic region was enriched in H3K9me3 and/or LaminB1. Beads corresponding to the centromeric region (26.4–29.4 Mb) were also treated as HC. All of the other beads were labeled EC. EC and HC beads can interact with beads of the same kind with interaction strength $ϵ_{EE}$ and $ϵ_{HH}$ , respectively. HC beads can also interact with the NL beads with interaction strength $ϵ_{HL}$ . (B) A simulation snapshot of the model when the HC-HC and HC-NL interactions are weak.

**Figure 2**
Variations of the Two Model Parameters Reproduce Chromatin Organization in Growing, Senescent, and Progeroid Cells (A) A heatmap showing the distance $\bar{z}$ between the center of mass of the chromosome from the NL across the parameter space $(ϵ_{HH}, ϵ_{HL})$ . Ten simulations were performed for every 0.2 increment in both $ϵ_{HH}$ and $ϵ_{HL}$ directions. Distances are reported in units of the bead size ( $σ \approx 70$ nm). The pink line separating the adsorbed and desorbed regime was estimated based on the inflection points in $\bar{z}$ when varying $ϵ_{HL}$ for fixed $ϵ_{HH}$ . $\bar{z}$ also captures the transition between the collapsed and extended phase in the adsorbed regime, as a compact fiber would stay closer to the NL. The cyan line reports the inflection points at which this transition occurs. (B) A heatmap showing the average local number density $ρ$ of chromatin beads across the parameter space. The cyan line separating the extended and collapsed phases was estimated based on the inflection points in $ρ$ . Its location is consistent with that estimated from $\bar{z}$ . The interaction strengths for extended and collapsed conformation are also in line with recent studies on chromatin structure in yeast (Socol et al., 2019) and *Drosophila* (Lesage et al., 2019). (C) A full-phase diagram of the four observed phases: adsorbed-extended (AE), adsorbed-collapsed (AC), desorbed-extended (DE), and desorbed-collapsed (DC). The boundary lines are those from (A) and (B). (D) Simulation snapshots of the four phases. (E) Illustrations of chromatin structures for cells in growing, senescent, and progeroid conditions. (F) Cross-sectional view of a simulation snapshot corresponding to the DC or senescent phase. (G) Time-averaged density profiles of HC and EC as a function of distance r from the center of the globule. (H) Confocal images of chromosomes in senescent cells with DAPI, H3K27me3, and H3K9me3 staining. Scale bars indicate 10 μm. (I) Enlarged view of an SAHF corresponding to the white square in the combined image in (H). (J) Corresponding intensity profiles for H3K9me3 and H3K27me3 along the white line in (I).

**Figure 3**
Chromatin Contact Network and the Open Chromatin Index (OCI) in Growing (AC), Senescent (DC), and Progeroid (DE) Phases (A and B) Heatmaps comparing the contact frequencies between (A) growing and senescence and (B) growing and progeria in simulations and experiments. In our simulations, we used $(ϵ_{HH}, ϵ_{HL}) = (1.0, 1.6)$ for growing, $(1.4, 0.2)$ for senescence, and $(0.2, 0.2)$ for progeria. We performed 20 simulations for each case. We used Hi-C data from Chandra et al. (2015) for the comparison between growing and senescence, and data from McCord et al. (2013) for the comparison between growing and progeria. The contact frequencies are plotted in log scale to aid visualization. (C) The open chromatin index (OCI). Contacts were defined to be local or distal based on a threshold $s_{d}$ , which was set to 2 Mb (close to the maximum size of a TAD [Dekker and Heard, 2015]; see STAR Methods). (D and E) The OCI value of each bin in the heatmap for (D) growing and senescence and (E) growing and progeria. Their difference (ΔOCI) is shown in the bottom track. The top track indicates the chromatin state along the polymer (i.e., red for EC, blue for HC, and gray for centromeric region). (F and G) Scatterplots of the OCI value of each bin for (F) growing versus senescence and (G) growing versus progeria. The color of each point indicates the chromatin state of the corresponding bin (treating centromeric region as HC).

**Figure 4**
Simulations Show Stochasticity in Chromatin Contacts with the NL (A) Plots showing the distance $z_{c}$ of each chromatin bead from the horizontal plane at the center of the simulation box for three simulation runs in the growing (AC) phase $(ϵ_{HH} = 1.0, ϵ_{HL} = 1.6)$ . As the NL is located at the top of the box $(z_{c} \approx 17 σ)$ , a high value in $z_{c}$ indicates that the bead is close to the NL. The x axis shows the genomic position corresponding to each bead. The top track indicates the chromatin state along the polymer. (B) Snapshots of the simulation runs coloring only the beads within the two highlighted regions in (A) (rectangular boxes). These figures reveal that the same chromatin segment can reside in different positions relative to the NL in different runs, which is consistent with experimental observations that LADs associate with the NL stochastically. (C) The average value of $z_{c}$ for each bead over 20 simulations. (D) Violin plots showing the distributions of the distance z from the NL for EC, HC, and all beads. (E) Cumulative distributions of z for EC, HC, and all beads. The inset shows the distributions (in log-linear form) for small z.

**Figure 5**
The Transition between the Growing (AC) and Senescent (DC) Phase Is Abrupt and History Dependent (A) The distance $\bar{z}$ between the center of mass of the chromosome and the NL, averaged over five simulation runs in which we fix $ϵ_{HH} = 1.0$ and gradually decrease $ϵ_{HL}$ from 1.2 to 0.2 over $10^{6}$ Brownian time steps, before increasing it back to 1.2 over the same time (its path in the phase diagram is shown in the inset). The shaded area around the curve reports the SD of the mean. The dashed line marks the predicted transition point between the adsorbed and desorbed regime at $ϵ_{HH} = 1.0$ (see Figures 2A and 2C). Hysteresis occurs in the region $ϵ_{HL} \sim 0.3$ –0.6. (B) Snapshots of the system at $ϵ_{HL} = 0.5$ showing that it can either be in the AC (growing) or the DC (senescent) phase, depending on its history. (C) The probability density function of $\bar{z}$ at $ϵ_{HL} = 0.3$ , 0.4, and 0.5 ( $ϵ_{HH} = 1.0$ ; 50 simulations were sampled for each parameter set). A bimodal behavior is found when $ϵ_{HL} \sim 0.4$ , suggesting the coexistence of both the AC and DC phases. (D) Snapshots of our simulation modeling the process of LADs detachment from the NL, during which we change $ϵ_{HL}$ instantaneously from 1.2 to 0.2. (E) The probability density function of the distance z of each bead from the NL at time t after $ϵ_{HL}$ has been reduced (sampled from ten simulations). (F) The corresponding cumulative distribution of z. The inset shows the distribution for small z in log-linear form. (G) A log-linear plot of the fraction of beads ψ in contact with the NL (those whose distance from the NL is less than δ) at time t after the weakening in $ϵ_{HL}$ , for three different thresholds of δ. The black curves are stretch exponential fits $f (t) = κ \exp (- α t^{β})$ . The fitted stretch exponents β are 0.56, 0.58, and 0.61 for $δ = 2$ , 3, and $4 σ$ , respectively.

See this image and copyright information in PMC

Cited by

A Lamin-Associated Chromatin Model for Chromosome Organization.
Maji A, Ahmed JA, Roy S, Chakrabarti B, Mitra MK. Maji A, et al. Biophys J. 2020 Jun 16;118(12):3041-3050. doi: 10.1016/j.bpj.2020.05.014. Epub 2020 May 20. Biophys J. 2020. PMID: 32492372 Free PMC article.
Mechanistic modeling of chromatin folding to understand function.
Brackey CA, Marenduzzo D, Gilbert N. Brackey CA, et al. Nat Methods. 2020 Aug;17(8):767-775. doi: 10.1038/s41592-020-0852-6. Epub 2020 Jun 8. Nat Methods. 2020. PMID: 32514111 Review.
Mesoscale, long-time mixing of chromosomes and its connection to polymer dynamics.
Bajpai G, Safran S. Bajpai G, et al. PLoS Comput Biol. 2023 May 25;19(5):e1011142. doi: 10.1371/journal.pcbi.1011142. eCollection 2023 May. PLoS Comput Biol. 2023. PMID: 37228178 Free PMC article.
Phase Separation and Correlated Motions in Motorized Genome.
Jiang Z, Qi Y, Kamat K, Zhang B. Jiang Z, et al. J Phys Chem B. 2022 Aug 4;126(30):5619-5628. doi: 10.1021/acs.jpcb.2c03238. Epub 2022 Jul 20. J Phys Chem B. 2022. PMID: 35858189 Free PMC article.
Biology and Model Predictions of the Dynamics and Heterogeneity of Chromatin-Nuclear Lamina Interactions.
Madsen-Østerbye J, Bellanger A, Galigniana NM, Collas P. Madsen-Østerbye J, et al. Front Cell Dev Biol. 2022 May 26;10:913458. doi: 10.3389/fcell.2022.913458. eCollection 2022. Front Cell Dev Biol. 2022. PMID: 35693945 Free PMC article. Review.

See all "Cited by" articles

References

1. Barbieri M., Chotalia M., Fraser J., Lavitas L.M., Dostie J., Pombo A., Nicodemi M. Complexity of chromatin folding is captured by the strings and binders switch model. Proc. Natl. Acad. Sci. USA. 2012;109:16173–16178. - PMC - PubMed
1. Barbieri M., Fraser J., Lavitas L.M., Chotalia M., Dostie J., Pombo A., Nicodemi M. A polymer model explains the complexity of large-scale chromatin folding. Nucleus. 2013;4:267–273. - PMC - PubMed
1. Binder K. Theory of first-order phase transitions. Rep. Prog. Phys. 1987;50:783–859.
1. Bonev B., Cavalli G. Organization and function of the 3D genome. Nat. Rev. Genet. 2016;17:661–678. - PubMed
1. Boumendil C., Hari P., Olsen K.C.F., Acosta J.C., Bickmore W.A. Nuclear pore density controls heterochromatin reorganization during senescence. Genes Dev. 2019;33:144–149. - PMC - PubMed

MeSH terms

Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions

Substances

Actions
Actions

LinkOut - more resources

Full Text Sources
Research Materials
- Addgene Non-profit plasmid repository
Miscellaneous
- SciCrunch

[1] Barbieri M., Chotalia M., Fraser J., Lavitas L.M., Dostie J., Pombo A., Nicodemi M. Complexity of chromatin folding is captured by the strings and binders switch model. Proc. Natl. Acad. Sci. USA. 2012;109:16173–16178. - PMC - PubMed

[2] Barbieri M., Chotalia M., Fraser J., Lavitas L.M., Dostie J., Pombo A., Nicodemi M. Complexity of chromatin folding is captured by the strings and binders switch model. Proc. Natl. Acad. Sci. USA. 2012;109:16173–16178. - PMC - PubMed

[3] Barbieri M., Fraser J., Lavitas L.M., Chotalia M., Dostie J., Pombo A., Nicodemi M. A polymer model explains the complexity of large-scale chromatin folding. Nucleus. 2013;4:267–273. - PMC - PubMed

[4] Barbieri M., Fraser J., Lavitas L.M., Chotalia M., Dostie J., Pombo A., Nicodemi M. A polymer model explains the complexity of large-scale chromatin folding. Nucleus. 2013;4:267–273. - PMC - PubMed

[5] Binder K. Theory of first-order phase transitions. Rep. Prog. Phys. 1987;50:783–859.

[6] Binder K. Theory of first-order phase transitions. Rep. Prog. Phys. 1987;50:783–859.

[7] Bonev B., Cavalli G. Organization and function of the 3D genome. Nat. Rev. Genet. 2016;17:661–678. - PubMed

[8] Bonev B., Cavalli G. Organization and function of the 3D genome. Nat. Rev. Genet. 2016;17:661–678. - PubMed

[9] Boumendil C., Hari P., Olsen K.C.F., Acosta J.C., Bickmore W.A. Nuclear pore density controls heterochromatin reorganization during senescence. Genes Dev. 2019;33:144–149. - PMC - PubMed

[10] Boumendil C., Hari P., Olsen K.C.F., Acosta J.C., Bickmore W.A. Nuclear pore density controls heterochromatin reorganization during senescence. Genes Dev. 2019;33:144–149. - PMC - PubMed

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Polymer Modeling Predicts Chromosome Reorganization in Senescence

Affiliations

Polymer Modeling Predicts Chromosome Reorganization in Senescence

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

Similar articles

Cited by

References

MeSH terms

Substances

LinkOut - more resources

Full Text Sources

Research Materials

Miscellaneous

Abstract

Conflict of interest statement

Figures

Similar articles

Cited by

References

MeSH terms

Substances

Related information

LinkOut - more resources

Full Text Sources

Research Materials

Miscellaneous