Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Dec 4;9(1):5166.
doi: 10.1038/s41467-018-07437-x.

High-performance reconstruction of microscopic force fields from Brownian trajectories

Laura Pérez García  1 , Jaime Donlucas Pérez  1 , Giorgio Volpe  2 , Alejandro V Arzola  3 , Giovanni Volpe  4
Affiliations

High-performance reconstruction of microscopic force fields from Brownian trajectories

Laura Pérez García et al. Nat Commun. .

Abstract

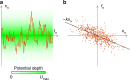
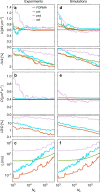
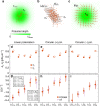
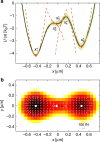
The accurate measurement of microscopic force fields is crucial in many branches of science and technology, from biophotonics and mechanobiology to microscopy and optomechanics. These forces are often probed by analysing their influence on the motion of Brownian particles. Here we introduce a powerful algorithm for microscopic force reconstruction via maximum-likelihood-estimator analysis (FORMA) to retrieve the force field acting on a Brownian particle from the analysis of its displacements. FORMA estimates accurately the conservative and non-conservative components of the force field with important advantages over established techniques, being parameter-free, requiring ten-fold less data and executing orders-of-magnitude faster. We demonstrate FORMA performance using optical tweezers, showing how, outperforming other available techniques, it can identify and characterise stable and unstable equilibrium points in generic force fields. Thanks to its high performance, FORMA can accelerate the development of microscopic and nanoscopic force transducers for physics, biology and engineering.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Fig. 1
Fig. 1
Force reconstruction via maximum-likelihood-estimator analysis. Schematic of the 1D version of FORMA for a particle held in an optical tweezers. a While a particle is held within a harmonic optical trap generated by an optical tweezers (the green background illustrates the depth of the potential), samples xn of its trajectory (solid orange line) are acquired at times tn. b FORMA exploits the fact that the stiffness k of the optical tweezers is related to the correlation between xn and the friction force fn acting on the particle (each dot represents a different (xn, fn) pair). FORMA uses an MLE to quickly, precisely, and accurately estimate this correlation and, thus, k. The spread of the dots around the linear regression line −kxn provides information about the diffusion coefficient D of the particle
Fig. 2
Fig. 2
Better performance of FORMA compared to alternative techniques. Experimentally determined values of a the trap stiffness k and its relative error δk/k, b the diffusion coefficient D and its relative error δD/D, and c the computational execution time tc as a function of the sample number Ns for FORMA (orange lines); and d–f corresponding results from numerical simulations. The comparisons with potential (green lines), PSD (blue lines), and ACF (pink lines) analyses show that FORMA converges faster (i.e. for smaller Ns), is more precise (i.e. smaller relative errors), is more accurate (i.e. it converges to the expected value represented by the black dashed line), and executes faster than the other methods. In all cases, we have acquired/simulated 24 trajectories of the motion of a spherical microparticle with radius R = 0.48 μm in an aqueous medium of viscosity η = 0.0011 Pa s−1 at a sampling frequency fs = 4504.5 s−1. The relative errors are obtained as the standard deviations of the estimations over the 24 trajectories. The execution times are measured using a MatLab implementation of the algorithms on a laptop computer (processor Intel Core i7 at 2.2 GHz and 8 GB 1600 MHz DDR3)
Fig. 3
Fig. 3
Measurement of the non-conservative force-field component. a–c Schematic of the 2D version of FORMA for a particle held in an optical tweezers: a Samples rn of a particle trajectory (solid orange line) held in an optical tweezers (the green background illustrates the depth of the potential) are acquired at times tn. b FORMA estimates the Jacobian J0 of the force field from the relation between rn and fn using a 2D MLE. In the schematic, we represent only the estimation of the first row of J0, which is related to the x-component of fn; the complete graph cannot be represented because it is 4D. c Using this information, FORMA reconstructs the force field around the equilibrium point req (see also Supplementary Figure 3). d–f Stiffnesses kx and ky, and g–i angular frequency Ω of a Brownian particle optically trapped by d, g a linearly polarised, e, h circularly (+) polarised, and f, i circularly (−) polarised Laguerre-Gaussian (LG) beam with l = −2, −1, 0, 1,2. g–i The results of FORMA (orange circles) agree well with the results of the CCF analysis (pink triangles). The insets in g show the force fields for the case of a Gaussian beam (LG0), which is purely conservative (l = 0), and of a beam with a charge l = 2 of orbital angular moment (LG2), which features a non-conservative component that only induces a mild bending of the arrows. In all cases, we have acquired trajectories of the motion of a spherical particle with radius R = 0.48 μm in an aqueous medium of viscosity η = 0.0011 Pa s−1 at a sampling frequency fs = 4504.5 s−1, and used 25 windows of 105 samples for the analysis; the error bars in d–i are the standard deviations over these 25 measurements
Fig. 4
Fig. 4
Reconstruction of stable and unstable equilibrium points. a Multiwell optical potential generated by two focused Gaussian beams slightly displaced along the x-direction. FORMA identifies three stable (x1*, x3*, x5*; full circles) and two unstable (x2*, x4*; empty circles) equilibrium points, and measures their stiffness (orange solid and dashed lines). The corresponding x-potential obtained from the potential method is shown by the green solid line (the green shaded area represents one standard deviation obtained repeating the experiment 20 times). b 2D plot of the force field measured with FORMA (arrows) and of the potential measured with the potential analysis (background colour). The stable and unstable equilibrium points are indicated by the full and empty circles, respectively. We have acquired trajectories of the motion of a spherical particle with radius R = 0.48 μm in an aqueous medium of viscosity η = 0.0011 Pa s−1 at a sampling frequency fs = 4504.5 s−1, and used 20 windows of 4.5 × 105 samples for the analysis
Fig. 5
Fig. 5
Reconstruction of the equilibrium points in a speckle pattern. a The intensity of the speckle (green background, laser wavelength λ = 532 nm) is approximately proportional to the potential depth of the optical potential felt by a particle whose size (particle diameter 1.00 ± 0.04 μm) is similar to the speckle characteristic size (2.8 μm), . FORMA identifies several stable (full circles) and unstable (empty circles) equilibrium points, and measures the orientation of the principal axes (θ), the stiffnesses along them (k1 and k2), and angular frequency (Ω) (see Supplementary Table 2 for the measured values). We have acquired trajectories of the motion of a spherical particle with radius R = 0.50 ± 0.02 μm in an aqueous medium of viscosity η = 0.0013 Pa s−1 at a sampling frequency fs = 600 s−1; as we cannot expect the particle to spontaneously diffuse over the whole speckle field during the time of the experiment, we have placed this particle in 25 positions within the speckle field and let it diffuse each time acquiring 2 × 106 samples for the analysis. b–d Examples of reconstructed force fields around b a stable point, c an unstable point with a significant rotational component (indicated by the arrow), and d two stable points with a saddle in between; the grey arrows plot the 2D force field measured with FORMA and are scaled by a different factor in each plot
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev. Mod. Phys. 2014;86:1391–1452. doi: 10.1103/RevModPhys.86.1391. - DOI
    1. Moerner WE. Single-molecule spectroscopy, imaging, and photocontrol: foundations for super-resolution microscopy (Nobel lecture) Ang. Chem. Int. Ed. 2015;54:8067–8093. doi: 10.1002/anie.201501949. - DOI - PubMed
    1. Roca-Cusachs P, Conte V, Trepat X. Quantifying forces in cell biology. Nat. Cell Biol. 2017;19:742–751. doi: 10.1038/ncb3564. - DOI - PubMed
    1. Jones PH, Maragò OM, Volpe G. Optical tweezers: Principles and applications. Cambridge: Cambridge University Press; 2015.
    1. Florin EL, Pralle A, Stelzer EHK, Hörber JKH. Photonic force microscope calibration by thermal noise analysis. Appl. Phys. A. 1998;66:S75–S78. doi: 10.1007/s003390051103. - DOI

Publication types