Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Oct 1;14(10):e1006505.
doi: 10.1371/journal.pcbi.1006505. eCollection 2018 Oct.

Exploring the impact of inoculum dose on host immunity and morbidity to inform model-based vaccine design

Andreas Handel  1 , Yan Li  2 , Brian McKay  3 , Kasia A Pawelek  4 , Veronika Zarnitsyna  5 , Rustom Antia  6
Affiliations

Exploring the impact of inoculum dose on host immunity and morbidity to inform model-based vaccine design

Andreas Handel et al. PLoS Comput Biol. .

Abstract

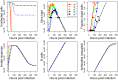
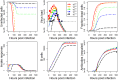
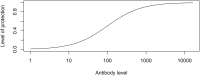
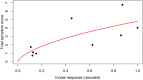
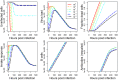
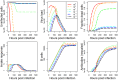
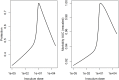
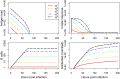
Vaccination is an effective method to protect against infectious diseases. An important consideration in any vaccine formulation is the inoculum dose, i.e., amount of antigen or live attenuated pathogen that is used. Higher levels generally lead to better stimulation of the immune response but might cause more severe side effects and allow for less population coverage in the presence of vaccine shortages. Determining the optimal amount of inoculum dose is an important component of rational vaccine design. A combination of mathematical models with experimental data can help determine the impact of the inoculum dose. We illustrate the concept of using data and models to inform inoculum dose determination for vaccines, wby fitting a mathematical model to data from influenza A virus (IAV) infection of mice and human parainfluenza virus (HPIV) infection of cotton rats at different inoculum doses. We use the model to map inoculum dose to the level of immune protection and morbidity and to explore how such a framework might be used to determine an optimal inoculum dose. We show how a framework that combines mathematical models with experimental data can be used to study the impact of inoculum dose on important outcomes such as immune protection and morbidity. Our findings illustrate that the impact of inoculum dose on immune protection and morbidity can depend on the specific pathogen and that both protection and morbidity do not necessarily increase monotonically with increasing inoculum dose. Once vaccine design goals are specified with required levels of protection and acceptable levels of morbidity, our proposed framework can help in the rational design of vaccines and determination of the optimal amount of inoculum.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Fit of model to IAV infection data at five different inoculum doses.
Kinetics for 6 of the seven model compartments for the best fit model are plotted. Since infected cells kinetics very closely follows virus kinetics, we did not plot it. Dashed horizontal line indicates the limit of detection for virus load. Best fit parameter values are provided in S1 Text. Data was available for virus load and cell damage. Virus load data was reported as hemagglutination units and cell damage was reported as percent lung cells that are pathological. Model virus load is in the same units as the experimental data. All other model quantities are in units of numbers. Damage in the model is measured as number of dead cells. Both dead cells and antibodies are rescaled as described in the method section to allow comparison between model and data. The plot shows the rescaled quantities.
Fig 2
Fig 2. Fit of model to HPIV infection data at five different inoculum doses.
Kinetics for 6 of the seven model compartments for the best fit model are plotted. Since infected cells kinetics very closely follows virus kinetics, we did not plot it. Dashed horizontal line indicates the limit of detection for virus load. Best fit parameter values are provided in S1 Text. Data was available for virus load and some antibody levels. Virus load data was reported as plaque forming units per gram of lung and antibody titer was reported as plaque reduction neutralization units. Model virus load is in the same units as the experimental data. All other model quantities are in units of numbers. Damage in the model is measured as number of dead cells. Both dead cells and antibodies are rescaled as described in the method section to allow comparison between model and data. The plot shows the rescaled quantities.
Fig 3
Fig 3. Protection as function of antibody levels (k1 = 1, k2 = log(100)).
Protection is the fraction of individuals in a population who are protected by the vaccine for a given level of antibodies. Antibody levels are on an arbitrary unit.
Fig 4
Fig 4. Data and best fit model for the connection between immune response and symptoms.
The innate response is the scaled sum of IFN-a, IL6, IL8, and TNF-a, symptoms are the total symptom score, both quantities are from [28]. The line shows the best fit provided by the equation mapping innate response to symptoms/morbidity.
Fig 5
Fig 5. IAV model simulation for a range of inoculum doses.
All plot settings are the same as described for Fig 1.
Fig 6
Fig 6. HPIV model simulation for a range of inoculum doses.
All plot settings are the same as described for Fig 2.
Fig 7
Fig 7. Inoculum dependent protection and damage for the IAV infection model.
Protection was determined based on antibody levels predicted by the model and computed using the equation for protection, P(A), described above. Morbidity was determined from the innate response levels predicted by the model and computed using the MAUC equation described above. To allow for better comparison with protection, we also scaled the MAUC values by their maximum.
Fig 8
Fig 8. Inoculum dependent protection and damage for the HPIV infection model.
Protection was determined based on antibody levels predicted by the model and computed using the equation for protection, P(A), described above. Morbidity was determined from the innate response levels predicted by the model and computed using the MAUC equation described above. To allow for better comparison with protection, we also scaled the MAUC values by their maximum.
Fig 9
Fig 9. Model for non-replicating vaccine.
Model parameters were set to dV = 0.1, kA'=1E-5, hV = 1E5, gF = 1E3, Fmax = 1E3, hF = 100, gB = 0.1, rA = 1, dA = 1E − 6, kA = 1E − 6. Initial conditions are F = 1, B = 1, A = 0 and varying values for antigen load.
Fig 10
Fig 10. Inoculum dependent protection and damage for the inactivated vaccine model.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Ada G. Overview of vaccines and vaccination. Molecular biotechnology. 2005;29: 255–272. 10.1385/MB:29:3:255 - DOI - PMC - PubMed
    1. Marois I, Cloutier A, Garneau É, Richter MV. Initial infectious dose dictates the innate, adaptive, and memory responses to influenza in the respiratory tract. Journal of leukocyte biology. 2012;92: 107–121. 10.1189/jlb.1011490 - DOI - PubMed
    1. Falsey AR. Half-dose influenza vaccine: Stretching the supply or wasting it? Archives of internal medicine. 2008;168: 2402–2403. 10.1001/archinte.168.22.2402 - DOI - PubMed
    1. Monath TP, Woodall JP, Gubler DJ, Yuill TM, Mackenzie JS, Martins RM, et al. Yellow fever vaccine supply: A possible solution. Lancet (London, England). 2016;387: 1599–1600. 10.1016/S0140-6736(16)30195-7 - DOI - PubMed
    1. Crotty S, Ahmed R. Immunological memory in humans. Seminars in Immunology. 2004;16: 197–203. 10.1016/j.smim.2004.02.008 - DOI - PubMed

Publication types