Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Jun 15;7(6):1481-1487.
doi: 10.1021/acssynbio.7b00442. Epub 2018 May 14.

Homogeneous Time Constants Promote Oscillations in Negative Feedback Loops

Franco Blanchini  1 , Christian Cuba Samaniego  2 , Elisa Franco  2 , Giulia Giordano  3
Affiliations

Homogeneous Time Constants Promote Oscillations in Negative Feedback Loops

Franco Blanchini et al. ACS Synth Biol. .

Abstract

Biological oscillators are present in nearly all self-regulating systems, from individual cells to entire organisms. In any oscillator structure, a negative feedback loop is necessary, but not sufficient to guarantee the emergence of periodic behaviors. The likelihood of oscillations can be improved by careful tuning of the system time constants and by increasing the loop gain, yet it is unclear whether there is any general relationship between optimal time constants and loop gain. This issue is particularly relevant in genetic oscillators resulting from a chain of different subsequent biochemical events, each with distinct (and uncertain) kinetics. Using two families of genetic oscillators as model examples, we show that the loop gain required for oscillations is minimum when all elements in the loop have the same time constant. On the contrary, we show that homeostasis is ensured if a single element is considerably slower than the others.

Keywords: biomolecular oscillators; delays; feedback; oscillations; synthetic biology; time constants.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interest.

Figures

Figure 1
Figure 1
Loop of n first order systems: block diagram.
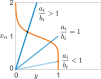
Figure 2
Figure 2
Goodwin oscillator: equilibrium conditions for different ratios ai/bi. The orange line represents the first expression in eq 8, while the blue lines represent the second expression in eq 8 for different values of the ratios ai/bi. Their intersections give, on the vertical axis, the equilibrium values of xn for various choices of ai/bi.
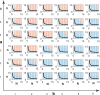
Figure 3
Figure 3
Oscillatory domain of the Goodwin oscillator with K = 1 in the (n, N) plane, for various choices of homogeneous rates, ai = a and bi = b for all i. The black line represents formula image; hence, eq 6 is satisfied in the whole region above. We compute the solutions of eq 9: red dots indicate an oscillatory behavior, blue dots indicate no oscillations, while gray dots indicate that no equilibrium can be found computationally due to numerical problems.
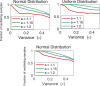
Figure 4
Figure 4
The fraction of oscillating samples of the Goodwin oscillator is largest when randomly drawn degradation rates are homogeneous. We simulated the model with K = 1 and n = 5; in the top panels N = 8, while in the bottom panel N = 10. We took ai = a and randomly generated rates bi with expected value E[bi] = 1 and variance ϵ. (In each simulation, the randomly generated parameters are kept constant during all the integration steps of the ODEs.) We show the fraction of oscillating samples as a function of the variance ϵ when the rates bi are taken from a normal distribution (top left, and bottom) and a uniform distribution (top right). In all panels, 1000 parameter samples are drawn per data point.
Figure 5
Figure 5
Oscillatory regime of the two-node oscillator. We compute the solutions of eq 15, with α1 = α2 = α, β1 = β2 = β, γ1 = γ2 = 1, δ1 = δ2 = 1 and K1 = K2 = 1, and indicate with red dots an oscillatory behavior, with blue dots no oscillations. Parameter sets that give rise to oscillations cannot be found for N = 2, while they are easy to find for N > 2.
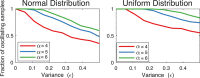
Figure 6
Figure 6
The fraction of oscillating samples of the two-node oscillator is largest when randomly drawn degradation rates are homogeneous. We simulated the model with N = 3, γ1 = γ2 = 1, K1 = K2 = 1, α1 = α2 = α and randomly generated (βi, δi) with expected value E[(βi, δi)] = (1, 1) and variance ϵ. (In each simulation, the randomly generated parameters are kept constant during all the integration steps of the ODEs.) We show the fraction of oscillating samples as a function of the variance ϵ when (βi, δi) are taken from a normal distribution (left) and a uniform distribution (right). 1000 parameter samples are drawn per data point.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Harrisingh M. C.; Nitabach M. N. (2008) Integrating circadian timekeeping with cellular physiology. Science 320 (5878), 879–880. 10.1126/science.1158619. - DOI - PubMed
    1. Pomerening J. R.; Sontag E. D.; Ferrell J. E. (2003) Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat. Cell Biol. 5 (4), 346–351. 10.1038/ncb954. - DOI - PubMed
    1. Nakajima M.; Imai K.; Ito H.; Nishiwaki T.; Murayama Y.; Iwasaki H.; et al. (2005) Reconstitution of Circadian Oscillation of Cyanobacterial KaiC Phosphorylation in Vitro. Science 308 (5720), 414–415. 10.1126/science.1108451. - DOI - PubMed
    1. O’Neill J. S.; Maywood E. S.; Chesham J. E.; Takahashi J. S.; Hastings M. H. (2008) cAMP-dependent signaling as a core component of the mammalian circadian pacemaker. Science 320 (5878), 949–953. 10.1126/science.1152506. - DOI - PMC - PubMed
    1. Pokhilko A.; Fernandez A. P.; Edwards K. D.; Southern M. M.; Halliday K. J.; Millar A. J. (2012) The clock gene circuit in Arabidopsis includes a repressilator with additional feedback loops. Mol. Syst. Biol. 8, 574.10.1038/msb.2012.6. - DOI - PMC - PubMed

Publication types

LinkOut - more resources