Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Mar;45(3):1178-1190.
doi: 10.1002/mp.12763. Epub 2018 Feb 19.

Automated mammographic breast density estimation using a fully convolutional network

Juhun Lee  1 , Robert M Nishikawa  1
Affiliations

Automated mammographic breast density estimation using a fully convolutional network

Juhun Lee et al. Med Phys. 2018 Mar.

Abstract

Purpose: The purpose of this study was to develop a fully automated algorithm for mammographic breast density estimation using deep learning.

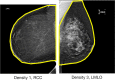
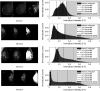
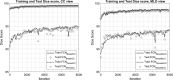
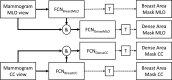
Method: Our algorithm used a fully convolutional network, which is a deep learning framework for image segmentation, to segment both the breast and the dense fibroglandular areas on mammographic images. Using the segmented breast and dense areas, our algorithm computed the breast percent density (PD), which is the faction of dense area in a breast. Our dataset included full-field digital screening mammograms of 604 women, which included 1208 mediolateral oblique (MLO) and 1208 craniocaudal (CC) views. We allocated 455, 58, and 91 of 604 women and their exams into training, testing, and validation datasets, respectively. We established ground truth for the breast and the dense fibroglandular areas via manual segmentation and segmentation using a simple thresholding based on BI-RADS density assessments by radiologists, respectively. Using the mammograms and ground truth, we fine-tuned a pretrained deep learning network to train the network to segment both the breast and the fibroglandular areas. Using the validation dataset, we evaluated the performance of the proposed algorithm against radiologists' BI-RADS density assessments. Specifically, we conducted a correlation analysis between a BI-RADS density assessment of a given breast and its corresponding PD estimate by the proposed algorithm. In addition, we evaluated our algorithm in terms of its ability to classify the BI-RADS density using PD estimates, and its ability to provide consistent PD estimates for the left and the right breast and the MLO and CC views of the same women. To show the effectiveness of our algorithm, we compared the performance of our algorithm against a state of the art algorithm, laboratory for individualized breast radiodensity assessment (LIBRA).

Result: The PD estimated by our algorithm correlated well with BI-RADS density ratings by radiologists. Pearson's rho values of our algorithm for CC view, MLO view, and CC-MLO-averaged were 0.81, 0.79, and 0.85, respectively, while those of LIBRA were 0.58, 0.71, and 0.69, respectively. For CC view and CC-MLO averaged cases, the difference in rho values between the proposed algorithm and LIBRA showed statistical significance (P < 0.006). In addition, our algorithm provided reliable PD estimates for the left and the right breast (Pearson's ρ > 0.87) and for the MLO and CC views (Pearson's ρ = 0.76). However, LIBRA showed a lower Pearson's rho value (0.66) for both the left and right breasts for the CC view. In addition, our algorithm showed an excellent ability to separate each sub BI-RADS breast density class (statistically significant, p-values = 0.0001 or less); only one comparison pair, density 1 and density 2 in the CC view, was not statistically significant (P = 0.54). However, LIBRA failed to separate breasts in density 1 and 2 for both the CC and MLO views (P > 0.64).

Conclusion: We have developed a new deep learning based algorithm for breast density segmentation and estimation. We showed that the proposed algorithm correlated well with BI-RADS density assessments by radiologists and outperformed an existing state of the art algorithm.

Keywords: breast density; deep learning; mammography; segmentation.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Two undergrad research assistants delineated the breast area on mammograms using a GUI program in MATLAB. Created breast ground truth masks include only the breast area, removing the pectoral muscle, as shown in the right image, and/or belly tissue, as shown in the left image. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 2
Figure 2
This figure shows a few examples from each density level and mammographic view on how we established the ground truth mask for dense fibroglandular area. Images on the left side of the panel show the original mammograms. Images in the middle show the results after applying manually delineated breast area mask and skin removal using a binary image erosion technique. Then, we applied a thresholding method to get ground truth mask for dense fibroglandular area. We used the midpoint of quartiles, that is, 12.5, 37.5, 62.5, and 87.5 percentiles, of pixel intensity distribution as thresholds. Then, we assigned any pixels higher than a given threshold as dense fibroglandular area. Note that we selected thresholds in descending order based on each case's BI‐RADS density level. For example, we selected the 87.5 percentile as the threshold for BI‐RADS density level 1 cases. Images on the right side of the panel show the results after applying the thresholding method. Also shown are the pixel intensity histograms inside the breast area.
Figure 3
Figure 3
This figure shows the testing scores, that is, Dice coefficient ranged [0, 100], for four FCN networks during the courses of training. Using the test dataset (N = 58 exams, that is, 116 MLO and CC view mammograms) we tested each network every 100 iterations of training. The plots include the Dice coefficient values for the training dataset (N = 455 exams, that is, 910 MLO and CC view mammograms). FCN networks for breast areas quickly converges to 98–99 after 1000 iterations for both the training and testing datasets. FCNs for dense areas relatively slow to converge compared to FCNs for breast areas, with the maximum Dice score for 94–95 after 4000 or 6000 iterations for both the training and testing datasets. We used the version of FCNs for breast areas at iteration 4000, and the version of FCNs for dense areas at iteration 8000 for this study.
Figure 4
Figure 4
This diagram summarizes the entire process of training, denoted as bold arrow lines, for the proposed algorithms, and how they create estimated breast area and dense area segmentations, denoted as dashed arrow lines. T refers to the thresholding to convert an estimated segmentation outcome in probability to binary masks. We used 0.5 for T. For breast area segmentation, we selected the largest blob in the resulting binary mask as breast area mask.
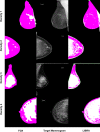
Figure 5
Figure 5
This figure shows some examples of breast area and dense area segmentation for the proposed algorithm and LIBRA. Images in 1st and 3rd columns show the outcomes of the proposed algorithm and those of LIBRA, respectively. Images in the center show the target mammograms. [Color figure can be viewed at wileyonlinelibrary.com]
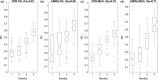
Figure 6
Figure 6
This figure shows the box plots of the proposed algorithm and LIBRA for the estimated PD values vs the BI‐RADS breast densities. The number of exams in each breast density category (density 1–4) are 15, 22, 28, and 26, respectively. The two extreme values on the box plots indicate the 25th and 75th percentile of the data. The two extreme values of the dash lines refer to the minimum and the maximum of the data that are not considered outliers. The plus (+) marker indicates a possible outlier within the data (which is more than 2.7 standard deviations above or below the mean of a normal distribution). The notches indicate the 95% confidence interval of the median.
Figure 7
Figure 7
This figure shows the box plots of the proposed algorithm and LIBRA for the case‐based PD value, that is, MLO and CC view averaged, vs BI‐RADS breast density. The number of exams in each breast density category (density 1–4) is 15, 22, 28, and 26, respectively. The proposed algorithm showed higher correlation between the PD estimates and the BI‐RADS density levels than LIBRA.
Figure 8
Figure 8
(a) and (c) show the Bland–Altman plot between the PD values of the left and right breasts for the proposed algorithm on MLO and CC views, respectively. Similarly, (b) and (d) show the Bland–Altman plots for LIBRA. (e) and (f) show the Bland–Altman plot between the PD estimates of CC and MLO views for the proposed algorithm and LIBRA, respectively. Note that the validation dataset (N = 91 exams, that is, 182 CC and MLO view mammograms) was used for this analysis. Both proposed and LIBRA showed no systematical bias (mean difference < 0.02) between measures, except LIBRA for the PD estimates between the CC and MLO views (mean difference = −0.082), that is, LIBRA overestimated PD estimates of the CC view compared to that of the MLO view. However, LIBRA showed wider variations in PD estimate differences than the proposed algorithm for all comparisons. The proposed algorithm showed high correlation (ρ > 0.87) between left and right PD value estimates for both MLO and CC views, while LIBRA showed only moderate correlation (ρ = 0.66) between left and right PD value estimates for CC views.
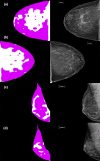
Figure 9
Figure 9
This figure shows outliers that the proposed algorithm either oversegmented (a)–(b) or undersegmented (c)–(d) dense fibroglandular areas of the breast. (a) and (b) are the right and left CC mammogram views from the same woman with a BI‐RADS density level 1. (c) and (d) are the right MLO mammogram views of two different women with a BI‐RADS density level 4. [Color figure can be viewed at wileyonlinelibrary.com]
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Tabár L, Vitak B, Chen HH, Yen MF, Duffy SW, Smith RA. Beyond randomized controlled trials: organized mammographic screening substantially reduces breast carcinoma mortality. Cancer. 2001;91:1724–1731. - PubMed
    1. Mandelson MT, Oestreicher N, Porter PL, et al. Breast density as a predictor of mammographic detection: comparison of interval‐ and screen‐detected cancers. J Natl Cancer Inst. 2000;92:1081–1087. - PubMed
    1. Boyd NF, Guo H, Martin LJ, et al. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007;356:227–236. - PubMed
    1. Yaghjyan L, Colditz GA, Collins LC, et al. Mammographic breast density and subsequent risk of breast cancer in postmenopausal women according to tumor characteristics. J Natl Cancer Inst. 2011;103:1179–1189. - PMC - PubMed
    1. Sickles EA, D'Orsi CJ, Bassett LW. ACR BI‐RADS® mammography. In: D'Orsi CJ, eds. ACR BI‐RADS® Atlas: Breast Imaging Reporting and Data System. Reston, VA: American College of Radiology; 2013.