Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Sep;80(3):1178-1188.
doi: 10.1002/mrm.27083. Epub 2018 Jan 15.

A bayesian method for accelerated magnetic resonance elastography of the liver

Christopher Ebersole  1   2 , Rizwan Ahmad  3 , Adam V Rich  1 , Lee C Potter  1 , Huiming Dong  2   3 , Arunark Kolipaka  1   2   3
Affiliations

A bayesian method for accelerated magnetic resonance elastography of the liver

Christopher Ebersole et al. Magn Reson Med. 2018 Sep.

Abstract

Purpose: Magnetic resonance elastography (MRE) is a noninvasive tool for quantifying soft tissue stiffness. MRE has been adopted as a clinical method for staging liver fibrosis. The application of liver MRE, however, requires multiple lengthy breath holds. We propose a new data acquisition and processing method to reduce MRE scan time.

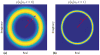
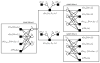
Theory and Methods: A Bayesian image reconstruction method that utilizes transform sparsity and magnitude consistency across different phase offsets to recover images from highly undersampled data is proposed. The method is validated using retrospectively downsampled phantom data and prospectively downsampled in vivo data (n=86).

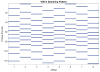
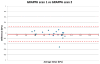
Results: The proposed technique allows accurate quantification of mean liver stiffness up to an acceleration factor of R=6, enabling acquisition of a slice in 4.3 seconds. Bland Altman analysis indicates that the proposed technique (R=6) has a bias of −0.04 kPa and limits of agreement of –0.36 to +0.28 kPa when compared to traditional GRAPPA reconstruction (R=1.4).

Conclusion: By exploiting transform sparsity and magnitude consistency, accurate quantification of mean stiffness in the liver can be obtained at acceleration rate of up to R=6. This potentially enables collection of three to four liver slices, as per clinical protocol, within a single breath hold.

Keywords: Bayesian model; MRI; compressive sensing; elastography; factor graph; liver MRE.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Example VISTA sampling pattern for 128 phase encodes and R = 11.6. The pattern is generated in the integrated offset-ky domain.
Figure 2
Figure 2
Mixture density relating offset xj to the reference offset x0. (a) The conditional distribution that enforces weak magnitude consistency, accommodating large magnitude variations across offsets, for example, due to dephasing. (b) The conditional distribution that enforces strong magnitude constraint, permitting little variation in magnitude. BEAM automatically assigns the probability that a given pixel belongs to v = 0 or v = 1 and enforces appropriate contributions from the two components of the mixture density.
Figure 3
Figure 3
Factor graph representation of the joint posterior distribution of an MRE dataset with three offsets. This structure is expandable to an arbitrary number of offsets, retaining this structure which relates each offset to the reference offset x0. Application of an iterative message passing algorithm provides a computationally efficient method of estimating the posterior marginal distribution of variables of interest. GAMP permits rapid estimation of messages passed in the densely interconnected loopy regions of the graph, which represent each offset.
Figure 4
Figure 4
Comparison of SENSE, SENSE-R, SCS, SL2, and BEAM phantom reconstructions at R = 6 and R = 12. Magnitude images, wave images, and elastograms are shown for each reconstruction.
Figure 5
Figure 5
Quantitative reconstruction metrics of SENSE, SENSE-R, SCS, SL2, and BEAM phantom reconstructions. (a) NMSE of reconstructed images, providing a measure of the error between each complex reconstruction and the fully sampled SENSE reconstruction. (b) Mean stiffness from ROI.
Figure 6
Figure 6
Comparison of GRAPPA at R = 1.4 and BEAM at R = 1, 4, 6, and 8 reconstructions of a prospectively accelerated in vivo dataset.
Figure 7
Figure 7
Bland Altman analysis of BEAM-derived stiffness measurements to GRAPPA-derived stiffness measurements. (a) Comparison of GRAPPA, R = 1.4, and BEAM, R = 1. (b) Comparison of GRAPPA, R = 1.4, and BEAM, R = 4. (c) Comparison of GRAPPA, R = 1.4, and BEAM, R = 6. (d) Comparison of GRAPPA, R = 1.4, and BEAM, R = 8.
Figure 8
Figure 8
Bland Altman analysis of stiffness measurements derived from two separate GRAPPA scans. The two GRAPPA scans were collected from the same volunteer using identical parameters but under separate breath holds.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Muthupillai R, Lomas D, Rossman P, Greenleaf J, Manduca A, Ehman R. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science (80-) 1995;269:1854–1857. doi: 10.1126/science.7569924. - DOI - PubMed
    1. Mariappan YK, Glaser KJ, Ehman RL. Magnetic resonance elastography: A review. Clin Anat. 2010;23:497–511. doi: 10.1002/ca.21006. - DOI - PMC - PubMed
    1. Gharib AM, Ai M, Han T, et al. Magnetic Resonance Elastography Shear Wave Velocity Correlates with Liver Fibrosis and Hepatic Venous Pressure Gradient in Adults with Advanced Liver Disease. 2017 - PMC - PubMed
    1. Low G, Kruse SA, Lomas DJ. General review of magnetic resonance elastography. World J Radiol. 2016;8:59–72. doi: 10.4329/wjr.v8.i1.59. - DOI - PMC - PubMed
    1. Huwart L, Sempoux C, Vicaut E, et al. Magnetic Resonance Elastography for the Noninvasive Staging of Liver Fibrosis. Gastroenterology. 2008;135:32–40. doi: 10.1053/j.gastro.2008.03.076. - DOI - PubMed

Publication types