Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Jan 10;9(1):136.
doi: 10.1038/s41467-017-02469-1.

Membrane shape-mediated wave propagation of cortical protein dynamics

Zhanghan Wu  1 , Maohan Su  2 , Cheesan Tong  2 , Min Wu  3 , Jian Liu  4
Affiliations

Membrane shape-mediated wave propagation of cortical protein dynamics

Zhanghan Wu et al. Nat Commun. .

Abstract

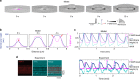
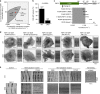
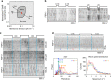
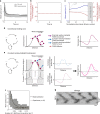
Immune cells exhibit stimulation-dependent traveling waves in the cortex, much faster than typical cortical actin waves. These waves reflect rhythmic assembly of both actin machinery and peripheral membrane proteins such as F-BAR domain-containing proteins. Combining theory and experiments, we develop a mechanochemical feedback model involving membrane shape changes and F-BAR proteins that render the cortex an interesting dynamical system. We show that such cortical dynamics manifests itself as ultrafast traveling waves of cortical proteins, in which the curvature sensitivity-driven feedback always constrains protein lateral diffusion in wave propagation. The resulting protein wave propagation mainly reflects the spatial gradient in the timing of local protein recruitment from cytoplasm. We provide evidence that membrane undulations accompany these protein waves and potentiate their propagation. Therefore, membrane shape change and protein curvature sensitivity may have underappreciated roles in setting high-speed cortical signal transduction rhythms.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interests.

Figures

Fig. 1
Fig. 1
Cortical protein oscillation underlies wave initiation and propagation. a Key model components and their interactions. b Model prediction that a localized GTP-Cdc42 pulse results in nucleation of a cortical patch. In the simulation shown, this external activation was transient, i.e., after 5 s it was turned off for the rest of the simulation. Top: temporal and spatial profiles of the initial Cdc42 activation. Bottom: spatial-temporal evolution of Cdc42 cortical density. c Model prediction that oscillation of cortical protein requires a threshold activation level. d Local cortical protein oscillation during wave propagation. Left: the model prediction of the time curves of F-BAR and actin oscillation at the epicenter, indicated by a cyan box in Fig. 1b, bottom. Right: experimental results show similar oscillations of cortical proteins. e Characteristics of wave propagation. Left: model prediction. Right: experimental measurement. Top: stable phase shift in the cortical oscillation between neighboring areas. The locations are marked by blue squares and green squares in the corresponding cases, in which they are 2.5 μm apart in model result (left bottom) and 2.88 μm apart in experiment (right bottom). The two ROIs are chosen to show that oscillations at the different locations have a stable phase shift, a feature that holds for any two ROIs along the direction of wave propagation. Bottom: snapshots of F-BAR cortical density profiles over time. For the model result, the time is relative to when the transient Cdc42 activation stops in Fig. 1b. In the experiment, the F-BAR level is the FBP17 fluorescence intensity minus background fluorescence, normalized by the maximum fluorescence
Fig. 2
Fig. 2
Membrane shape changes accompany traveling wave propagation. a Model predicts that the local membrane shape correlates with the F-BAR cortical density at the wavefront during wave propagation. The grayish meshes represent the membrane shapes in three-dimensional space (X, Y, Z) with a perspective angle; the inverted density maps are the corresponding F-BAR densities on the membrane, which is projected onto the two-dimensional X–Y plane. The scale bar for the x–y dimension is 5 μm and for the z-dimension is 200 nm. For the purpose of demonstration, the snapshots in Fig. 2a only show a part of the simulated membrane patch. The wave propagates beyond the domain defined in the snapshots until it approaches the boundary of the membrane patch; there, the wave subsides and eventually disappears, as the local membrane is clamped (Supplementary Movie 2 and Supplementary Fig. 2). b A zoom-in view of the local cortical rhythm along the magenta dash line across the cortex marked in Fig. 2a at t = 0, 2, and 4 s. Blue lines: local membrane shape. Magenta lines: F-BAR cortical level. The red arrows mark the locations with the largest membrane curvature. c Model prediction on temporal evolutions of the local F-BAR cortical level, membrane height, and rate of membrane height changes (dh/dt) at the location of the magenta square in Fig. 2a. d Experimental measurement of the spatial-temporal changes in F-BAR cortical level (by TIRFM) and membrane height (by SRIC) during traveling wave propagation. Left: kymographs of the local F-BAR cortical level and the corresponding relative membrane height. Right: time curves representing the local F-BAR cortical level, membrane height, and the rate of membrane height changes (dh/dt) at a fixed location. From SRIC measurements, we estimate the maximum membrane height to be ~140 nm (Supplementary Fig. 3). Note that this number is a very rough estimate, as the refractive indexes both inside and outside of the cell may undergo variation, due to changes in salt concentration and the organelle proximity. We therefore used the normalized membrane height in the experimental plot to avoid systematic error
Fig. 3
Fig. 3
Wave propagation requires F-BAR and its curvature sensitivity. a Model phase diagram showing the dependence of traveling waves on a proper balance between the curvature-dependent F-BAR-recruitment rate and the characteristic membrane curvature that recruits F-BAR. The red dot represents the model parameter set that generated the nominal model results in Figs. 1 and 2. b Double knockdown (DKD) of FBP17 and CIP4 by shRNA causes a reduction (P = 0.0008, Student’s t-test) in the percentage of cells with active Cdc42 (CBD-GFP) waves (4 experiments with 39 cells in total), comparing to wild-type (WT) cells (14 experiments with 133 cells). Error bars: s.e.m. c F-BAR domain of FBP17 is replaced with other membrane-binding motifs. Ranges of curvature (radius−1) preferences of different membrane-binding domains are plotted, , , . Gray area indicates the curvature range that allows wave formation, corresponding to the gray area of a. d The curvature of F-BAR domain is critical for wave formation. A micrograph and a kymograph for each mutant protein both in WT and DKD conditions are shown. Only the mutant protein with an F-BAR (FCHo1) domain could rescue wave formation in DKD cells. e The ability of point mutants of F-BAR domain of FBP17 to localize to the waves in WT cells or rescue wave formation in DKD cells correlates with their tubulation activities in vitro. Representative kymographs of cells expressing point mutants or full-length construct of FBP17-GFP in WT cells and DKD cells are shown. Mutants are separated into four groups based on curvature-generating abilities. Scale bar: 10 μm
Fig. 4
Fig. 4
Membrane mechanics is essential for wave propagation. a Model phase diagram showing the dependence of traveling waves on the membrane tension and the F-BAR cortical recruitment rate. The red dot represents the model parameter set that generated the nominal model results in Fig. 2. b Osmotic shock reversibly inhibits traveling waves as shown by the FBP17-GFP kymographs. Cells were cyclically perfused with isotonic (300 mOsm) buffer for 100 s and hypotonic (30 mOsm) or hypertonic (600 mOsm) buffer for 25 s (Supplementary Movies 4 and 5). c Kymographs of FBP17-GFP show that surfactant deoxycholate (DC) reversibly inhibited traveling waves in a dose-dependent manner. Cells were cyclically perfused with isotonic buffer without DC for 100 s and isotonic buffer with DC at different concentrations (400, 200, and 100 μM, respectively) for 100 s. d Mild osmotic shock changes oscillation period but not wave speed. Top: kymograph of FBP17-GFP waves in a cell that was cyclically perfused with mild hyper-osmotic buffer for 250 s each duration. In duration a and c, the cell was perfused with 280 mOsm buffer, while in duration b and d, cells were perfused with 310 mOsm buffer. Bottom left: fast Fourier transform (FFT) shows the dominant periods in each duration. Bottom right: wave speed distribution in each duration. Colors of plots indicate durations as in top. For b–d all the schematics above kymographs illustrate putative changes in cell membrane tension. Scale bar: 10 μm
Fig. 5
Fig. 5
Curvature sensing-mediated cortical protein waves always reflect protein recruitment from cytoplasm onto membrane. a Time curve of wave speed. The analytic result was obtained by computing the analytical solution (Eq. (2.24)), in which we took the membrane shape at the wavefront from the full model simulation as the input, and fixed all the other parameters in the formula in accordance to the corresponding full model case. We note that there is one parameter in the analytic formula that cannot be analytically derived from the reaction rates in the full model. Instead, we can numerically determine the range of its value (Supplementary Note 2), which reflects on the gray zone in the analytic results. b Time curve of diffusional contribution to wave propagation. c Diffusion-dependence of wave propagation. b, c Relative diffusion contribution to wave propagation is defined as the ratio between the diffusion term and the reaction term in the dynamic equation of F-BAR (Eq. (1.3) of the full model, Supplementary Note 1). And we chose the location ahead of the wavefront, where the absolute value of membrane curvature is the highest. Variation in this location does not change the qualitative conclusions from these plots. d, e Schematics of curvature sensing-mediated inhibitory effects on diffusional contribution to wave propagation. d Traveling wave from conventional reaction-diffusion system. e Curvature sensing-driven traveling wave. In d the “h” represents a chemical concentration in a generic sense, whereas the “h” in e is the membrane height and ∇2h is the membrane curvature. The round disk represents a cortical protein “F”. We emphasize that the comparison here is only within the regime of traveling waves, not stationary wave phenomena that could emerge with characteristic spatial periodicities from conventional reaction-diffusion systems. f Inverse relationship between wave speed and the spatial gradient of cortical protein density at wavefront. The experimental data were collected from 37 waves in 8 cells. The F-BAR intensity for each wavefront was normalized to the maximum value within the individual cell. The gray shade represents the tracking measurement uncertainty (Supplementary Figs. 8 and 9). g Representative montage of FBP17 punctum during the apparent wave propagation show that each punctum assembles and disassembles at a fixed location
See this image and copyright information in PMC

Comment in

  • The Rise of Ultrafast Waves.
    Puls O, Yang Q. Puls O, et al. Dev Cell. 2018 Dec 3;47(5):532-534. doi: 10.1016/j.devcel.2018.11.026. Dev Cell. 2018. PMID: 30513294 Free PMC article.

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Winfree A. T. The Geometry of Biological Time, 2nd edn. Springer (2001).
    1. Allard J, Mogilner A. Traveling waves in actin dynamics and cell motility. Curr. Opin. Cell Biol. 2012;25:107–115. doi: 10.1016/j.ceb.2012.08.012. - DOI - PMC - PubMed
    1. Weiner OD, Marganski WA, Wu LF, Altschuler SJ, Kirschner MW. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. - DOI - PMC - PubMed
    1. Wu M, Wu X, De Camilli P. Calcium oscillations-coupled conversion of actin travelling waves to standing oscillations. Proc. Natl Acad. Sci. USA. 2013;110:1339–1344. doi: 10.1073/pnas.1221538110. - DOI - PMC - PubMed
    1. Baumgart T, Capraro BR, Zhu C, Das SL. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem. 2011;62:483–506. doi: 10.1146/annurev.physchem.012809.103450. - DOI - PMC - PubMed

Publication types

LinkOut - more resources