Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Jun 12;18(1):55.
doi: 10.1186/s12863-017-0519-1.

Detection of gene-environment interactions in the presence of linkage disequilibrium and noise by using genetic risk scores with internal weights from elastic net regression

Anke Hüls  1   2 , Katja Ickstadt  3 , Tamara Schikowski  4 , Ursula Krämer  4
Affiliations

Detection of gene-environment interactions in the presence of linkage disequilibrium and noise by using genetic risk scores with internal weights from elastic net regression

Anke Hüls et al. BMC Genet. .

Erratum in

Abstract

Background: For the analysis of gene-environment (GxE) interactions commonly single nucleotide polymorphisms (SNPs) are used to characterize genetic susceptibility, an approach that mostly lacks power and has poor reproducibility. One promising approach to overcome this problem might be the use of weighted genetic risk scores (GRS), which are defined as weighted sums of risk alleles of gene variants. The gold-standard is to use external weights from published meta-analyses.

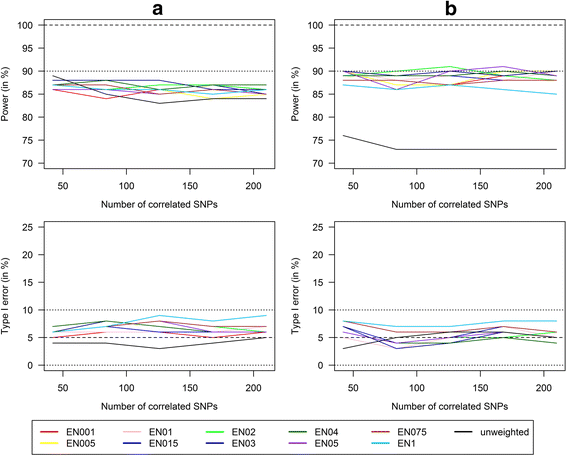
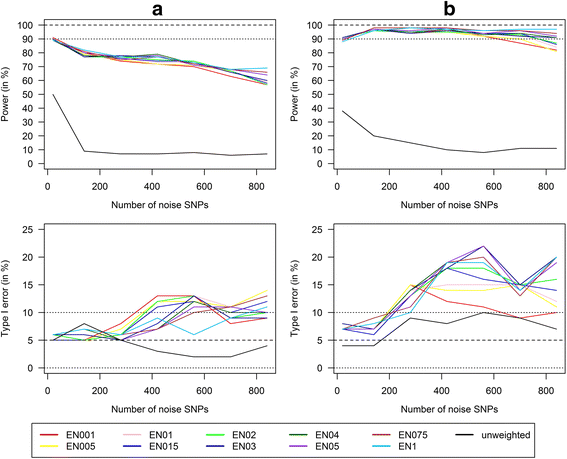
Methods: In this study, we used internal weights from the marginal genetic effects of the SNPs estimated by a multivariate elastic net regression and thereby provided a method that can be used if there are no external weights available. We conducted a simulation study for the detection of GxE interactions and compared power and type I error of single SNPs analyses with Bonferroni correction and corresponding analysis with unweighted and our weighted GRS approach in scenarios with six risk SNPs and an increasing number of highly correlated (up to 210) and noise SNPs (up to 840).

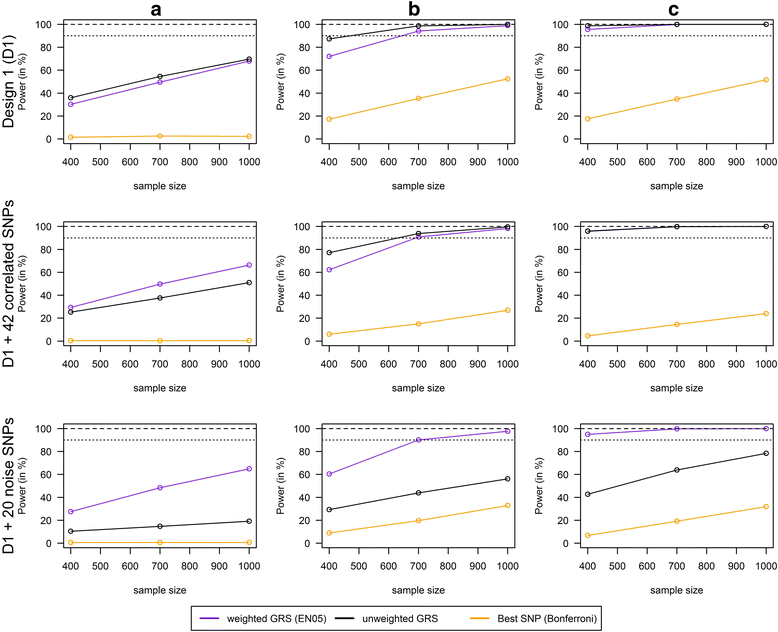
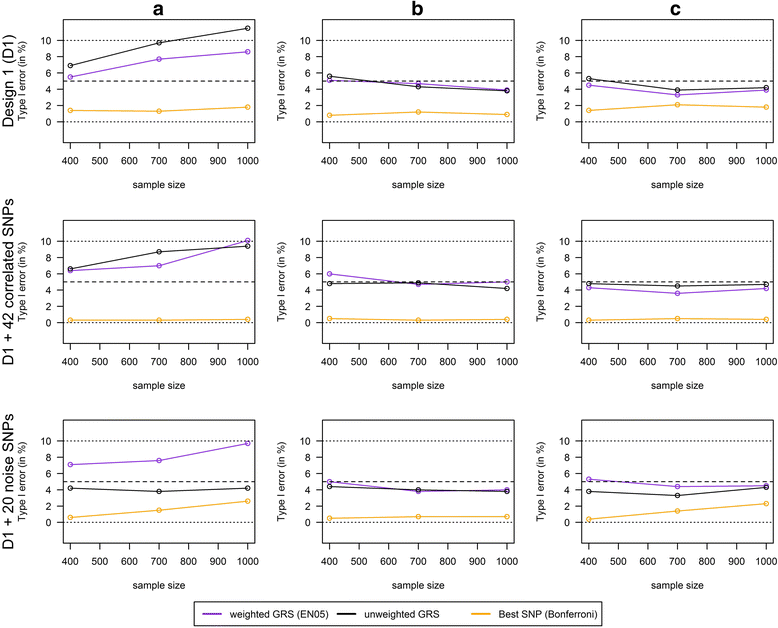
Results: Applying weighted GRS increased the power enormously in comparison to the common single SNPs approach (e.g. 94.2% vs. 35.4%, respectively, to detect a weak interaction with an OR ≈ 1.04 for six uncorrelated risk SNPs and n = 700 with a well-controlled type I error). Furthermore, weighted GRS outperformed the unweighted GRS, in particular in the presence of SNPs without any effect on the phenotype (e.g. 90.1% vs. 43.9%, respectively, when 20 noise SNPs were added to the six risk SNPs). This outperforming of the weighted GRS was confirmed in a real data application on lung inflammation in the SALIA cohort (n = 402). However, in scenarios with a high number of noise SNPs (>200 vs. 6 risk SNPs), larger sample sizes are needed to avoid an increased type I error, whereas a high number of correlated SNPs can be handled even in small samples (e.g. n = 400).

Conclusion: In conclusion, weighted GRS with weights from the marginal genetic effects of the SNPs estimated by a multivariate elastic net regression were shown to be a powerful tool to detect gene-environment interactions in scenarios of high Linkage disequilibrium and noise.

Keywords: Lasso; Linkage disequilibrium; Noise; Penalized regression model; Polygenic approach; Ridge regression.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Power of weighted/unweighted GRS and single SNPs analysis with increasing sample size. Power comparison for the combined analysis of interaction effects between 6 SNPs and a single continuous environmental exposure (Design 1 (D1)) and in two extended scenarios: 1) “D1 + 42 correlated SNPs” contains the 6 SNPs from Design 1 and 42 SNPs that are in a high Linkage Disequilibrium with these SNPs and 2) “D1 + 20 noise SNPs” contains the 6 SNPs from Design 1 and 20 SNPs that are not associated with the phenotype. Comparison of weighted GRS (weights from elastic net regression with penalty weight α = 0.5 (EN05)), unweighted GRS and single SNPs analysis with Bonferroni correction (best SNP; SNP with the smallest p-value) in scenarios with increasing effect size of the interaction term (a) Mean (OR(GxE) = 1.01, b) Mean OR(GxE) = 1.04, c) Mean OR(GxE) = 1.05) and increasing sample size of 400, 700 and 1000 (1000 replications)
Fig. 2
Fig. 2
Type I error of weighted/unweighted GRS and single SNPs analysis with increasing sample size. Power comparison for the combined analysis of interaction effects between 6 SNPs and a single continuous environmental exposure (Design 1 (D1)) and in two extended scenarios: 1) “D1 + 42 correlated SNPs” contains the 6 SNPs from Design 1 and 42 SNPs that are in a high Linkage Disequilibrium with these SNPs and 2) “D1 + 20 noise SNPs” contains the 6 SNPs from Design 1 and 20 SNPs that are not associated with the phenotype. Comparison of weighted GRS (weights from elastic net regression with penalty weight α = 0.5 (EN05)), unweighted GRS and single SNPs analysis with Bonferroni correction (best SNP; SNP with the smallest p-value) in scenarios with increasing effect size of the interaction term (a) Mean (OR(GxE) = 1.01, b) Mean OR(GxE) = 1.04, c) Mean OR(GxE) = 1.05) and increasing sample size of 400, 700 and 1000 (1000 replications)
Fig. 3
Fig. 3
Power/type I error of weighted/unweighted GRS with increasing number of correlated SNPs. Power and Type I error comparison for the combined analysis of interaction effects between 6 SNPs and a single continuous environmental exposure. Comparison of continuous weighted GRS with weights from the elastic net regression with varying penalty weight α (α = 0.01, 0.05, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.75, and 1; called EN001, EN005, …, EN1) and continuous unweighted GRS in different scenarios with increasing effect size of the interaction term (a) Mean OR(GxE) = 1.04 (n = 700), b) Mean OR(GxE) = 1.05 (n = 400)) and an increasing number of correlated SNPs that are in a high Linkage Disequilibrium with the 6 SNPs from Design 1 (from 42 to 210) (100 replications)
Fig. 4
Fig. 4
Power/type I error of weighted/unweighted GRS with increasing number of noise SNPs. Power and Type I error comparison for the combined analysis of interaction effects between 6 SNPs and a single continuous environmental exposure. Comparison of continuous weighted GRS with weights from the elastic net regression with varying penalty weight α (α = 0.01, 0.05, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.75, and 1; called EN001, EN005, …, EN1) and continuous unweighted GRS in different scenarios with increasing effect size of the interaction term (a) Mean OR(GxE) = 1.04 (n = 700), b) Mean OR(GxE) = 1.05 (n = 400)) and an increasing number of noise SNPs that are not associated with the phenotype (from 20 to 840) (100 replications)
Fig. 5
Fig. 5
Power/type I error of weighted GRS with 560 noise SNPs and increasing sample size. Power and Type I error comparison for the combined analysis of interaction effects between 6 SNPs and a single continuous environmental exposure. Comparison of continuous weighted GRS with weights from the elastic net regression with varying penalty weight α (α = 0.01, 0.05, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.75, and 1; called EN001, EN005, …, EN1) in different scenarios with increasing effect size of the interaction term (a) Mean OR(GxE) = 1.04, b) Mean OR(GxE) = 1.05) and an increasing sample size and 560 noise SNPs that are not associated with the phenotype (100 replications)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Ottman R. Gene-environment Interaction: definitions and study designs. Prev Med. 1996;25:764-70. doi: 10.1006/pmed.1996.0117. - DOI - PMC - PubMed
    1. Marigorta UM, Gibson G. A simulation study of gene-by-environment interactions in GWAS implies ample hidden effects. Front Genet. 2014;5:225. doi: 10.3389/fgene.2014.00225. - DOI - PMC - PubMed
    1. Salvatore JE, Aliev F, Edwards AC, Evans DM, Macleod J, Hickman M, et al. Polygenic scores predict alcohol problems in an independent sample and show moderation by the environment. Genes (Basel) 2014;5:330–346. - PMC - PubMed
    1. Purcell SM, Wray NR, Stone JL, Visscher PM, O’Donovan MC, Sullivan PF, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;72:1343–1354. - PMC - PubMed
    1. Paynter NP, Chasman DI, Pare G, Buring JE, Cook NR, Miletich JP, et al. Association between a literature-based genetic risk score and cardiovascular events in women. J Am Med Assoc. 2010;303:631–637. doi: 10.1001/jama.2010.119. - DOI - PMC - PubMed

Publication types

Substances

LinkOut - more resources