Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Jul 11;13(7):3378-3387.
doi: 10.1021/acs.jctc.7b00336. Epub 2017 Jun 7.

Acceleration of Linear Finite-Difference Poisson-Boltzmann Methods on Graphics Processing Units

Ruxi Qi  1 , Wesley M Botello-Smith  1 , Ray Luo  1
Affiliations

Acceleration of Linear Finite-Difference Poisson-Boltzmann Methods on Graphics Processing Units

Ruxi Qi et al. J Chem Theory Comput. .

Abstract

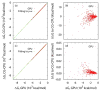
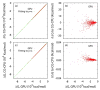
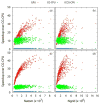
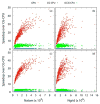
Electrostatic interactions play crucial roles in biophysical processes such as protein folding and molecular recognition. Poisson-Boltzmann equation (PBE)-based models have emerged as widely used in modeling these important processes. Though great efforts have been put into developing efficient PBE numerical models, challenges still remain due to the high dimensionality of typical biomolecular systems. In this study, we implemented and analyzed commonly used linear PBE solvers for the ever-improving graphics processing units (GPU) for biomolecular simulations, including both standard and preconditioned conjugate gradient (CG) solvers with several alternative preconditioners. Our implementation utilizes the standard Nvidia CUDA libraries cuSPARSE, cuBLAS, and CUSP. Extensive tests show that good numerical accuracy can be achieved given that the single precision is often used for numerical applications on GPU platforms. The optimal GPU performance was observed with the Jacobi-preconditioned CG solver, with a significant speedup over standard CG solver on CPU in our diversified test cases. Our analysis further shows that different matrix storage formats also considerably affect the efficiency of different linear PBE solvers on GPU, with the diagonal format best suited for our standard finite-difference linear systems. Further efficiency may be possible with matrix-free operations and integrated grid stencil setup specifically tailored for the banded matrices in PBE-specific linear systems.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Correlations (a), (c) and differences (b), (d) of electrostatic solvation energies on GPU (Jacobi with CUSP library and DIA matrix format) and on CPU (CG) for the protein test set. Free space boundary condition was used. The convergence criterion was set to 10−3 (a), (b) and 10−6 (c), (d). The linear regression slopes are 0.999931 and 0.999996 for 10−3 and 10−6 criterion respectively, and the correlation coefficients are 1.0 for both.
Figure 2
Figure 2
Correlations (a), (c) and differences (b), (d) of electrostatic solvation energies on GPU (Jacobi with CUSP library and DIA matrix format) and on CPU (CG) for the protein test set. The periodic boundary condition (PBC) was used. The convergence criterion was set to 10−3 (a), (b) and 10−6 (c), (d). The linear regression slopes are 0.999639 and 1.0 for 10−3 and 10−6 criterion respectively, and the correlation coefficients are 1.0 for both.
Figure 3
Figure 3
Comparison between PB solvers on GPU (Jacobi with CUSP library and DIA matrix format) and on CPU with free space boundary condition for the protein test set, as functions of number of atoms and grids respectively. The convergence criterion was set to 10−3 (a), (b) and 10−6 (c), (d).
Figure 4
Figure 4
Comparison between PB solvers on GPU (Jacobi with CUSP library and DIA matrix format) and on CPU (ICCG) with PBC for the protein test set, as functions of number of atoms and grids respectively. The convergence criterion was set to 10−3 (a), (b) and 10−6 (c), (d).
Figure 5
Figure 5
Average time used by different CPU and GPU solvers for selected test proteins. The detail of each solver combination is elaborated in Table 1. The GPU/ICCG solver is not listed due to their extremely long execution times. The convergence criterion was set to 10−3 (top) and 10−6 (bottom).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Davis ME, McCammon JA. ELECTROSTATICS IN BIOMOLECULAR STRUCTURE AND DYNAMICS. Chem Rev (Washington, DC, U S) 1990;90(3):509–521.
    2. Honig B, Sharp K, Yang AS. MACROSCOPIC MODELS OF AQUEOUS-SOLUTIONS - BIOLOGICAL AND CHEMICAL APPLICATIONS. J Phys Chem. 1993;97(6):1101–1109.
    3. Honig B, Nicholls A. CLASSICAL ELECTROSTATICS IN BIOLOGY AND CHEMISTRY. Science. 1995;268(5214):1144–1149. - PubMed
    4. Beglov D, Roux B. Solvation of complex molecules in a polar liquid: An integral equation theory. J Chem Phys. 1996;104(21):8678–8689.
    5. Cramer CJ, Truhlar DG. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem Rev (Washington, DC, U S) 1999;99(8):2161–2200. - PubMed
    6. Bashford D, Case DA. Generalized born models of macromolecular solvation effects. Annu Rev Phys Chem. 2000;51:129–152. - PubMed
    7. Baker NA. Improving implicit solvent simulations: a Poisson-centric view. Curr Opin Struct Biol. 2005;15(2):137–143. - PubMed
    8. Chen JH, Im WP, Brooks CL. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J Am Chem Soc. 2006;128(11):3728–3736. - PMC - PubMed
    9. Feig M, Chocholousova J, Tanizaki S. Extending the horizon: towards the efficient modeling of large biomolecular complexes in atomic detail. Theor Chem Acc. 2006;116(1–3):194–205.
    10. Koehl P. Electrostatics calculations: latest methodological advances. Curr Opin Struct Biol. 2006;16(2):142–151. - PubMed
    11. Im W, Chen JH, Brooks CL. Peptide and protein folding and conformational equilibria: Theoretical treatment of electrostatics and hydrogen bonding with implicit solvent models. Peptide Solvation and H-Bonds. 2006;72:173. - PubMed
    12. Lu BZ, Zhou YC, Holst MJ, McCammon JA. Recent progress in numerical methods for the Poisson-Boltzmann equation in biophysical applications. Communications in Computational Physics. 2008;3(5):973–1009.
    13. Wang J, Tan CH, Tan YH, Lu Q, Luo R. Poisson-Boltzmann solvents in molecular dynamics Simulations. Communications in Computational Physics. 2008;3(5):1010–1031.
    14. Altman MD, Bardhan JP, White JK, Tidor B. Accurate Solution of Multi-Region Continuum Biomolecule Electrostatic Problems Using the Linearized Poisson-Boltzmann Equation with Curved Boundary Elements. J Comput Chem. 2009;30(1):132–153. - PMC - PubMed
    15. Cai Q, Wang J, Hsieh M-J, Ye X, Luo R. Chapter Six - Poisson–Boltzmann Implicit Solvation Models. In: Ralph AW, editor. Annual Reports in Computational Chemistry. Vol. 8. Elsevier; 2012. pp. 149–162.
    16. Xiao L, Wang C, Luo R. Recent progress in adapting Poisson–Boltzmann methods to molecular simulations. Journal of Theoretical and Computational Chemistry. 2014;13(03):1430001.
    17. Botello-Smith WM, Cai Q, Luo R. Biological applications of classical electrostatics methods. Journal of Theoretical and Computational Chemistry. 2014;13(03):1440008.
    1. Warwicker J, Watson HC. Calculation of the Electric-Potential in the Active-Site Cleft Due to Alpha-Helix Dipoles. J Mol Biol. 1982;157(4):671–679. - PubMed
    2. Bashford D, Karplus M. Pkas Of Ionizable Groups In Proteins - Atomic Detail From A Continuum Electrostatic Model. Biochemistry. 1990;29(44):10219–10225. - PubMed
    3. Jeancharles A, Nicholls A, Sharp K, Honig B, Tempczyk A, Hendrickson TF, Still WC. Electrostatic Contributions To Solvation Energies - Comparison Of Free-Energy Perturbation And Continuum Calculations. J Am Chem Soc. 1991;113(4):1454–1455.
    4. Gilson MK. Theory of Electrostatic Interactions in Macromolecules. Curr Opin Struct Biol. 1995;5(2):216–223. - PubMed
    5. Edinger SR, Cortis C, Shenkin PS, Friesner RA. Solvation free energies of peptides: Comparison of approximate continuum solvation models with accurate solution of the Poisson-Boltzmann equation. J Phys Chem B. 1997;101(7):1190–1197.
    6. Lu Q, Luo R. A Poisson-Boltzmann dynamics method with nonperiodic boundary condition. J Chem Phys. 2003;119(21):11035–11047.
    7. Tan C, Yang L, Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. J Phys Chem B. 2006;110(37):18680–18687. - PubMed
    8. Cai Q, Wang J, Zhao HK, Luo R. On removal of charge singularity in Poisson-Boltzmann equation. J Chem Phys. 2009;130(14) - PubMed
    9. Ye X, Cai Q, Yang W, Luo R. Roles of Boundary Conditions in DNA Simulations: Analysis of Ion Distributions with the Finite-Difference Poisson-Boltzmann Method. Biophys J. 2009;97(2):554–562. - PMC - PubMed
    10. Ye X, Wang J, Luo R. A Revised Density Function for Molecular Surface Calculation in Continuum Solvent Models. J Chem Theory Comput. 2010;6(4):1157–1169. - PMC - PubMed
    11. Luo R, Moult J, Gilson MK. Dielectric screening treatment of electrostatic solvation. J Phys Chem B. 1997;101(51):11226–11236.
    12. Wang J, Tan C, Chanco E, Luo R. Quantitative analysis of Poisson-Boltzmann implicit solvent in molecular dynamics. Phys Chem Chem Phys. 2010;12(5):1194–1202. - PubMed
    13. Hsieh MJ, Luo R. Exploring a coarse-grained distributive strategy for finite-difference Poisson-Boltzmann calculations. J Mol Model. 2011;17(8):1985–1996. - PMC - PubMed
    14. Cai Q, Ye X, Wang J, Luo R. On-the-Fly Numerical Surface Integration for Finite-Difference Poisson-Boltzmann Methods. J Chem Theory Comput. 2011;7(11):3608–3619. - PMC - PubMed
    15. Botello-Smith WM, Liu X, Cai Q, Li Z, Zhao H, Luo R. Numerical Poisson-Boltzmann Model for Continuum Membrane Systems. Chem Phys Lett. 2012 - PMC - PubMed
    16. Liu X, Wang C, Wang J, Li Z, Zhao H, Luo R. Exploring a charge-central strategy in the solution of Poisson’s equation for biomolecular applications. Phys Chem Chem Phys. 2013 - PMC - PubMed
    17. Wang C, Wang J, Cai Q, Li ZL, Zhao H, Luo R. Exploring High Accuracy Poisson-Boltzmann Methods for Biomolecular Simulations. Computational and Theoretical Chemistry. 2013;1024:34–44. - PMC - PubMed
    1. Klapper I, Hagstrom R, Fine R, Sharp K, Honig B. Focusing of Electric Fields in the Active Site of Copper-Zinc Superoxide Dismutase Effects of Ionic Strength and Amino Acid Modification. Proteins Structure Function and Genetics. 1986;1(1):47–59. - PubMed
    2. Davis ME, McCammon JA. Solving the Finite-Difference Linearized Poisson-Boltzmann Equation - a Comparison of Relaxation and Conjugate-Gradient Methods. J Comput Chem. 1989;10(3):386–391.
    3. Nicholls A, Honig B. A Rapid Finite-Difference Algorithm, Utilizing Successive over-Relaxation to Solve the Poisson-Boltzmann Equation. J Comput Chem. 1991;12(4):435–445.
    4. Luty BA, Davis ME, McCammon JA. Solving the Finite-Difference Nonlinear Poisson-Boltzmann Equation. J Comput Chem. 1992;13(9):1114–1118.
    5. Holst M, Saied F. Multigrid Solution of the Poisson-Boltzmann Equation. J Comput Chem. 1993;14(1):105–113.
    6. Forsten KE, Kozack RE, Lauffenburger DA, Subramaniam S. Numerical-Solution of the Nonlinear Poisson-Boltzmann Equation for a Membrane-Electrolyte System. J Phys Chem. 1994;98(21):5580–5586.
    7. Holst MJ, Saied F. NUMERICAL-SOLUTION OF THE NONLINEAR POISSON-BOLTZMANN EQUATION - DEVELOPING MORE ROBUST AND EFFICIENT METHODS. J Comput Chem. 1995;16(3):337–364.
    8. Bashford D. An Object-Oriented Programming Suite for Electrostatic Effects in Biological Molecules. Lecture Notes in Computer Science. 1997;1343:233–240.
    9. Im W, Beglov D, Roux B. Continuum Solvation Model: computation of electrostatic forces from numerical solutions to the Poisson-Boltzmann equation. Comput Phys Commun. 1998;111(1–3):59–75.
    10. Rocchia W, Alexov E, Honig B. Extending the applicability of the nonlinear Poisson-Boltzmann equation: Multiple dielectric constants and multivalent ions. J Phys Chem B. 2001;105(28):6507–6514.
    11. Luo R, David L, Gilson MK. Accelerated Poisson-Boltzmann calculations for static and dynamic systems. J Comput Chem. 2002;23(13):1244–1253. - PubMed
    12. Wang J, Luo R. Assessment of Linear Finite-Difference Poisson-Boltzmann Solvers. J Comput Chem. 2010;31(8):1689–1698. - PMC - PubMed
    13. Cai Q, Hsieh MJ, Wang J, Luo R. Performance of Nonlinear Finite-Difference Poisson-Boltzmann Solvers. J Chem Theory Comput. 2010;6(1):203–211. - PMC - PubMed
    14. Botello-Smith WM, Luo R. Applications of MMPBSA to Membrane Proteins I: Efficient Numerical Solutions of Periodic Poisson–Boltzmann Equation. J Chem Inf Model. 2015;55(10):2187–2199. - PMC - PubMed
    1. Cortis CM, Friesner RA. Numerical solution of the Poisson-Boltzmann equation using tetrahedral finite-element meshes. J Comput Chem. 1997;18(13):1591–1608.
    2. Holst M, Baker N, Wang F. Adaptive multilevel finite element solution of the Poisson-Boltzmann equation I. Algorithms and examples. J Comput Chem. 2000;21(15):1319–1342.
    3. Baker N, Holst M, Wang F. Adaptive multilevel finite element solution of the Poisson-Boltzmann equation II. Refinement at solvent-accessible surfaces in biomolecular systems. J Comput Chem. 2000;21(15):1343–1352.
    4. Shestakov AI, Milovich JL, Noy A. Solution of the nonlinear Poisson-Boltzmann equation using pseudo-transient continuation and the finite element method. J Colloid Interface Sci. 2002;247(1):62–79. - PubMed
    5. Chen L, Holst MJ, Xu JC. The finite element approximation of the nonlinear Poisson-Boltzmann equation. SIAM Journal on Numerical Analysis. 2007;45:2298–2320.
    6. Xie D, Zhou S. A new minimization protocol for solving nonlinear Poisson–Boltzmann mortar finite element equation. BIT Numerical Mathematics. 2007;47(4):853–871.
    7. Wang J, Cieplak P, Li J, Wang J, Cai Q, Hsieh M, Lei H, Luo R, Duan Y. Development of Polarizable Models for Molecular Mechanical Calculations II: Induced Dipole Models Significantly Improve Accuracy of Intermolecular Interaction Energies. J Phys Chem B. 2011;115(12):3100–3111. - PMC - PubMed
    8. Lu B, Holst MJ, McCammon JA, Zhou YC. Poisson-Nernst-Planck equations for simulating biomolecular diffusion-reaction processes I: Finite element solutions. J Comput Phys. 2010;229(19):6979–6994. - PMC - PubMed
    9. Bond SD, Chaudhry JH, Cyr EC, Olson LN. A First-Order System Least-Squares Finite Element Method for the Poisson-Boltzmann Equation. J Comput Chem. 2010;31(8):1625–1635. - PubMed
    1. Miertus S, Scrocco E, Tomasi J. Electrostatic Interaction of a Solute with a Continuum - a Direct Utilization of Abinitio Molecular Potentials for the Prevision of Solvent Effects. Chem Phys. 1981;55(1):117–129.
    2. Hoshi H, Sakurai M, Inoue Y, Chujo R. Medium Effects on the Molecular Electronic-Structure .1. the Formulation of a Theory for the Estimation of a Molecular Electronic-Structure Surrounded by an Anisotropic Medium. J Chem Phys. 1987;87(2):1107–1115.
    3. Zauhar RJ, Morgan RS. The Rigorous Computation of the Molecular Electric-Potential. J Comput Chem. 1988;9(2):171–187.
    4. Rashin AA. Hydration Phenomena, Classical Electrostatics, and the Boundary Element Method. J Phys Chem. 1990;94(5):1725–1733.
    5. Yoon BJ, Lenhoff AM. A Boundary Element Method for Molecular Electrostatics with Electrolyte Effects. J Comput Chem. 1990;11(9):1080–1086.
    6. Juffer AH, Botta EFF, Vankeulen BAM, Vanderploeg A, Berendsen HJC. The Electric-Potential of a Macromolecule in a Solvent - a Fundamental Approach. J Comput Phys. 1991;97(1):144–171.
    7. Zhou HX. Boundary-Element Solution of Macromolecular Electrostatics - Interaction Energy between 2 Proteins. Biophys J. 1993;65(2):955–963. - PMC - PubMed
    8. Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. The Fast Multipole Boundary-Element Method for Molecular Electrostatics - an Optimal Approach for Large Systems. J Comput Chem. 1995;16(7):898–913.
    9. Purisima EO, Nilar SH. A Simple yet Accurate Boundary-Element Method for Continuum Dielectric Calculations. J Comput Chem. 1995;16(6):681–689.
    10. Liang J, Subramaniam S. Computation of molecular electrostatics with boundary element methods. Biophys J. 1997;73(4):1830–1841. - PMC - PubMed
    11. Vorobjev YN, Scheraga HA. A fast adaptive multigrid boundary element method for macromolecular electrostatic computations in a solvent. J Comput Chem. 1997;18(4):569–583.
    12. Totrov M, Abagyan R. Rapid boundary element solvation electrostatics calculations in folding simulations: Successful folding of a 23-residue peptide. Biopolymers. 2001;60(2):124–133. - PubMed
    13. Boschitsch AH, Fenley MO, Zhou HX. Fast boundary element method for the linear Poisson-Boltzmann equation. J Phys Chem B. 2002;106(10):2741–2754.
    14. Lu BZ, Cheng XL, Huang JF, McCammon JA. Order N algorithm for computation of electrostatic interactions in biomolecular systems. Proc Natl Acad Sci U S A. 2006;103(51):19314–19319. - PMC - PubMed
    15. Lu B, Cheng X, Huang J, McCammon JA. An Adaptive Fast Multipole Boundary Element Method for Poisson-Boltzmann Electrostatics. J Chem Theory Comput. 2009;5(6):1692–1699. - PMC - PubMed
    16. Bajaj C, Chen SC, Rand A. An Efficient Higher-Order Fast Multipole Boundary Element Solution For Poisson-Boltzmann-Based Molecular Electrostatics. Siam Journal on Scientific Computing. 2011;33(2):826–848. - PMC - PubMed

LinkOut - more resources