Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2017 May 19;372(1720):20150520.
doi: 10.1098/rstb.2015.0520.

Vertex models: from cell mechanics to tissue morphogenesis

Silvanus Alt  1 , Poulami Ganguly  1 , Guillaume Salbreux  2
Affiliations
Review

Vertex models: from cell mechanics to tissue morphogenesis

Silvanus Alt et al. Philos Trans R Soc Lond B Biol Sci. .

Abstract

Tissue morphogenesis requires the collective, coordinated motion and deformation of a large number of cells. Vertex model simulations for tissue mechanics have been developed to bridge the scales between force generation at the cellular level and tissue deformation and flows. We review here various formulations of vertex models that have been proposed for describing tissues in two and three dimensions. We discuss a generic formulation using a virtual work differential, and we review applications of vertex models to biological morphogenetic processes. We also highlight recent efforts to obtain continuum theories of tissue mechanics, which are effective, coarse-grained descriptions of vertex models.This article is part of the themed issue 'Systems morphodynamics: understanding the development of tissue hardware'.

Keywords: epithelial mechanics; morphogenesis; simulations; tissue mechanics; vertex models.

PubMed Disclaimer

Figures

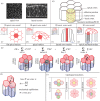
Figure 1.
Figure 1.
Properties of 2D and 3D vertex models for tissue mechanics. (a) Apical view (from [1]) and cross-section (from [2]) of the wing imaginal disc epithelium in the Drosophila embryo. (b) Schematic of an epithelial tissue. Cytoskeletal elements generate forces inside the cells, which are mechanically coupled to other cells and to the basement membrane. (c,d) In apical vertex models epithelial cells are represented by the shape of their apical surfaces, which are polygons either in 2D or in 3D. (e) In 2D lateral vertex models, cells are represented by their lateral cross-sections. (f) In 3D vertex models the tissue is represented by its apical and basal geometry. (g) A virtual work differential for vertex displacement, depending on changes in cell volume δVα, surface area δAk and edge length δlλ. External forces acting on vertices formula image can yield an additional contribution to the virtual work. (h) The force fv on a vertex v is obtained by taking the virtual work differential with respect to the vertex position xv. The tissue is in mechanical equilibrium when the force acting on all vertices is zero. (i) Topological transitions in epithelia are cell–cell intercalations (T1 transitions), cell extrusions (T2 transitions) and cell divisions.
Figure 2.
Figure 2.
Examples of biological processes described by vertex models. (a) 2D apical vertex models have been used to study cellular arrangements in planar epithelia. (top left) Cell packing topology in growing epithelia [,,–62]. The image shows a simulated epithelium where cells are coloured depending on their neighbour number (from [22]). (top right) Epithelial growth and size control [23,27,28,61,66]. The image shows the final shape of a growing epithelium with a morphogen concentration indicated in shades of green (from [23]). (bottom left) Interface smoothing between differently fated epithelia due to differential tension [25,30,67]. The image shows a simulation of the boundary between two compartments (red and blue) of the wing imaginal disc in Drosophila (from [25]). (bottom right) Simulation of cone photoreceptor packing in the zebrafish retina, showing ordering of cells due to polarized interfacial stresses (from [29]). (b) 3D apical vertex models for epithelia where the apical surfaces of cells move out of plane, and stresses are generated along the apical cell surfaces. (top left) Simulation of appendage formation on the Drosophila eggshell due to mechanical patterning (from [32]). (top right) Theoretical study of the buckling of a compressed epithelium (from [33]). (bottom left) Simulation showing epithelial folding due to apoptotic forces in the imaginal leg disc of Drosophila (from [34]). (bottom right) Simulation of anterior visceral endoderm migration (green) among the visceral endoderm (red) in the egg-cylinder stage mouse embryo (from [31]). (c) 2D lateral vertex models describe a cross-section of the epithelium. (top left) Simulation of neural tube formation in amphibians as a result of a ‘purse-string’ contraction of apical surfaces and cell volume conservation (from [35]). (top right) Phase diagram of epithelial buckling as a function of bending stiffness and differential tensions along the apical and basal surfaces of cells (from [40]). (bottom left) Simulation of ventral furrow formation in Drosophila (from [37]). (bottom right) Simulation of optical cup formation in mouse embryonic stem cell culture (from [36]). (d) 3D vertex models have been used to study deformations of epithelia in three dimensions taking into account stresses along apical, basal and lateral surfaces. (top left) Cyst formation in the Drosophila imaginal wing disc due to a contractile boundary; 3D geometry of the cells with an invaginating cyst in the centre (left) and a cross-section through the cyst (right) (from [2]). (top right) Deformations of a patterned spherical epithelia (from [44]). (bottom left) Simulation results of proliferating tissue with (left) and without (right) apical contractility, showing that apical and basal smoothness are increased with apical contractility (from [45]). (bottom right) Simulation of growth of epithelial vesicles, with different choices for viscous dissipation (from [43]).
Figure 3.
Figure 3.
Continuum approaches by coarse graining of vertex models. (a) In a continuum theory, the epithelium is represented by a 2D viscoelastic sheet [2,11,33,75]. (b) The shear modulus μ, the bulk modulus K and the bending modulus κ characterize the resistance to shear, isotropic stretching and bending of a thin elastic sheet in response to forces acting on the material. On timescales on which cellular neighbour exchange, cell division and cell delamination occur, in-plane isotropic and anisotropic stresses relax and the tissue exhibits a fluid behaviour.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Staple DB, Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. 2010. Mechanics and remodelling of cell packings in epithelia. Eur. Phys. J. E Soft Matter 33, 117–127. (10.1140/epje/i2010-10677-0) - DOI - PubMed
    1. Bielmeier C, Alt S, Weichselberger V, La Fortezza M, Harz H, Jülicher F, Salbreux G, Classen A-K. 2016. Interface contractility between differently fated cells drives cell elimination and cyst formation. Curr. Biol. 26, 563–574. (10.1016/j.cub.2015.12.063) - DOI - PMC - PubMed
    1. Howard J. 2001. Mechanics of motor proteins and the cytoskeleton. Sunderland, MA: Sinauer Associates.
    1. Heisenberg C-P, Bellaïche Y. 2013. Forces in tissue morphogenesis and patterning. Cell 153, 948–62. (10.1016/j.cell.2013.05.008) - DOI - PubMed
    1. Salbreux G, Charras G, Paluch E. 2012. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 22, 536–545. (10.1016/j.tcb.2012.07.001) - DOI - PubMed

LinkOut - more resources