Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 May 5;372(1719):20160084.
doi: 10.1098/rstb.2016.0084.

Breaking beta: deconstructing the parasite transmission function

Hamish McCallum  1 , Andy Fenton  2 , Peter J Hudson  3 , Brian Lee  4 , Beth Levick  2 , Rachel Norman  4 , Sarah E Perkins  5   6 , Mark Viney  7 , Anthony J Wilson  8 , Joanne Lello  9   6
Affiliations

Breaking beta: deconstructing the parasite transmission function

Hamish McCallum et al. Philos Trans R Soc Lond B Biol Sci. .

Abstract

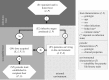
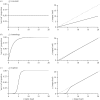
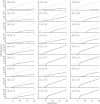
Transmission is a fundamental step in the life cycle of every parasite but it is also one of the most challenging processes to model and quantify. In most host-parasite models, the transmission process is encapsulated by a single parameter β Many different biological processes and interactions, acting on both hosts and infectious organisms, are subsumed in this single term. There are, however, at least two undesirable consequences of this high level of abstraction. First, nonlinearities and heterogeneities that can be critical to the dynamic behaviour of infections are poorly represented; second, estimating the transmission coefficient β from field data is often very difficult. In this paper, we present a conceptual model, which breaks the transmission process into its component parts. This deconstruction enables us to identify circumstances that generate nonlinearities in transmission, with potential implications for emergent transmission behaviour at individual and population scales. Such behaviour cannot be explained by the traditional linear transmission frameworks. The deconstruction also provides a clearer link to the empirical estimation of key components of transmission and enables the construction of flexible models that produce a unified understanding of the spread of both micro- and macro-parasite infectious disease agents.This article is part of the themed issue 'Opening the black box: re-examining the ecology and evolution of parasite transmission'.

Keywords: heterogeneity; infection; infectious disease; modelling; nonlinearities; transmission function.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Schematic decomposition of the transmission process. Hexagons represent parasite load in the donor (S1) and recipient (S5) hosts. Squares represent distinct stages of the transmission process and arrows represent transmission between stages. The letters I (infected host), P (parasite), E (environment) and S (susceptible host) represent potentially important factors acting at each stage relating to infectious (donor) host (I), the parasite, the environment and the susceptible (recipient) host (S), respectively.
Figure 2.
Figure 2.
Graphical representation of the functional forms used in the transmission stage, where the x-axis is the ‘input’ parasite load into each function (i.e. the load from the previous step in the pathway) for: (a) linear function, (b) saturating function and (c) logistic function. Left-hand column: the y-axis shows parasite ‘survival’ (proportion of parasite load completing that stage); right-hand column: absolute ‘output’ parasite load (y) completing that stage. The dotted lines show the 1 : 1 relationship. Parameter b = 0.5, c = 0.5, g = 2 and x0 = 5.
Figure 3.
Figure 3.
Overall transmission functions (relationship between initial infectious load in the donor host, L, and resultant infecting load in the recipient host, P) under all possible combinations of constant, saturating or logistic transmission functions, acting at each of the three stages in the transmission process described by equation (4.1). Each panel is marked with a label of the form {p, d, r}, which indicates the form of the transmission function (equations (4.3)–(4.5)) acting at the corresponding stage (p, d or r) of the overall transmission function in equation (4.1). The dotted lines show the 1 : 1 relationship. Parameter b = 0.5, c = 0.5, g = 2 and x0 = 5.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Lafferty KD, Deleo G, Briggs CJ, Dobson AP, Gross T, Kuris AM. 2015. A general consumer-resource population model. Science 349, 854–857. (10.1126/science.aaa6224) - DOI - PubMed
    1. Barlow ND. 2000. Non-linear transmission and simple models for bovine tuberculosis. J. Anim. Ecol. 69, 703–713. (10.1046/j.1365-2656.2000.00428.x) - DOI
    1. Anderson RM, Nokes DJ. 1991. Mathematical models of transmission and control. In Oxford textbook of public health (eds Holland WW, Detels R, Knox G), pp. 225–252. Oxford, UK: Oxford University Press.
    1. Begon M, Bennett M, Bowers RG, French NP, Hazel SM, Turner J. 2002. A clarification of transmission terms in host-microparasite models: numbers, densities and areas. Epidemiol. Infect. 129, 147–153. (10.1017/S0950268802007148) - DOI - PMC - PubMed
    1. Antolin MF. 2008. Unpacking beta: within-host dynamics and the evolutionary ecology of pathogen transmission. Annu. Rev. Ecol. Evol. Syst. 39, 415–437. (10.1146/annurev.ecolsys.37.091305.110119) - DOI