Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Apr 20;121(15):3747-3756.
doi: 10.1021/acs.jpcb.6b10732. Epub 2017 Mar 2.

Quantitative Characterization of Domain Motions in Molecular Machines

Suvrajit Maji  1 , Rezvan Shahoei  2   3   4 , Klaus Schulten  2   3   4 , Joachim Frank  1   5   6
Affiliations

Quantitative Characterization of Domain Motions in Molecular Machines

Suvrajit Maji et al. J Phys Chem B. .

Abstract

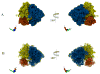
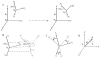
The work of molecular machines such as the ribosome is accompanied by conformational changes, often characterized by relative motions of their domains. The method we have developed seeks to quantify these motions in a general way, facilitating comparisons of results obtained by different researchers. Typically there are multiple snapshots of a structure in the form of pdb coordinates resulting from flexible fitting of low-resolution density maps, from X-ray crystallography, or from molecular dynamics simulation trajectories. Our objective is to characterize the motion of each domain as a coordinate transformation using moments of inertia tensor, a method we developed earlier. What has been missing until now are ancillary tools that make this task practical, general, and biologically informative. We have provided a comprehensive solution to this task with a set of tools implemented on the VMD platform. These tools address the need for reproducible segmentation of domains, and provide a generalized description of their motions using principal axes of inertia. Although this methodology has been specifically developed for studying ribosome motion, it is applicable to any molecular machine.

PubMed Disclaimer

Conflict of interest statement

Notes

The authors declare no competing financial interest.

Figures

Figure 1
Figure 1
Density Map Segmentation. A. Binary maps, generated by application of a threshold to the density map (central Z-axis slice shown); threshold = 0 (left) is appropriate while threshold = 0.5 (right) is unsuited for segmentation. B. Distance Transform (DT) of the complementary binary map ~Mbin (central Z-axis slice shown). C. Same map as in (B) but showing central X-axis slice (top) and Y-axis slice (bottom). D. Inverted distance transform map DT ≔ − DT. E. Same map as in (D) but showing central X-axis slice (top) and Y-axis slice (bottom). F. Distance Transform map with voxels corresponding to the background voxels of Mbin, labeled as −infinity, so that the background voxels becomes inaccessible. G. Same map as in (F) but showing central X-axis slice (top) and Y-axis slice (bottom). H. Segmentation of the volume maps after applying the Watershed Transform with region merging. I. Same map as in (F) but showing central X-axis slice (top) and Y-axis slice (bottom).
Figure 2
Figure 2
Segmentation of Ribosome Structure. A. Segmentation of the 3D density map of a ribosome structure into its three relevant domains: large subunit (LSU) (blue), small subunit (SSU) body (yellow), and SSU head (orange). B. Segmented atomic model of the ribosome. The segments were obtained by extracting the residues contained within the individual volume segments obtained from (A). VMD axes X(red), Y(green), Z(blue) are shown on the bottom left inset of each panel.
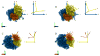
Figure 3
Figure 3
Principal axes computation for the segmented domains (Fig 2) of the ribosome structures in two states, “A” and “B”. The Principal axes for individual domains are shown with the same color as the corresponding domain. The inset on the right of each panel shows the Principal axes only. A. Principal axes of LSU (blue) and SSU body (yellow) for the structure in state “A”. B. Principal axes of LSU (blue) and SSU body (yellow) for the structure in state “B”. C. Principal axes of SSU body (yellow) and SSU head (orange) for the structure in state “A”. D. Principal axes of SSU body (yellow) and SSU head (orange) for the structure in state “B”. For panels (A) and (B), the LSU is fixed and aligned to the Cartesian VMD coordinate system axes XYZ. For panels (C) and (D), the SSU body is fixed and aligned to the Cartesian coordinate system axes XYZ.
Figure 4
Figure 4
Coordinate Axes Transformation using Absolute Orientation. A. Fixed reference frame denoted by the Principal axes of Inertia tensor RT. The domain moving relative to the fixed reference frame is denoted by the Principal axes of Inertia tensors DmT and DmT′ on the left hand side (lhs) and right hand side (rhs), respectively. The Principal axes P1, P2 & P3 (lhs) move to P1′, P2′ & P3′ (rhs), respectively. B. Schematic illustrating the Absolute Orientation problem for coordinate axes transformation between DmT and DmT′. There is a unique rotation and also a translation (given by the difference between the corresponding centers OD − OD′) to obtain the complete coordinate axes transformation. C. Special case where the origins for DmT & DmT′ coincide and the coordinate axes transformation is achieved just by rotating DmT by an angle θ about an axis perpendicular to the plane of rotation, to be transformed into DT′. D. Angle-axis representation for the unit quaternion q˚. The solution to the rotation for the coordinate axes transformation in B or C is given by q˚. The axis of rotation is given by ê and the angle of rotation is given by θ.
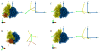
Figure 5
Figure 5
Characterization of domain motion between two structures “A” and “B” (Fig. 3) using the Absolute Orientation algorithm for the Principal Axes transformation from “A” to “B”. The resulting unit quaternion describing the rotation, is expressed in its axis-angle representation. The Principal axes for individual domains are shown with the same color as the corresponding domain, and the rotation axis is shown in green. The inset on the right of each panel shows the Principal axes and the rotation axis. A. Rotation of SSU body (yellow) from state “A” to “B”. The LSU remains fixed here. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B” B. Rotation of SSU head (orange) from state “A” to “B”. The SSU body remains fixed. The green arrow represents the axis of rotation of the SSU head between the states “A” and “B” and is drawn overlayed on model “B”. C. Rotation for the full SSU (yellow) from state “A” to “B”. The LSU remains fixed. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B”. D. Rotation of the full SSU (yellow) from state “A” to “B”. The LSU remains fixed here. The LSU and SSU, in this case, are obtained from a reference segmentation. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B”.
Figure 6
Figure 6
Characterizing the Error in Domain Segmentation and Domain Rotation. A. Segmentation quality measures, with Precision, Recall calculated for the full structure and F − measure calculated for the individual domains and also the full structure, in all the segmentation cases listed in Table S1. The plotted values are ranked based on the F-measure of the SSU (Table S4). B. Errors in rotation angle of the SSU for the segmentation cases and ranked in the same manner as in A.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Trabuco LG, Villa E, Schreiner E, Harrison CB, Schulten K. Molecular dynamics flexible fitting: a practical guide to combine cryo-electron microscopy and X-ray crystallography. Methods. 2009;49(2):174–80. - PMC - PubMed
    1. Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 2008;16(5):673–83. - PMC - PubMed
    1. Noel JK, Levi M, Raghunathan M, Lammert H, Hayes RL, Onuchic JN, Whitford PC. SMOG 2: A Versatile Software Package for Generating Structure-Based Models. PLoS computational biology. 2016;12(3):e1004794. - PMC - PubMed
    1. Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of molecular graphics. 1996;14(1):33–8. 27–8. - PubMed
    1. Behrmann E, Loerke J, Budkevich TV, Yamamoto K, Schmidt A, Penczek PA, Vos MR, Burger J, Mielke T, Scheerer P, Spahn CM. Structural snapshots of actively translating human ribosomes. Cell. 2015;161(4):845–57. - PMC - PubMed

Publication types

LinkOut - more resources