Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Feb;42(1):71-85.
doi: 10.1007/s10827-016-0628-2. Epub 2016 Oct 10.

Hierarchical winner-take-all particle swarm optimization social network for neural model fitting

Brandon S Coventry  1 , Aravindakshan Parthasarathy  1 , Alexandra L Sommer  1 , Edward L Bartlett  2
Affiliations

Hierarchical winner-take-all particle swarm optimization social network for neural model fitting

Brandon S Coventry et al. J Comput Neurosci. 2017 Feb.

Abstract

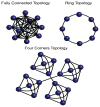
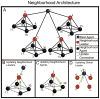
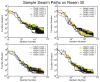
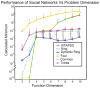
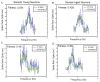
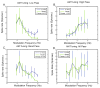
Particle swarm optimization (PSO) has gained widespread use as a general mathematical programming paradigm and seen use in a wide variety of optimization and machine learning problems. In this work, we introduce a new variant on the PSO social network and apply this method to the inverse problem of input parameter selection from recorded auditory neuron tuning curves. The topology of a PSO social network is a major contributor to optimization success. Here we propose a new social network which draws influence from winner-take-all coding found in visual cortical neurons. We show that the winner-take-all network performs exceptionally well on optimization problems with greater than 5 dimensions and runs at a lower iteration count as compared to other PSO topologies. Finally we show that this variant of PSO is able to recreate auditory frequency tuning curves and modulation transfer functions, making it a potentially useful tool for computational neuroscience models.

Keywords: Biological neural networks; Evolutionary computation; Model optimization; Particle swarm optimization.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
The continuum of social networks. Top left: The fully-connected topology is a fully-connected graph where each agent is directly connected to every other agent. Top right: The ring topology slows down information transfer by only allowing connections between an agents nearest neighbors. Bottom: Many social networks draw from aspects of both fully-connected and ring topologies. The four corners social network is fully-connected locally but sparsely connected between neighborhoods.
Fig. 2
Fig. 2
Hierarchical architecture for the winner-take-all particle swarm social network. A.) The overall topology of the WTAPSO social network. The global leader is shown as a blue sphere, while local neighborhood leaders and agents are shown as red and black spheres respectively. Numbers near agents represent a sample of agent placement in the swarm. By definition, the global leader is always 1, while local leaders represent the best performing agents of a given neighborhood. Once the best performing local agent is determined, update connections are broken, represented by dotted black lines, so that only good influences are updating the target agent. B.) A sample of updating a neighborhood leader. The neighborhoods are disconnected at update and only the best two performing agents are allowed to update the neighborhood leader. By its rank, the global leader always updates the neighborhood leader. C.) Updating a neighborhood agent is very similar to updating a neighborhood leader. Only the best two best performing agents are allowed to update the target agent. By virtue of its position, the local leader will always update the target agent, while the next best performing local agent acts as the other update agent. D.) The global leader receives update information from its own previous best performance and the best performing local leader.
Fig. 3
Fig. 3
Sample paths for WTAPSO on the Rosenbrock 30 problem. The global leader shows monotonically decreasing function values while the local leaders demonstrate decreasing trends with oscillations about error values, most likely due to the rearranging of the swarm networks. This also demonstrates WTAPSOs ability to move out of local minima until convergence at higher iteration values.
Fig. 4
Fig. 4
Social network performance versus dimensionality on the Rosenbrock function. While Canonical ring, dynamic ring, Common and Trelea social networks perform best in low dimensions, the winner take all social network performs on par with the toolbox Matlab toolbox Common network and better than all others. Significance was assessed by a two-way ANOVA with Tukey honestly-significant-difference post tests. * indicates a significant difference between WTAPSO and social network under test.
Fig. 5
Fig. 5
Recreation of in vivo FTCs using a biophysical neuron IC model using WTAPSO. Responses were illicited from sinusoid tones of varying frequencies. The fitness function varies between 0 and 1 with 1 being a better fit. Spontaneous responses were not fit, but set to rates typically seen in recordings (data not shown). WTAPSO is able to recreate a wide variety of responses types and shapes seen in vivo.
Fig. 6
Fig. 6
Example rMTFs. Functions were optimized around synaptic conductance values and input beta distribution priors. WTAPSO is able to recreate a wide variety of response classes including low-pass, high-pass, band-pass, and all-pass shapes.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Ackley DH. A Connectionist Machine for Genetic Hill-climbing. 1. Kluwer Academic Publishers; Boston: 1987.
    1. Bastian M, Heymann S, Jacomy M. Gephi: An Open Source Software for Exploring and Manipulating Networks. International AAAI Conference on Weblogs and Social Media. 2009:1–2.
    1. Birge B. Particle Swarm Optimization Toolbox. 2006.
    1. Blum C, Roli A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Computing Surveys. 2003 Sep;35(3):268–308.
    1. Carnevale NT, Hines ML. The NEURON Book. Vol. 30. Cambridge University Press; 2006.

LinkOut - more resources