Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Sep;204(1):77-87.
doi: 10.1534/genetics.116.190462. Epub 2016 Jul 13.

A Statistical Guide to the Design of Deep Mutational Scanning Experiments

Sebastian Matuszewski  1 , Marcel E Hildebrandt  2 , Ana-Hermina Ghenu  3 , Jeffrey D Jensen  4 , Claudia Bank  5
Affiliations

A Statistical Guide to the Design of Deep Mutational Scanning Experiments

Sebastian Matuszewski et al. Genetics. 2016 Sep.

Abstract

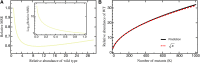
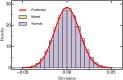
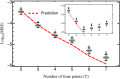
The characterization of the distribution of mutational effects is a key goal in evolutionary biology. Recently developed deep-sequencing approaches allow for accurate and simultaneous estimation of the fitness effects of hundreds of engineered mutations by monitoring their relative abundance across time points in a single bulk competition. Naturally, the achievable resolution of the estimated fitness effects depends on the specific experimental setup, the organism and type of mutations studied, and the sequencing technology utilized, among other factors. By means of analytical approximations and simulations, we provide guidelines for optimizing time-sampled deep-sequencing bulk competition experiments, focusing on the number of mutants, the sequencing depth, and the number of sampled time points. Our analytical results show that sampling more time points together with extending the duration of the experiment improves the achievable precision disproportionately compared with increasing the sequencing depth or reducing the number of competing mutants. Even if the duration of the experiment is fixed, sampling more time points and clustering these at the beginning and the end of the experiment increase experimental power and allow for efficient and precise assessment of the entire range of selection coefficients. Finally, we provide a formula for calculating the 95%-confidence interval for the measurement error estimate, which we implement as an interactive web tool. This allows for quantification of the maximum expected a priori precision of the experimental setup, as well as for a statistical threshold for determining deviations from neutrality for specific selection coefficient estimates.

Keywords: distribution of fitness effects; experimental design; experimental evolution; mutation; population genetics.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Comparison of the predicted mean squared error (Equation 10; red circles) and the average mean squared error (blue stars), obtained from 1000 simulated data sets for (A) different numbers of sampling time points T and mutants K, for sequencing depth D=100,000, and (B) different sequencing depth D, with fixed T=5, K=100. Boxes represent the interquartile range (i.e., the 50% C.I.), whiskers extend to the highest/lowest data point within the box ± 1.5 times the interquartile range, and black and gray circles represent close and far outliers, respectively. Results are presented on log scale.
Figure 2
Figure 2
(A) The relative MSE as a function of the relative abundance of the wild type, i.e., MSE(p1=x/K)/MSE(p1=1/K), for K=100. The inset shows results for p1≤1/K, where the y-axis has been put on log scale. The abundance of all other (except the wild type) is assumed to scale proportionally. (B) The relative wild-type abundance that minimizes the MSE as a function of the number of mutants K. An explicit formula (given by the black line) is not shown due to complexity, but can well be approximated by K. Either prediction is based on Equation 10. Other parameters: D=100,000.
Figure 3
Figure 3
Histogram of the deviation (Equation 6) between the estimated and true selection coefficients drawn from either a normal distribution or a mixture distribution (for details see Model and Methods) based on 1000 simulated data sets each. The red line is the prediction based on Equation 10. Other parameters: T=5, D=100,000, K=100.
Figure 4
Figure 4
Comparison of the predicted mean squared error (Equation 10; red) against the average mean squared error (blue stars) obtained from 1000 cross-validation data sets. Only mutants with an estimated selection coefficient larger than the intermediate between the estimated mean synonym and the estimated mean stop codon selection coefficient were considered. The inset shows the MSE calculated for all mutants. The MSE is presented on log scale. Other parameters: t=(4.8,7.2,9.6,12,16.8,26.4,36), DFigure=(474,931;636,257;873,827;1,513,392;424,182;443,739;452,326),DInset=(654,311;820,301;1,046,169;1,726,516;469,855;464,070;463,363), KFigure=400,KInset=568. Alternatively, in the presence of strongly deleterious mutants a Poisson regression may be used for estimating growth rates (see Figure S7).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bank C., Hietpas R. T., Wong A., Bolon D. N., Jensen J. D., 2014. A Bayesian MCMC approach to assess the complete distribution of fitness effects of new mutations: uncovering the potential for adaptive walks in challenging environments. Genetics 196: 841–852. - PMC - PubMed
    1. Bank C., Hietpas R. T., Jensen J. D., Bolon D. N., 2015. A systematic survey of an intragenic epistatic landscape. Mol. Biol. Evol. 32: 229–238. - PMC - PubMed
    1. Bataillon T., Bailey S. F., 2014. Effects of new mutations on fitness: insights from models and data. Ann. N. Y. Acad. Sci. 1320: 76–92. - PMC - PubMed
    1. Bernet G. P., Elena S. F., 2015. Distribution of mutational fitness effects and of epistasis in the 5′ untranslated region of a plant RNA virus. BMC Evol. Biol. 15: 1–13. - PMC - PubMed
    1. Boucher, J. I., D. N. A. Bolon, and D. S. Tawfik, 2016 Quantifying and understanding the fitness effects of protein mutations: Laboratory vs. nature. Protein Sci. 25(7): 1219–26. - PMC - PubMed

LinkOut - more resources