Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Jul 1;32(13):1943-51.
doi: 10.1093/bioinformatics/btw112. Epub 2016 Feb 26.

repgenHMM: a dynamic programming tool to infer the rules of immune receptor generation from sequence data

Yuval Elhanati  1 , Quentin Marcou  1 , Thierry Mora  2 , Aleksandra M Walczak  1
Affiliations

repgenHMM: a dynamic programming tool to infer the rules of immune receptor generation from sequence data

Yuval Elhanati et al. Bioinformatics. .

Abstract

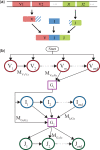
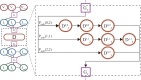
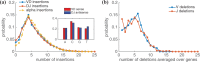
Motivation: The diversity of the immune repertoire is initially generated by random rearrangements of the receptor gene during early T and B cell development. Rearrangement scenarios are composed of random events-choices of gene templates, base pair deletions and insertions-described by probability distributions. Not all scenarios are equally likely, and the same receptor sequence may be obtained in several different ways. Quantifying the distribution of these rearrangements is an essential baseline for studying the immune system diversity. Inferring the properties of the distributions from receptor sequences is a computationally hard problem, requiring enumerating every possible scenario for every sampled receptor sequence.

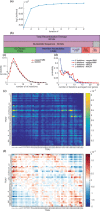
Results: We present a Hidden Markov model, which accounts for all plausible scenarios that can generate the receptor sequences. We developed and implemented a method based on the Baum-Welch algorithm that can efficiently infer the parameters for the different events of the rearrangement process. We tested our software tool on sequence data for both the alpha and beta chains of the T cell receptor. To test the validity of our algorithm, we also generated synthetic sequences produced by a known model, and confirmed that its parameters could be accurately inferred back from the sequences. The inferred model can be used to generate synthetic sequences, to calculate the probability of generation of any receptor sequence, as well as the theoretical diversity of the repertoire. We estimate this diversity to be [Formula: see text] for human T cells. The model gives a baseline to investigate the selection and dynamics of immune repertoires.

Availability and implementation: Source code and sample sequence files are available at https://bitbucket.org/yuvalel/repgenhmm/downloads

Contact: elhanati@lpt.ens.fr or tmora@lps.ens.fr or awalczak@lpt.ens.fr.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
(a) Schematic description of the rearrangement process for the alpha chains. Random V and J genes are chosen from the genome. A random number of nucleotides are trimmed from their facing ends. These ends are then joined with an insertion segment of variable length and composition. (b) Markov model for this rearrangement process, when the V and J gene choices are known. By progressing one path following the arrows, the model produces a rearranged receptor gene. Each state denoted by a circle emits a nucleotide. V and J states each emit one nucleotide from the chosen template, up to an error rate. Emissions from the I states are drawn from a specified distribution. The states represented by squares are nonemitting ghost states. The arrows represent the allowed transitions, some of them are marked on the diagram with MSS′. The probabilities of the transitions and emissions are the parameters of the HMM, as described in the main text
Fig. 2.
Fig. 2.
Subdiagram of Markov model for beta chain, focusing on the D gene. Each row corresponds to a different pattern of deletions (delDl,delDr) for the left and right ends of the D segments. State Dd(delDl,delDr) corresponds to the dth base in the D gene, when l bases are deleted from the left and r from the right. Each row is entered from the ghost state G2 with probability PdelD(l,r)=P(delDl,delDr), and then proceeds deterministically until G3.
Fig. 3.
Fig. 3.
TCR alpha chain rearrangement distribution inferred from sequence data taken from Zvyagin et al. (2014). (a) The log-likelihood of the data given the model saturates as a function of the number of iterations of the Expectation–Maximization algorithm. (b) Shannon entropy of rearrangements (top row) and sequences (middle row). The sequence entropy is lower than the total recombination entropy because of convergent rearrangements. The rearrangement entropy is the sum of entropies of its elementary events (bottom row). (c) Distribution of the number of inserted nucleotides (solid curve). For comparison, the same distribution obtained by the MiXCR software is represented by a dashed line. (d) Distributions of the number of deletions for both V and J genes, averaged over genes. (e) Joint distribution for V and J usage, P(V, J). Genes are ordered by position along the genome. (f) The covariance P(V,J)−P(V)P(J) clearly shows strong correlations for genes that are either close to the separation between the V and J segments, or far from it
Fig. 4.
Fig. 4.
Performance of the algorithm on synthetic data. Sequences generated using a known model were given as an input to the inference algorithm. The results of the inference are compared to the true model used for generation, for (a) the distribution of the number of insertions (inset: usage of inserted nucleotides) and (b) V, J gene usage. The error bars, which correspond to sample noise, are smaller than symbol size for (a). In (a) we also report the distribution of insertions obtained using MiXCR
Fig. 5.
Fig. 5.
TCR beta chain rearrangement distribution inferred from sequence data previously analyzed in (Murugan et al., 2012). (a) Distribution of the number of insertions at both VD and DJ junctions, and comparison with the distribution of insertion in the alpha chain from Figure 3c. Inset: The nucleotide usage is identical for VD and DJ insertions when considered on opposite strands. (b) Distribution of the number of deletions on both the V and J genes, averaged over different genes
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bishop C.M. (2006). Pattern Recognition and Machine Learning. New York, USA: Springer.
    1. Bolotin D.A. et al. (2012) Next generation sequencing for TCR repertoire profiling: platform-specific features and correction algorithms. Eur. J. Immunol., 42, 3073–3083. - PubMed
    1. Bolotin D.A. et al. (2015) MiXCR: software for comprehensive adaptive immunity profiling. Nat. Methods, 12, 380–381. - PubMed
    1. Bonissone S, Pevzner P. (2015). Immunoglobulin classification using the colored antibody graph In: Przytycka T.M. (ed.) Research in Computational Molecular Biology SE - 7, volume 9029 of Lecture Notes in Computer Science. Switzerland: Springer International Publishing, pp. 44–59.
    1. Brochet X. et al. (2008) IMGT/V-QUEST: the highly customized and integrated system for IG and TR standardized V-J and V-D-J sequence analysis. Nucleic Acids Res., 36, 503–508. - PMC - PubMed

Substances