Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Apr;202(4):1313-28.
doi: 10.1534/genetics.115.183905. Epub 2016 Feb 11.

Estimating Modifying Effect of Age on Genetic and Environmental Variance Components in Twin Models

Liang He  1 , Mikko J Sillanpää  2 , Karri Silventoinen  3 , Jaakko Kaprio  4 , Janne Pitkäniemi  5
Affiliations

Estimating Modifying Effect of Age on Genetic and Environmental Variance Components in Twin Models

Liang He et al. Genetics. 2016 Apr.

Abstract

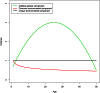
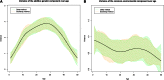
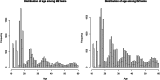
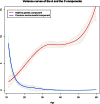
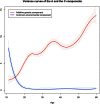
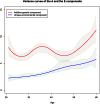
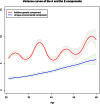
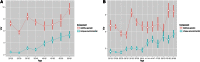
Twin studies have been adopted for decades to disentangle the relative genetic and environmental contributions for a wide range of traits. However, heritability estimation based on the classical twin models does not take into account dynamic behavior of the variance components over age. Varying variance of the genetic component over age can imply the existence of gene-environment (G×E) interactions that general genome-wide association studies (GWAS) fail to capture, which may lead to the inconsistency of heritability estimates between twin design and GWAS. Existing parametricG×Einteraction models for twin studies are limited by assuming a linear or quadratic form of the variance curves with respect to a moderator that can, however, be overly restricted in reality. Here we propose spline-based approaches to explore the variance curves of the genetic and environmental components. We choose the additive genetic, common, and unique environmental variance components (ACE) model as the starting point. We treat the component variances as variance functions with respect to age modeled by B-splines or P-splines. We develop an empirical Bayes method to estimate the variance curves together with their confidence bands and provide an R package for public use. Our simulations demonstrate that the proposed methods accurately capture dynamic behavior of the component variances in terms of mean square errors with a data set of >10,000 twin pairs. Using the proposed methods as an alternative and major extension to the classical twin models, our analyses with a large-scale Finnish twin data set (19,510 MZ twins and 27,312 DZ same-sex twins) discover that the variances of the A, C, and E components for body mass index (BMI) change substantially across life span in different patterns and the heritability of BMI drops to ∼50% after middle age. The results further indicate that the decline of heritability is due to increasing unique environmental variance, which provides more insights into age-specific heritability of BMI and evidence ofG×Einteractions. These findings highlight the fundamental importance and implication of the proposed models in facilitating twin studies to investigate the heritability specific to age and other modifying factors.

Keywords: age-specific heritability; body mass index; empirical Bayes predictor; penalized B-splines; twin models.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Variance functions of the A, C, and E components investigated in the simulation study.
Figure 2
Figure 2
Confidence bands constructed from the Delta and bootstrap methods for the A (shown in A) and C (shown in B) components.
Figure 3
Figure 3
Distributions of age among MZ and DZ twins.
Figure 4
Figure 4
The variance curves of the A and C components with the 95% confidence bands estimated from the ACE(t) model.
Figure 5
Figure 5
The variance curves of the A and C components with the 95% confidence bands estimated from the ACE(t)-p model.
Figure 6
Figure 6
The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the AE(t) model.
Figure 7
Figure 7
The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the AE(t)-p model.
Figure 8
Figure 8
The variance curves after age 20 years of the A and E components with the 95% confidence bands estimated from the stratified analyses. (A) Divided by 5-year intervals. (B) Divided by 3-year intervals.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Akaike H., 1969. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 21: 243–247.
    1. Atchley W. R., Rutledge J. J., 1980. Genetic components of size and shape. I. Dynamics of components of phenotypic variability and covariability during ontogeny in the laboratory rat. Evolution 34: 1161–1173. - PubMed
    1. Boker S., Neale M., Maes H., Wilde M., Spiegel M. et al, 2011. OpenMx: an open source extended structural equation modeling framework. Psychometrika 76: 306–317. - PMC - PubMed
    1. Boomsma D. I., Martin N. G., Molenaar P. C., 1989. Factor and simplex models for repeated measures: application to two psychomotor measures of alcohol sensitivity in twins. Behav. Genet. 19: 79–96. - PubMed
    1. Booth J. G., Hobert J. P., 1998. Standard errors of prediction in generalized linear mixed models. J. Am. Stat. Assoc. 93: 262–272.

Publication types