Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Jul 7;109(1):135-43.
doi: 10.1016/j.bpj.2015.06.005.

Thermodynamics of long supercoiled molecules: insights from highly efficient Monte Carlo simulations

Thibaut Lepage  1 , François Képès  2 , Ivan Junier  3
Affiliations

Thermodynamics of long supercoiled molecules: insights from highly efficient Monte Carlo simulations

Thibaut Lepage et al. Biophys J. .

Abstract

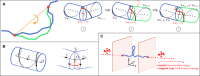
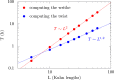
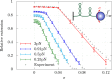
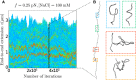
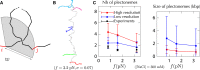
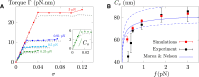
Supercoiled DNA polymer models for which the torsional energy depends on the total twist of molecules (Tw) are a priori well suited for thermodynamic analysis of long molecules. So far, nevertheless, the exact determination of Tw in these models has been based on a computation of the writhe of the molecules (Wr) by exploiting the conservation of the linking number, Lk=Tw+Wr, which reflects topological constraints coming from the helical nature of DNA. Because Wr is equal to the number of times the main axis of a DNA molecule winds around itself, current Monte Carlo algorithms have a quadratic time complexity, O(L(2)), with respect to the contour length (L) of the molecules. Here, we present an efficient method to compute Tw exactly, leading in principle to algorithms with a linear complexity, which in practice is O(L(1.2)). Specifically, we use a discrete wormlike chain that includes the explicit double-helix structure of DNA and where the linking number is conserved by continuously preventing the generation of twist between any two consecutive cylinders of the discretized chain. As an application, we show that long (up to 21 kbp) linear molecules stretched by mechanical forces akin to magnetic tweezers contain, in the buckling regime, multiple and branched plectonemes that often coexist with curls and helices, and whose length and number are in good agreement with experiments. By attaching the ends of the molecules to a reservoir of twists with which these can exchange helix turns, we also show how to compute the torques in these models. As an example, we report values that are in good agreement with experiments and that concern the longest molecules that have been studied so far (16 kbp).

PubMed Disclaimer

Figures

Figure 1
Figure 1
Torsionally induced super-structuring of DNA molecules. (Left) In vivo, plectonemes, which can be branched, occur because, e.g., of the activity of RNA polymerases and of the anchoring of DNA to the membrane (52). (Right) Topological constraints are exerted in vitro by keeping one end of a molecule fixed and adding helix turns at the other end, thanks to magnetic tweezers (9). To see this figure in color, go online.
Figure 2
Figure 2
A local MC algorithm for simulating supercoiled molecules. (A) (Left) In the discrete version of the sWLC, a rotation of a block of cylinders (green) changes the relative direction of the pairs of cylinders that are on each side of the pivots (red). (Right) (1) In our algorithm, every cylinder, i, is allocated with a twist, Twi, that is equal to the helicoidal winding of the strands (one strand is indicated in black). Schematically, pivots correspond to infinitesimal segments (red s) that connect the main axis of the pivot cylinders (dashed lines). Strand continuity between contiguous cylinders is then ensured by using a junction segment (red S) that is kept parallel with s such that S does not contribute to the overall twist (TwS=0) (see B for further details). (2) A rotation misaligns S with respect to s, generating some twist, TwS≠0. (3) As indicated by the red arrows, TwS=0 is recovered by displacing the end and start positions of the strands around the pivot such that S remains parallel to s, which results in a variation of the length of the strands in each pivot cylinder. The corresponding twist variations within each cylinder and, hence, the corresponding variation of the writhe can thus be easily computed, leading to an algorithm with a theoretical linear time complexity (see main text). (B) In practice, a junction strand, S, corresponds to a piece of strand that connects the end and start points (black points) of the strands associated to two consecutive cylinders—to this end, we use additional coordinates to mark the entry and exit points of the helix of every cylinder. The junction strand is constrained to remain within a plane that is parallel to the plane defined by the main axis of the two cylinders, t→i and t→i+1. To this end, the start point of the strand in i+1 is obtained by rotation of the end point in i around the axis (O,n→), with O the intersection of the main axis and n→=t→i∧t→i+1. Junction strands, although ensuring the continuity of the molecule, do not thus generate any twist, because they remain parallel to the main axis of the molecule. (C) For linear open chains (blue), the conservation of the linking number is implemented by closing the chain at infinity. To this end, we consider at each end of the molecule an infinitely long cylinder (dashed red lines). These external cylinders cannot rotate; they can only translate, as indicated by the red arrows, to follow the motion of the end pivots (red spheres). As originally discussed by Vologodskii and Marko (17), this framework makes it possible to properly handle the conservation of the linking number by associating the well-defined linking number of the closed, infinitely long chain to that of the open chain, which is otherwise ill-defined. To ensure the conservation of this linking number, we further prevent the open chain from crossing the virtual cylinders. In practice, we prevent the open chain from going beyond the end points along the z-axis, as indicated here by the two red walls (the same hard-wall boundary condition was implemented as well in Vologodskii and Marko (17)). Very interestingly, the use of external cylinders further opens the possibility to compute, in a direct way, the torques that are exerted by the open chain. To this end, a torsional energy, characterized by a torsional stiffness, is associated to the excess twist that is transferred from the end cylinders of the open chain to the external cylinders. By losing their torsional neutrality, external cylinders thus behave as magnetic traps, which can be used to investigate the torsional response of the open chain (see Torque measurements for further details). To see this figure in color, go online.
Figure 3
Figure 3
Algorithm performances. Time T in hours (h) needed to perform 107 block rotations, as a function of the length, L, of the chain, measured in Kuhn lengths (lKuhn=2lp). Blue dots indicate our algorithm, which consists of computing the twist. Red dots represent the classical algorithm (25), consisting of computing the writhe. Straight lines are the best fits to a power law. To see this figure in color, go online.
Figure 4
Figure 4
Simulating long supercoiled molecules. Relative extension of a simulated 16 kbp DNA molecule (533 cylinders) as a function of σ for different stretching forces, with C=86 nm, lp=50 nm, and re=2 nm ([NaCl]=100mM). Bars indicate the mean ± SD over four simulations of 107 iterations. Black crosses represent experimental results (11), where one end of the molecule is kept fixed and the other end is manipulated by magnetic tweezers (upper right), allowing to add helix turns to the molecule and to stretch it. To see this figure in color, go online
Figure 5
Figure 5
Structural insights of long supercoiled molecules in the buckling regime. (A) Plectoneme tracking in a 21 kbp molecule using a color code that reflects the density of DNA on the axis along which the molecule is stretched (see the Supporting Material for details) (inspired by the work of van Loenhout and colleagues (16)). High densities (red) reveal plectonemic structures that can be more or less branched, as shown by extracting a particular conformation—the red and orange zooms indicate a branched and a straight plectoneme, respectively. (B) Plectonemes can coexist with curls (blue zoom) and helices (green zoom). To see this figure in color, go online.
Figure 6
Figure 6
Plectoneme properties in the buckling regime. (A) In the spirit of the van Loenhout study (16), we developed a method to detect, count, and measure the plectonemes obtained in our simulations. Namely, for each cylinder i, we test whether i is the starting point of a plectoneme, that is, if there exist cylinders much farther away along the chain that are in the neighborhood of i. Denoting w as the expected width of plectonemes, we thus search whether there exists a cylinder at least 500 bp away from i that is located within a distance w of i (500 bp is the resolution reported by van Loenhout and colleagues (16)). If so, we consider as the end of the plectoneme (j in the figure) the cylinder with this property that is the most distant from i along the DNA. We then repeat the procedure from cylinder j+1, and so on. Here, we report results using an expected width w=2K/f (2), which lies between 16 and 32 nm in the experiments presented here—the exact value of w actually has a negligible effect (Fig. S7). (B) Application of the method on a 21 kbp molecule (1400 cylinders) using f=3.2 pN and σ=0.07, where five plectonemes are detected and painted with different colors (note that the blue ones are branched). (C) Using this automatic detection, compared to the results of van Loenhout and colleagues (16) (black), we obtain a significantly higher number of plectonemes (red). To be able to properly compare our results with experiments, we further consider the spatial resolution (∼500 nm (16)) that is intrinsic to the fluorescent staining of DNA due to light diffraction. To this end, we merge the plectonemes whenever their distance along z is <500 nm. In this case, we still find a larger number of plectonemes (blue) but that is nevertheless consistent with experimental results. Here, parameters of the simulations are such that 25% of DNA is plectonemic (16). The bars indicate the standard variation over 12 simulations. To see this figure in color, go online.
Figure 7
Figure 7
(A) Direct numerical estimation of the torque, Γ, for different f and σ for a 16 kbp molecule. (Inset) At low forces ( f=0.25 pN), our estimation of Cs, which is proportional to the slope of Γ(σ) (44), is consistent with the experimental torques of Mosconi et al. (11). Discrepancies in (B) between experiments and simulations for the estimation of Cs at f<0.5 pN are thus likely to be due to a too small number of experimental points. (B) The effective torsional modulus, Cs, as a function of f. Simulations were run using C=86 nm. The solid blue line represents the large force expansion by Moroz and Nelson (44) using C=86 nm. Dashed blue lines show the same expansions but using C=80 nm (lower curve) and C=100 nm (upper curve), hence justifying the use of C=86 nm. The bars indicate the mean ± SE. To see this figure in color, go online.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Vologodskii A.V., Cozzarelli N.R. Conformational and thermodynamic properties of supercoiled DNA. Annu. Rev. Biophys. Biomol. Struct. 1994;23:609–643. - PubMed
    1. Strick T.R., Dessinges M.-N., Croquette V. Stretching of macromolecules and proteins. Rep. Prog. Phys. 2003;66:1–46.
    1. Travers A., Muskhelishvili G. DNA supercoiling—a global transcriptional regulator for enterobacterial growth? Nat. Rev. Microbiol. 2005;3:157–169. - PubMed
    1. Benza V.G., Bassetti B., Lagomarsino M.C. Physical descriptions of the bacterial nucleoid at large scales, and their biological implications. Rep. Prog. Phys. 2012;75:076602. - PubMed
    1. Junier I. Conserved patterns in bacterial genomes: a conundrum physically tailored by evolutionary tinkering. Comput. Biol. Chem. 2014;53 Pt A:125–133. - PubMed

Publication types

Substances