Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Sep 3;43(15):e97.
doi: 10.1093/nar/gkv412. Epub 2015 Apr 29.

Why weight? Modelling sample and observational level variability improves power in RNA-seq analyses

Ruijie Liu  1 , Aliaksei Z Holik  2 , Shian Su  1 , Natasha Jansz  3 , Kelan Chen  3 , Huei San Leong  3 , Marnie E Blewitt  3 , Marie-Liesse Asselin-Labat  2 , Gordon K Smyth  4 , Matthew E Ritchie  5
Affiliations

Why weight? Modelling sample and observational level variability improves power in RNA-seq analyses

Ruijie Liu et al. Nucleic Acids Res. .

Abstract

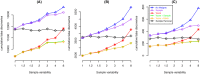
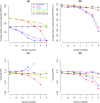
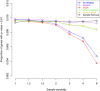
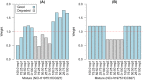
Variations in sample quality are frequently encountered in small RNA-sequencing experiments, and pose a major challenge in a differential expression analysis. Removal of high variation samples reduces noise, but at a cost of reducing power, thus limiting our ability to detect biologically meaningful changes. Similarly, retaining these samples in the analysis may not reveal any statistically significant changes due to the higher noise level. A compromise is to use all available data, but to down-weight the observations from more variable samples. We describe a statistical approach that facilitates this by modelling heterogeneity at both the sample and observational levels as part of the differential expression analysis. At the sample level this is achieved by fitting a log-linear variance model that includes common sample-specific or group-specific parameters that are shared between genes. The estimated sample variance factors are then converted to weights and combined with observational level weights obtained from the mean-variance relationship of the log-counts-per-million using 'voom'. A comprehensive analysis involving both simulations and experimental RNA-sequencing data demonstrates that this strategy leads to a universally more powerful analysis and fewer false discoveries when compared to conventional approaches. This methodology has wide application and is implemented in the open-source 'limma' package.

PubMed Disclaimer

Figures

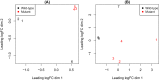
Figure 1.
Figure 1.
RNA-seq data sets where variations in sample quality are evident. Each panel shows a multi-dimensional scaling (MDS) plot, with samples colour-coded by experimental group. One or more samples that exhibit higher variability than average are present in each case ((A): sample 6; (B): samples 1 and 7). In these experiments, cells carrying a mutant allele of the gene Smchd1 were compared against wild-type cells.
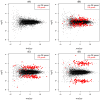
Figure 2.
Figure 2.
Log2(FC) versus average log2(expression level) for simulated data with 10 000 genes for samples with equivalent variability. (A) Null simulation with no differential expression (FC = 0 for all genes). (B) 200 DE genes with |FC| = 1.5. (C) 200 DE genes with |FC| = 2. (D) 200 DE genes with |FC| = 4.
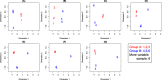
Figure 3.
Figure 3.
MDS plots from simulated data for different variability settings for sample 6 ranging from equivalent variability (A) to 120% (B), 150% (C), 200% (D), 300% (E), 400% (F) and 800% (G) more variability than the first five samples. Results shown are from a typical simulation of 10 000 genes, 200 of which have a |FC| = 4 (highlighted in red in Figure 2D).
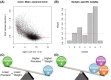
Figure 4.
Figure 4.
Weighting strategy where ‘voom’ weights (A) that model the mean-variance trend in the data and down-weight low-intensity observations are combined with sample-specific weights (B) or similar to model variability between different samples. Our default strategy is to model variability separately for each sample (C) so that each observation from a particular sample shares a common sample variance factor, which is converted into a weight (B). A second option allows samples to be grouped together (D) in a user-defined manner by specifying a design matrix for the variance model. We refer to this as our ‘block’ model.
Figure 5.
Figure 5.
Cumulative false discoveries across 100 simulated data sets for a two-group simulation with n = 3 samples per group. Each panel shows results from simulations with different true positive FCs: 1.5-fold (A), 2-fold (B) and 4-fold (C). The y-axis shows the cumulative number of false positives amongst the top 200 genes from each analysis method across 100 independent simulations of each setting. The x-axis indicates the simulated sample variability of the sixth sample. The results from these 21 simulation settings are representative of the 511 settings explored (see ‘Supplementary Materials’ for the complete results).
Figure 6.
Figure 6.
Plot assessing power (A,B) and the corresponding empirical FDR (C, D) at an FDR cut-off of 0.1 averaged across 100 simulated data sets. Results shown are for simulations where the TPs have |FC| = 2 (A, C) and |FC| = 4 (B, D) for various variabilities for the sixth sample (x-axis) for a two-group simulation with n = 3 samples per group. In panel (C), the empirical FDR values for sample weighting only that are off the scale are 0.42 for 400% and 0.68 for 800%. For the other methods (no weighting and ‘voom’ only), points were omitted in panel (C) when the average number of discoveries (panel (A)) was less than one gene to avoid ratios of small numbers that produce very variable FDRs. In most panels, results from combining either ‘voom’ and sample weights or ‘voom’ and block weights are over plotted as the results are the same. Boxplots of the results for each analysis method across the 100 simulated data sets generated under each sample variability setting are provided as ‘Supplementary Materials’.
Figure 7.
Figure 7.
Average type I error rates from null simulations (FC = 1 for all genes) using a P-value cut-off of 0.01 from 100 data sets with n = 3 samples per group. All methods control the false discovery rate at this level, irrespective of the simulated variability of the sixth sample (x-axis). ‘Voom’ on the full data set (red line) and not using weights (blue line) becomes increasingly conservative as sample variability increases.
Figure 8.
Figure 8.
Degraded RNA samples (replicate 2, shaded in grey) from the control experiment are correctly assigned lower weights by the combined ‘voom’ and sample weighting procedure (A), with an average weight of 0.70 across these five samples, compared to an average of 1.28 for the non-degraded samples (replicates 1 and 3, shaded in blue). A similar result is obtained for block weighting (B), with a weight of 0.71 assigned to the five degraded samples versus 1.20 for the remaining samples. When ‘voom’ was combined with sample weighting on the good samples, the weights were equivalent for the replicate 2 samples (1.06) and the remaining samples (1.07, data not shown).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Oshlack A., Robinson M.D., Young M.D. From RNA-seq reads to differential expression results. Genome Biol. 2010;11:220. - PMC - PubMed
    1. Hansen K.D., Brenner S.E., Dudoit S. Biases in Illumina transcriptome sequencing caused by random hexamer priming. Nucleic Acids Res. 2010;38:e131. - PMC - PubMed
    1. Robinson M.D., Oshlack A. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010;11:R25. - PMC - PubMed
    1. Risso D., Ngai J., Speed T.P., Dudoit S. Normalization of RNA-seq data using factor analysis of control genes or samples. Nat. Biotechnol. 2014;32:896–902. - PMC - PubMed
    1. Leek J.T. svaseq: removing batch effects and other unwanted noise from sequencing data. Nucleic Acids Res. 2014 doi:10.1093/nar/gku864. - PMC - PubMed

Publication types

Substances