Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Dec 18:590:1-15.
doi: 10.1016/j.cplett.2013.10.075.

Radical re-appraisal of water structure in hydrophilic confinement

Alan K Soper  1
Affiliations

Radical re-appraisal of water structure in hydrophilic confinement

Alan K Soper. Chem Phys Lett. .

Abstract

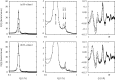
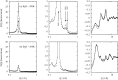
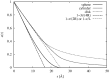
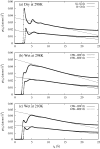
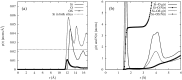
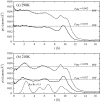
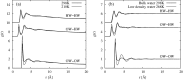
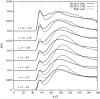
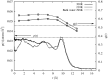
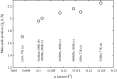
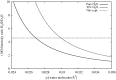
The structure of water confined in MCM41 silica cylindrical pores is studied to determine whether confined water is simply a version of the bulk liquid which can be substantially supercooled without crystallisation. A combination of total neutron scattering from the porous silica, both wet and dry, and computer simulation using a realistic model of the scattering substrate is used. The water in the pore is divided into three regions: core, interfacial and overlap. The average local densities of water in these simulations are found to be about 20% lower than bulk water density, while the density in the core region is below, but closer to, the bulk density. There is a decrease in both local and core densities when the temperature is lowered from 298 K to 210 K. The radical proposal is made here that water in hydrophilic confinement is under significant tension, around -100 MPa, inside the pore.

PubMed Disclaimer

Figures

None
Graphical abstract
Fig. 1
Fig. 1
Computer simulation box of dry MCM41, along the c-axis (a) and at right angles to the c-axis (along the a-axis (b). The dimensions of the box are 66.2Å along each of the a and b axes, and 148Å along the c axis. The small red dots at the centre of each pore represent the Q-atoms mentioned in the text: these make no contribution to the scattering pattern, but are used simply to prevent silica and “silanol” water molecules from entering the pores. Silanol water molecules populate the surface of the pores, but some of these are seen to permeate the silica matrix as well.
Fig. 2
Fig. 2
EPSR fit (line) to the total scattering data from dry MCM41 (circles) over three different scales of intensity and Q. Row (a) shows the fits to the data with protiated silanol water molecules, while row (b) shows the fit to the data with deuteriated silanol water molecules.The left-hand plot shows the (1 0 0) Bragg peak, the middle plot shows the (110), (200) and higher order Bragg peaks, while the right-hand plot shows the wider Q region beyond Q = 1Å−1.
Fig. 3
Fig. 3
EPSR fit (line) to the total scattering data from wet MCM41 at 298 K (circles) over three different scales of intensity and Q. Row (a) shows the fits to the data with absorbed H2O water molecules, while row (b) shows the fit to the data with D2O water molecules.The left-hand plot shows the (1 0 0) Bragg peak, the middle plot shows the (1 1 0), (2 0 0) and higher order Bragg peaks, while the right-hand plot shows the wider Q region beyond Q = 1Å−1.
Fig. 4
Fig. 4
EPSR fit (line) to the total scattering data from wet MCM41 at 210 K (circles) over three different scales of intensity and Q. Row (a) shows the fits to the data with absorbed H2O water molecules, while row (b) shows the fit to the data with D2O water molecules.The left-hand plot shows the (1 0 0) Bragg peak, the middle plot shows the (1 1 0), (2 0 0) and higher order Bragg peaks, while the right-hand plot shows the wider Q region beyond Q = 1Å−1.
Fig. 7
Fig. 7
Autocorrelation function, c(r) for a sphere of radius R = 12.5 Å (solid), infinitely long cylinder of radius R = 12.5 Å (dashed), and infinitely wide disk of thickness L = 25 Å (dotted). Also shown are the lines corresponding to the sphere at low r (dot–dashed) and the cylinder or disk at low r (intermittent dots).
Fig. 8
Fig. 8
Local density calculations (Eq. (9), middle expression) for the Si–Si and O–O radial distribution functions in dry MCM41 (a), and for the OW–OW and HW–HW radial distribution functions in wet MCM41 at 298 K (b) and 210 K (c). The straight lines defined by Eq. (9), right-hand expression, were fit in the region 5–15 Å. Parameters from these fits are given in Table 2. For O–O and HW–HW it was assumed the local density was twice the Si and OW local densities respectively, and the confining dimensions for O and HW were assumed to be the same as for Si and OW respectively.
Fig. 5
Fig. 5
(a) Density profile of Si (solid), O (dashed) and OS (dashed, crosses) of the simulated dry MCM41 substrate. Also shown is the expected bulk density of Si atoms (dotted). (b) Si–O (solid) and Si–OS (dashed) radial distribution functions, together with the corresponding running coordination numbers, NSiO(r) (solid, circles) and NSiOS(r) (dashed, crosses).
Fig. 9
Fig. 9
Water density profiles for OW (solid) and HW (dashed) atoms as a function of distance from the centre of the pore, at 298 K (a) and 210 K (b). Also shown (dotted) is a horizontal line corresponding to the average density in the range r = 0–4 Å at each temperature. This density is called the “core” density. The dot–dash line shows a simulation of ice Ih with the ice c-axis aligned with the cylindrical pore axis and the centre of hexagon at the centre of the pore.
Fig. 10
Fig. 10
Plots of the EPSR simulation of water in MCM41 for one of cylindrical pores at 298 K (a) and 210 K (b). There is little sign of obvious density fluctuations along the pore at either temperature.
Fig. 6
Fig. 6
(a) OW–OW, OW–HW and HW–HW radial distribution functions for water absorbed in MCM41 at 298 K (solid) and at 210 K (dashed). (b) Same functions for bulk water (solid) . Also shown are the estimated radial distribution functions for low density water at 268 K (dashed), as derived in . In both cases the OW–HW and HW–HW are shifted vertically for clarity.
Fig. 11
Fig. 11
OW–OW–OW included angle distribution, P(θ), for the specified distance ranges from the centre of the pore at 298 K (solid) and 210 K (dashed). To define each neighbour of the triangle the maximum OW–OW distance was set 3.24 Å. The dotted line shows the same distribution for bulk water at 298 K, determined from EPSR simulation of the merged diffraction data presented in with the same reference potential as used here.
Fig. 12
Fig. 12
Variation of absorbed water density as a function of distance from the centre of the MCM41 cylindrical pore (bottom plots, left-hand scale). Variation of q over the same distance range (top, right-hand scale). The results at 298 K are shown as the solid lines, and those at 210 K by the dashed lines. The dotted lines show the respective values for bulk water.
Fig. 13
Fig. 13
Position of the main peak in the diffraction pattern for water and amorphous ice (D2O) as a function atomic number density. The data are taken from (a) , (b) , (c) and (d) .
Fig. 14
Fig. 14
Predicted (1 0 0) Bragg peak intensity ratio (solid), H2O/D2O, Eq. (12) as a function of water density inside the pore, assuming a uniform density profile and sharp edges at the pore wall. The density of the silica is taken to be that of bulk silica. Also shown is the case where the D2O is contaminated with 10 mol% H2O (dashed). The dotted line shows the ratio found in the current experiment.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Poole P.H., Sciortino F., Essmann U., Stanley H.E. Nature. 1992;360:324.
    1. Stanley H., Angell C., Essmann U., Hemmati M., Poole P., Sciortino F. Phys. A Statist. Mech. Appl. 1994;205:122.
    1. Harrington S., Zhang R., Poole P.H., Sciortino F., Stanley H.E. Phys. Rev. Lett. 1997;78:2409.
    1. Brovchenko I., Geiger A., Oleinikova A. J. Chem. Phys. 2005;123:044515. - PubMed
    1. Liu Y., Panagiotopoulos A.Z., Debenedetti P.G. J. Chem. Phys. 2009;131:104508.

LinkOut - more resources