A numerical study on the dynamics of droplet formation in a microfluidic double T-junction
- PMID: 25825622
- PMCID: PMC4376751
- DOI: 10.1063/1.4916228
A numerical study on the dynamics of droplet formation in a microfluidic double T-junction
Abstract
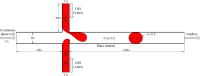
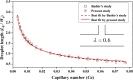
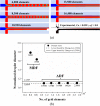
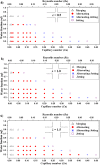
In this study, droplet formations in microfluidic double T-junctions (MFDTD) are investigated based on a two-dimensional numerical model with volume of fluid method. Parametric ranges for generating alternating droplet formation (ADF) are identified. A physical background responsible for the ADF is suggested by analyzing the dynamical stability of flow system. Since the phase discrepancy between dispersed flows is mainly caused by non-symmetrical breaking of merging droplet, merging regime becomes the alternating regime at appropriate conditions. In addition, the effects of channel geometries on droplet formation are studied in terms of relative channel width. The predicted results show that the ADF region is shifted toward lower capillary numbers when channel width ratio is less than unity. The alternating droplet size increases with the increase of channel width ratio. When this ratio reaches unity, alternating droplets can be formed at very high water fraction (wf = 0.8). The droplet formation in MFDTD depends significantly on the viscosity ratio, and the droplet size in ADF decreases with the increase of the viscosity ratio. The understanding of underlying physics of the ADF phenomenon is useful for many applications, including nanoparticle synthesis with different concentrations, hydrogel bead generation, and cell transplantation in biomedical therapy.
Figures


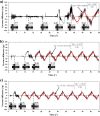

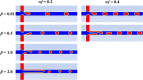
Similar articles
-
Review on Microbubbles and Microdroplets Flowing through Microfluidic Geometrical Elements.Micromachines (Basel). 2020 Feb 15;11(2):201. doi: 10.3390/mi11020201. Micromachines (Basel). 2020. PMID: 32075302 Free PMC article. Review.
-
Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions.Phys Rev E Stat Nonlin Soft Matter Phys. 2008 Sep;78(3 Pt 2):036317. doi: 10.1103/PhysRevE.78.036317. Epub 2008 Sep 18. Phys Rev E Stat Nonlin Soft Matter Phys. 2008. PMID: 18851153
-
Droplet formation in microfluidic T-junction generators operating in the transitional regime. II. Modeling.Phys Rev E Stat Nonlin Soft Matter Phys. 2012 Jan;85(1 Pt 2):016323. doi: 10.1103/PhysRevE.85.016323. Epub 2012 Jan 26. Phys Rev E Stat Nonlin Soft Matter Phys. 2012. PMID: 22400673
-
Modeling of Droplet Generation in a Microfluidic Flow-Focusing Junction for Droplet Size Control.Micromachines (Basel). 2021 May 21;12(6):590. doi: 10.3390/mi12060590. Micromachines (Basel). 2021. PMID: 34063839 Free PMC article.
-
Droplet breakup mechanisms in premix membrane emulsification and related microfluidic channels.Adv Colloid Interface Sci. 2021 Apr;290:102393. doi: 10.1016/j.cis.2021.102393. Epub 2021 Mar 2. Adv Colloid Interface Sci. 2021. PMID: 33770649 Review.
Cited by
-
Phase synchronization of fluid-fluid interfaces as hydrodynamically coupled oscillators.Nat Commun. 2020 Oct 15;11(1):5221. doi: 10.1038/s41467-020-18930-7. Nat Commun. 2020. PMID: 33060604 Free PMC article.
-
Design of an Adhesive Film-Based Microfluidic Device for Alginate Hydrogel-Based Cell Encapsulation.Ann Biomed Eng. 2020 Mar;48(3):1103-1111. doi: 10.1007/s10439-020-02453-9. Epub 2020 Jan 13. Ann Biomed Eng. 2020. PMID: 31933001 Free PMC article.
-
Review on Microbubbles and Microdroplets Flowing through Microfluidic Geometrical Elements.Micromachines (Basel). 2020 Feb 15;11(2):201. doi: 10.3390/mi11020201. Micromachines (Basel). 2020. PMID: 32075302 Free PMC article. Review.
References
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
