Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 May;200(1):321-9.
doi: 10.1534/genetics.114.173815. Epub 2015 Mar 10.

The evolutionarily stable distribution of fitness effects

Daniel P Rice  1 , Benjamin H Good  2 , Michael M Desai  3
Affiliations

The evolutionarily stable distribution of fitness effects

Daniel P Rice et al. Genetics. 2015 May.

Abstract

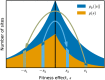
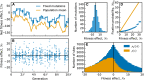
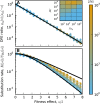
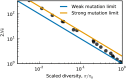
The distribution of fitness effects (DFE) of new mutations is a key parameter in determining the course of evolution. This fact has motivated extensive efforts to measure the DFE or to predict it from first principles. However, just as the DFE determines the course of evolution, the evolutionary process itself constrains the DFE. Here, we analyze a simple model of genome evolution in a constant environment in which natural selection drives the population toward a dynamic steady state where beneficial and deleterious substitutions balance. The distribution of fitness effects at this steady state is stable under further evolution and provides a natural null expectation for the DFE in a population that has evolved in a constant environment for a long time. We calculate how the shape of the evolutionarily stable DFE depends on the underlying population genetic parameters. We show that, in the absence of epistasis, the ratio of beneficial to deleterious mutations of a given fitness effect obeys a simple relationship independent of population genetic details. Finally, we analyze how the stable DFE changes in the presence of a simple form of diminishing-returns epistasis.

Keywords: distribution of fitness effects; evolutionary equilibrium; mutation–selection–drift balance.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The distribution of fitness effects of mutations, ρ(s), is the product of the distribution of absolute effect sizes, ρ0(|s|), and the allelic state of each site. A mutation changes the DFE by changing the allelic state at that site. For example, beneficial mutation with effect +s1 creates a potential back mutation with effect −s1. Likewise, a deleterious mutation with effect −s2 becomes the site of potential beneficial mutation with effect +s2.
Figure 2
Figure 2
An example of the steady-state dynamics, generated by a Wright–Fisher simulation of our model [N=104, NU=102, NR=0, ρ0(|s|)∼Exp[10/N], L=105]. (A) Time course of the mean fitness of the population and the cumulative effect of fixed mutations. (B) The fitness effect of each fixed mutation vs. its fixation time. (C) Histogram of the fitness effects of all fixed mutations. (D) The fixation probability of a beneficial mutation as a function of its fitness effect. Simulation results are shown as circles; the single-locus theory prediction in the absence of linked selection is shown as a solid line. (E) The distribution of absolute effects ρ0(|s|) (blue) and distribution of fitness effects ρ(s) (orange) measured at the end of the simulation.
Figure 3
Figure 3
The equilibrium DFE and steady-state substitution rate. (A) The equilibrium ratio of the beneficial mutation rate to the deleterious mutation rate for mutations with absolute effect |s|, averaged over 100 replicate simulations. Fitness effects are scaled by a parameter s˜, fitted to the average final DFE for each parameter set. The color of each line indicates the value of s˜ for each parameter set (inset). The solid black line shows exp(−s/s˜). (B) The substitution rate of mutations with absolute effect |s|, K(|s|), declines with the scaled fitness effect s/s˜. Upper and lower solid curves give the analytical results for the strong- and weak-mutation limits, respectively. All results here are for an asexual population with exponential ρ0(|s|). The results for other choices of ρ0(|s|) and for R>0 are equivalent (Figure S2).
Figure 4
Figure 4
Pairwise diversity predicts the equilibrium DFE ratio. For each parameter set, we fitted the scaling parameter s˜ to the equilibrium DFE and measured the average number of pairwise differences, π, normalized by the expected diversity in a neutrally evolving population of the same size, π0=2NU.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Berg, J., and M. Lässig, 2003 Stochastic evolution of transcription factor binding sites. Biophysics (Moscow) 48, Suppl. 1: 36–44.
    1. Berg J., Willmann S., Lässig M., 2004. Adaptive evolution of transcription factor binding sites. BMC Evol. Biol. 4: 42. - PMC - PubMed
    1. Burch C. L., Guyader S., Samarov D., Shen H., 2007. Experimental estimate of the abundance and effects of nearly neutral mutations in the RNA virus ϕ6. Genetics 176: 467–476. - PMC - PubMed
    1. Chou H.-H., Chiu H.-C., Delaney N. F., Segrè D., Marx C. J., 2011. Diminishing returns epistasis among beneficial mutations decelerates adaptation. Science 332: 1190–1192. - PMC - PubMed
    1. Comeron J. M., Kreitman M., 2002. Population, evolutionary, and genomic consequences of interference selection. Genetics 161: 389–410. - PMC - PubMed

Publication types

LinkOut - more resources