Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014;8 Suppl 5(Suppl 5):S1.
doi: 10.1186/1752-0509-8-S5-S1. Epub 2014 Dec 12.

Analytical study of robustness of a negative feedback oscillator by multiparameter sensitivity

Kazuhiro Maeda, Hiroyuki Kurata

Analytical study of robustness of a negative feedback oscillator by multiparameter sensitivity

Kazuhiro Maeda et al. BMC Syst Biol. 2014.

Abstract

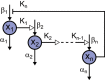
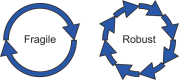
Background: One of the distinctive features of biological oscillators such as circadian clocks and cell cycles is robustness which is the ability to resume reliable operation in the face of different types of perturbations. In the previous study, we proposed multiparameter sensitivity (MPS) as an intelligible measure for robustness to fluctuations in kinetic parameters. Analytical solutions directly connect the mechanisms and kinetic parameters to dynamic properties such as period, amplitude and their associated MPSs. Although negative feedback loops are known as common structures to biological oscillators, the analytical solutions have not been presented for a general model of negative feedback oscillators.

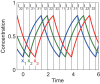
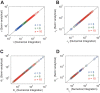
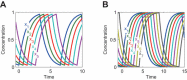
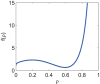
Results: We present the analytical expressions for the period, amplitude and their associated MPSs for a general model of negative feedback oscillators. The analytical solutions are validated by comparing them with numerical solutions. The analytical solutions explicitly show how the dynamic properties depend on the kinetic parameters. The ratio of a threshold to the amplitude has a strong impact on the period MPS. As the ratio approaches to one, the MPS increases, indicating that the period becomes more sensitive to changes in kinetic parameters. We present the first mathematical proof that the distributed time-delay mechanism contributes to making the oscillation period robust to parameter fluctuations. The MPS decreases with an increase in the feedback loop length (i.e., the number of molecular species constituting the feedback loop).

Conclusions: Since a general model of negative feedback oscillators was employed, the results shown in this paper are expected to be true for many of biological oscillators. This study strongly supports that the hypothesis that phosphorylations of clock proteins contribute to the robustness of circadian rhythms. The analytical solutions give synthetic biologists some clues to design gene oscillators with robust and desired period.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Schematic diagram of the negative feedback oscillator model. xi is the ith molecular species, αi is the decay rate constant, βi is the production rate constant, and Ki is the threshold for turning on/off the production of the target molecular species (i∈{1,2,…,n}). n is the number of molecular species. xi activates xi+1 (i∈{1,2,…,n-1}). xn represses x1. All molecular species are subject to degradation.
Figure 2
Figure 2
Example of dynamics of the negative feedback oscillator model. n=3, αi=1, βi=1 and Ki=0.5 (i∈{1,2,3}). Iij are the intervals used to derive the analytical solutions for the period and amplitude (see Text).
Figure 3
Figure 3
Comparison of the semi-analytical and numerical integration solutions . A: period, B: amplitude, C: period MPS, D: amplitude MPS. The values of αi and βi (i∈{1,2,…,n}) were randomized with a range of (0, 1), while the value of Ki (i∈{1,2,…,n}) was randomized with a range of (0, βi/αi).
Figure 4
Figure 4
Comparison of the full analytical and semi-analytical solutions. A: period, B: amplitude, C: period MPS, D: amplitude MPS. The values of αi and βi (i∈{1,2,…,n}) were randomized with a range of (0, 1), while the value of Ki (i∈{1,2,…,n}) was randomized with a range of (0, βi/αi).
Figure 5
Figure 5
Examples of dynamics of the negative feedback oscillator model. A: n=5, B: n=7. αi=1, βi=1 and Ki=0.5 (i∈{1,2,…,n}).
Figure 6
Figure 6
f(ρ) vs. ρ. f(ρ) is given by Eq (15) in Text.
Figure 7
Figure 7
Distributed time-delay mechanism. Oscillators with two (left) and eight (right) time delays. The right is more robust than the left because of the distributed time-delay mechanism (see Text).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Bell-Pedersen D, Cassone VM, Earnest DJ, Golden SS, Hardin PE, Thomas TL, Zoran MJ. Circadian rhythms from multiple oscillators: lessons from diverse organisms. Nat Rev Genet. 2005;6(7):544–556. doi: 10.1038/nrg1633. - DOI - PMC - PubMed
    1. Dunlap JC. Molecular bases for circadian clocks. Cell. 1999;96(2):271–290. doi: 10.1016/S0092-8674(00)80566-8. - DOI - PubMed
    1. Panda S, Hogenesch JB, Kay SA. Circadian rhythms from flies to human. Nature. 2002;417(6886):329–335. doi: 10.1038/417329a. - DOI - PubMed
    1. Tyson JJ, Novak B. Regulation of the eukaryotic cell cycle: molecular antagonism, hysteresis, and irreversible transitions. J Theor Biol. 2001;210(2):249–263. doi: 10.1006/jtbi.2001.2293. - DOI - PubMed
    1. Csete ME, Doyle JC. Reverse engineering of biological complexity. Science. 2002;295(5560):1664–1669. doi: 10.1126/science.1069981. - DOI - PubMed

Publication types

LinkOut - more resources