Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014:2014:820959.
doi: 10.1155/2014/820959. Epub 2014 Jul 3.

Modeling of scale-dependent bacterial growth by chemical kinetics approach

Haydee Martínez  1 , Joaquín Sánchez  1 , José-Manuel Cruz  2 , Guadalupe Ayala  3 , Marco Rivera  4 , Thomas Buhse  2
Affiliations

Modeling of scale-dependent bacterial growth by chemical kinetics approach

Haydee Martínez et al. ScientificWorldJournal. 2014.

Abstract

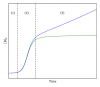
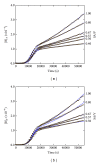
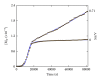
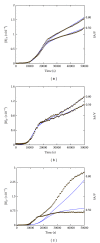
We applied the so-called chemical kinetics approach to complex bacterial growth patterns that were dependent on the liquid-surface-area-to-volume ratio (SA/V) of the bacterial cultures. The kinetic modeling was based on current experimental knowledge in terms of autocatalytic bacterial growth, its inhibition by the metabolite CO2, and the relief of inhibition through the physical escape of the inhibitor. The model quantitatively reproduces kinetic data of SA/V-dependent bacterial growth and can discriminate between differences in the growth dynamics of enteropathogenic E. coli, E. coli JM83, and Salmonella typhimurium on one hand and Vibrio cholerae on the other hand. Furthermore, the data fitting procedures allowed predictions about the velocities of the involved key processes and the potential behavior in an open-flow bacterial chemostat, revealing an oscillatory approach to the stationary states.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Sketch of typical SA/V-dependent EPEC growth curves ([B]T = total bacteria concentration): (1) lag phase and (2) exponential growth independent of the SA/V and (3) later stage growth depending on the SA/V. If the SA/V increases also the rate of the later stage growth increases. Note that under common laboratory culturing conditions the SA/V remains relatively small so that the later stage growth may look stationary (green curve) which, however, does not appear to be the case at higher SA/V ratios (blue curve).
Scheme 1
Scheme 1
Kinetic scheme composed of four irreversible processes to reproduce SA/V-dependent bacterial growth curves; B = aerobic bacteria, Ban = anaerobic bacteria, and N = nutrient. The parameter expression k 2/(k 4[CO2] + 1) in step (III) represents the autoinhibition by CO2 where k 4 is a control parameter to tune the inhibition strength. The reaction arrow in step (IV) symbolizes the physical escape of CO2 from the system.
Figure 2
Figure 2
Series of EPEC growth experiments with SA = 1.0 cm2 and V = 1.0 to 2.5 cm3 corresponding to SA/V = 0.4 to 1.0 cm−1 (open circles) best fitted by the CKA model (solid lines). (a) Fitting of each growth curve independently with obtained values for k 0 to k 4 according to Table 2. (b) Only fitting of k 3 at fixed k 0 = 6.46 M−1s−1, k 1 = 5.99 × 10−5 s−1, k 2 = 2.18 × 10−1 M−1s−1, and k 4 = 4.18 × 108 M−1. Obtained values for k 3 at different (SA/V): 1.29 × 10−5 (0.50), 6.18 × 10−5 (0.57), 1.07 × 10−4 (0.67), 2.97 × 10−4 (0.80), and 4.53 × 10−4 (1.00) s−1. Initial concentrations: [B] = 4.0 × 10−8, [O2] = 1.0 × 10−4, and [N] = 0.8 M, all others at zero.
Figure 3
Figure 3
EPEC growth curves at SA/V = 0.71 and 0 cm−1 with V = 1.4 cm3 in both cases (open circles) best fitted by the CKA model (solid lines). Obtained parameter values: k 0 = 7.87 M−1s−1, k 1 = 1.98 × 10−4 s−1, k 2 = 1.73 × 10−3 M−1s−1, k 3(0.71) = 6.55 × 10−3 s−1, k 3(0) = 0 s−1, and k 4 = 4.35 × 108 M−1.
Figure 4
Figure 4
Experimental growth curves of various bacteria (open circles) best fitted by the CKA model (solid lines). (a) E. coli JM83: SA/V = 0.5 and 0.8 cm−1, obtained parameter values are given in Table 3. (b) Salmonella typhimurium: SA/V = 0.5 and 0.8 cm−1, obtained parameter values are given in Table 3. (c) Vibrio cholerae: SA/V = 0.4 and 1.0 cm−1, shown curves illustrate that a satisfactory data fitting was rejected. All initial concentrations for the simulations are given in Figure 2.
Figure 5
Figure 5
Simulation of EPEC growth behavior in an open-flow bacterial chemostat predicting an oscillatory approach to the steady states of the total bacteria and oxygen concentrations. The same parameters as in Figure 3 (SA/V = 0.71), flow rate constants k 5 = k 6 = 2.0 × 10−6 s−1; [B]0 = 4.0×10−8, [O2]0 = 1.0 × 10−4, and [N]0 = 8.0 × 10−3 M, all others at zero.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Epstein IR, Pojman JA. An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns and Chaos. New York, NY, USA: Oxford University Press; 1998.
    1. Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics , Biology, Chemistry, and Engineering. Cambridge, Mass, USA: Perseus; 1994.
    1. Taub IA, Feeherry FE, Ross EW, Kustin K, Doona CJ. A quasi-chemical kinetics model for the growth and death of Staphylococcus aureus in intermediate moisture bread. Journal of Food Science. 2003;68(8):2530–2537.
    1. Doona CJ, Feeherry FE, Ross EW. A quasi-chemical model for the growth and death of microorganisms in foods by non-thermal and high-pressure processing. International Journal of Food Microbiology. 2005;100(1–3):21–32. - PubMed
    1. Ross EW, Taub IA, Doona CJ, Feeherry FE, Kustin K. The mathematical properties of the quasi-chemical model for microorganism growth-death kinetics in foods. International Journal of Food Microbiology. 2005;99(2):157–171. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources