Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2014 Jul 11:16:371-96.
doi: 10.1146/annurev-bioeng-121813-120704. Epub 2014 May 29.

Inertial focusing in microfluidics

Joseph M Martel  1 , Mehmet Toner
Affiliations
Review

Inertial focusing in microfluidics

Joseph M Martel et al. Annu Rev Biomed Eng. .

Abstract

When Segré and Silberberg in 1961 witnessed particles in a laminar pipe flow congregating at an annulus in the pipe, scientists were perplexed and spent decades learning why such behavior occurred, finally understanding that it was caused by previously unknown forces on particles in an inertial flow. The advent of microfluidics opened a new realm of possibilities for inertial focusing in the processing of biological fluids and cellular suspensions and created a field that is now rapidly expanding. Over the past five years, inertial focusing has enabled high-throughput, simple, and precise manipulation of bodily fluids for a myriad of applications in point-of-care and clinical diagnostics. This review describes the theoretical developments that have made the field of inertial focusing what it is today and presents the key applications that will make inertial focusing a mainstream technology in the future.

Keywords: applied physics; biofluid processing; high throughput; hydrodynamic lift; label-free cell separation; particle separation.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Early observations of inertial focusing in different microfluidic geometries. (a, top left) Schematic and image of inertial focusing in an asymmetrically curved microchannel. (bottom left) Longitudinal ordering in straight channels with the spacing measured to be multiples of 3.6 times the particle diameter at the same cross-sectional equilibrium positions. ACF is an autocorrelation function used to measure the spacing or lag between particles in an image (3). (right) Particle Reynolds number (ReP) effects in both straight and asymmetrically curved microchannels, visualized using confocal microscopy, with the reduction in the number of equilibrium positions from four to one in the curved channels. (b, top) Dean flow fractionation of two differently sized particles (purple, 1.9-μm diameter; green, 7.32-μm diameter). (Reproduced from 46 with permission from The Royal Society of Chemistry.) (bottom) Early spiral results showing focusing to half of the channel cross section in an extremely long (~2-m) spiral. (Reprinted with permission from 54. Copyright 2011, AIP Publishing LLC.) (c) Early use of expansion/contraction devices for focusing particles, showing the behavior at three positions along the device at increasing channel Reynolds number, ReC. (Panel reprinted with permission from 68. Copyright 2008, American Chemical Society.)
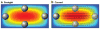
Figure 2
Figure 2
Velocity profile surface plot (red, high velocity; blue, zero velocity) (a) in a straight channel with the equilibrium positions highlighted and (b) in a slightly curved channel with vectors representing the Dean flow caused by the curvature of the channel. The opaque particles show the stable equilibrium positions, and the transparent particles are indicative of the stable positions in a straight channel made unstable under the correct conditions in a curved channel. Axial flow is into the page.
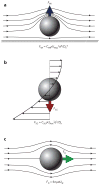
Figure 3
Figure 3
Schematics and equations describing the dominant forces in inertial focusing systems. (a) Wall interaction force: A particle moving near a wall will cause a pressure buildup on the wall side of the particle owing to the constricted flow on that side that imparts a force directed away from the wall. (b) Shear gradient lift force: A particle in a parabolic velocity field will experience a larger relative velocity on the side of the particle away from the inflection point (maximum of the parabola). This difference in velocity causes a pressure difference that imparts a force directed toward the higher-relative-velocity side of the particle. (c) Secondary-flow drag force: A particle in a uniform flow at low Reynolds number experiences a force relative to the difference between the particle velocity and the fluid velocity, also known as Stokes’ drag. Abbreviations: μ, fluid viscosity; ρ, fluid density; a, particle diameter; CSG, lift coefficient for the shear gradient lift force; CWI, lift coefficient for the wall interaction force; Dh, hydraulic diameter of the channel; FD, secondary-flow drag force; FSG, shear gradient lift force; FWI, wall interaction force; UMax, maximum velocity of the fluid; USF, secondary-flow velocity.
Figure 4
Figure 4
Results from highlighted empirical studies. (a) The negative (shear gradient lift and wall interaction forces) lift coefficient and positive (slower motion to the center of rectangular faces) lift coefficient. (Panel reproduced from 30 with permission from The Royal Society of Chemistry.) (b) Sample results from a study of focusing in curved channels, decoupling Reynolds and Dean numbers. Plots show the equilibrium behavior at each flow condition for particles of different diameter (red, 15 μm; green, 9.9 μm; blue, 4.4 μm). δ = (Dh/(2ReC))1/2 and is the Reynolds number–independent part of the Dean number (59). (c) Vortex formation in an expansion/ contraction device as well as the high-ReC behaviors of trapping large (10-μm) particles while allowing smaller (5-μm) particles to pass. (Panel reprinted with permission from 66. Copyright 2011, AIP Publishing LLC.) Abbreviations: a, particle diameter; FSG, shear gradient lift force; FWI, wall interaction force; FΩ, rotation-induced lift force; ReC, channel Reynolds number; UP, particle velocity.
Figure 5
Figure 5
Summarized effects of particle size, shape, and deformability on inertial focusing equilibrium behaviors. (a) Images of particles of different sizes equilibrating at different distances from a wall, with plots of these positions and associated rotation rates of spherical particles (38). (b, left) Photolithographic images of particles of different shapes focusing in a straight channel. (Reprinted with permission from Reference . Copyright 2011, AIP Publishing LLC.) (right) Oblong particles—made by melting and stretching spherical particles—focusing in a straight channel (75). (c) Droplets of different ratios of internal to surrounding fluid viscosity demonstrating the effect of deformability on inertial focusing in a straight channel. (Panel reproduced from 76 with permission from The Royal Society of Chemistry.) Abbreviations: FSG, shear gradient lift force; FWI, wall interaction force; ω, angular velocity; UP, particle velocity.
Figure 6
Figure 6
Highlighted applications of inertial focusing. (a) Sheathless alignment of cells in asymmetric curves for enhanced separation efficiency in magnetophoresis (96), showing cells (i) prior to focusing, (ii) after focusing, (iii) during magnetophoresis, and (iv) after complete separation. (b) Isolation of CTCs from blood cells by size in a spiral device. (Panel reprinted by permission from Macmillan Publishers Ltd: Scientific Reports from 103, copyright 2013.) (c) Bacteria filtration from blood using a straight inertial focusing channel (97). (Panel reprinted with permission; copyright 2010 Wiley Periodicals, Inc.) (d) Extraction of plasma from diluted blood in a spiral device. (Panel reprinted with permission from 106; copyright 2013, AIP Publishing LLC.) (e) Volume reduction of a sample of bioparticles using a spiral inertial focusing device. (Panel reprinted with permission from 57; copyright 2013, AIP Publishing LLC.) (f) Solution exchange in which a bead moves from one fluid to another in a straight channel of changing aspect ratio (110). (Panel reprinted with permission; copyright 2012, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.) Abbreviations: CTC, circulating tumor cell; De, Dean number.
Figure 7
Figure 7
Technologies enabled by inertial focusing behaviors. (a) Measurement of individual cell deformability characteristics for disease detection at a rate of thousands of cells per second (108). (b) Coupling of inertial ordering of cells and droplet encapsulation, which drastically improves the number of droplets created that hold a single cell and allows controlled encapsulation of particle pairs (114, 115). (c) Improved viability during electroporation by taking advantage of the spinning and vortexing of cells trapped in expansion/contraction devices. (Panel reproduced from 116 with permission from The Royal Society of Chemistry.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Pamme N. Continuous flow separations in microfluidic devices. Lab Chip. 2007;7:1644–59. - PubMed
    1. Gossett DR, Weaver WM, Mach AJ, Hur SC, Tse HTK, et al. Label-free cell separation and sorting in microfluidic systems. Anal Bioanal Chem. 2010;397:3249–67. - PMC - PubMed
    1. Di Carlo D, Irimia D, Tompkins R, Toner M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc Natl Acad Sci USA. 2007;104:18892–97. - PMC - PubMed
    1. Choi S, Song S, Choi C, Park JK. Hydrophoretic sorting of micrometer and submicrometer particles using anisotropic microfluidic obstacles. Anal Chem. 2008;81:50–55. - PubMed
    1. Loutherback K, Chou KS, Newman J, Puchalla J, Austin RH, Sturm JC. Improved performance of deterministic lateral displacement arrays with triangular posts. Microfluid Nanofluid. 2010;9:1143–49.