Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Nov 1;7(11):3608-3619.
doi: 10.1021/ct200389p.

On-the-fly Numerical Surface Integration for Finite-Difference Poisson-Boltzmann Methods

Qin Cai  1 , Xiang Ye  2 , Jun Wang  3 , Ray Luo  1
Affiliations

On-the-fly Numerical Surface Integration for Finite-Difference Poisson-Boltzmann Methods

Qin Cai et al. J Chem Theory Comput. .

Abstract

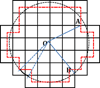
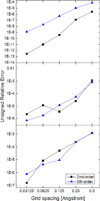
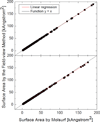
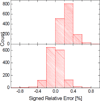
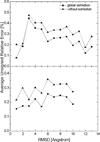
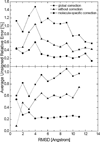
Most implicit solvation models require the definition of a molecular surface as the interface that separates the solute in atomic detail from the solvent approximated as a continuous medium. Commonly used surface definitions include the solvent accessible surface (SAS), the solvent excluded surface (SES), and the van der Waals surface. In this study, we present an efficient numerical algorithm to compute the SES and SAS areas to facilitate the applications of finite-difference Poisson-Boltzmann methods in biomolecular simulations. Different from previous numerical approaches, our algorithm is physics-inspired and intimately coupled to the finite-difference Poisson-Boltzmann methods to fully take advantage of its existing data structures. Our analysis shows that the algorithm can achieve very good agreement with the analytical method in the calculation of the SES and SAS areas. Specifically, in our comprehensive test of 1,555 molecules, the average unsigned relative error is 0.27% in the SES area calculations and 1.05% in the SAS area calculations at the grid spacing of 1/2Å. In addition, a systematic correction analysis can be used to improve the accuracy for the coarse-grid SES area calculations, with the average unsigned relative error in the SES areas reduced to 0.13%. These validation studies indicate that the proposed algorithm can be applied to biomolecules over a broad range of sizes and structures. Finally, the numerical algorithm can also be adapted to evaluate the surface integral of either a vector field or a scalar field defined on the molecular surface for additional solvation energetics and force calculations.

PubMed Disclaimer

Figures

Figure 1
Figure 1
A 2-D diagram of the finite-difference discretization of a sphere (black dash circle). Black solid lines are grid edges, whose intersection points denote grid points. O is the center of the sphere, A is the center of a square surface element or a grid edge, and B is an intersection point of the sphere and a grid edge. Red dash lines denote square surface elements at grid edge centers. The red dash lines can also be viewed as the finite-difference approximation of the spherical surface. The black solid arc represents a spherical surface element and the red solid line represents a square surface element that subtends the same solid angle, so they have the same flux passing through them.
Figure 2
Figure 2
Unsigned relative errors of numerical SES areas of simple geometries at successively fine grid spacings. Top: a single sphere, the radius of the sphere is 1.5Å; Middle: double spheres, the radii of the two spheres are both 1.5Å, the distance between the centers of the two spheres is 4Å; Bottom: triple spheres, the radii of the three spheres are all 1.5Å, the distance between one pair of spherical centers is 4Å, the distances between the other two pairs of spherical centers are both 3.606Å. The results are obtained from 100 area calculations with randomized grid orientations.
Figure 3
Figure 3
Convergence of the numerical SES areas versus grid spacings for 1BRV and 1FN2, respectively. Top: 1BRV (the field-view method converges to 1203.66Å2, the power order is 2.30; the MOLSURF result is 1203.69Å2); Bottom: 1FN2 (the field-view method converges to 1952.91Å2, the power order is 2.37; the MOLSURF result is 1952.90Å2). The uncertainty bars are estimated as the standard deviations from 100 FDPB calculations with randomized grid orientations. The uncertainty bars for the finer grid spacings are too small to be seen.
Figure 4
Figure 4
Convergence of the numerical SAS areas versus grid spacings for 1BRV and 1FN2, respectively. Top: 1BRV (the field-view method converges to 1661.15Å2, the power order is 0.70; the MOLSURF result is 1660.73Å2); Bottom: 1FN2 (the field-view method converges to 2777.78Å2, the power order is 2.36; the MOLSURF result is 2778.05Å2). Note that for 1BRV, only the data at fine grid spacings can be used in the extrapolation of the surface area.
Figure 5
Figure 5
Convergence rates of the numerical SES surface area and the numerical reaction field energy of 1BRV at successively fine grid spacings. Each result is obtained from 100 calculations with randomized grid orientations.
Figure 6
Figure 6
Correlation between the numerical surface areas of 1,555 molecules computed at the grid spacing of 1/2Å and the analytical surface areas by MOLSURF. Top: SES areas: AURE, 0.27%, slope, 0.99696, R-square, 1.00000; Bottom: SAS areas: AURE, 1.05%, slope, 0.97753, R-square, 0.99999.
Figure 7
Figure 7
Distributions of the signed relative errors of the numerical SES areas computed at the grid spacing of 1/2Å. Top: before correction, AURE, 0.27%; Bottom: after correction, AURE, 0.13%.
Figure 8
Figure 8
Correlation between the numerical surface areas and their signed relative errors. All the numerical surface areas were computed at the grid spacing of 1/2Å. Each data point represents the average signed relative error of the surface areas within a range of 0.5kÅ2. Top: SES areas; Bottom: SAS areas.
Figure 9
Figure 9
Average unsigned relative errors in the numerical SES areas after the global correction and without correction versus the backbone root-mean-square deviation (RMSD) for two tested peptides. Each data point represents the average unsigned relative error in the numerical surface areas for structures with the backbone RMSD within a range of 1Å with respect to the crystal structure. Top: hairpin; Bottom: helix. (grid spacing: 1/2Å)
Figure 10
Figure 10
Average unsigned relative errors in the numerical SAS areas after the global correction, without correction, and after molecule-specific corrections versus the backbone RMSD for two tested peptides. Each data point represents the average unsigned relative error in the numerical surface areas for structures with the backbone RMSD within a range of 1Å with respect to the crystal structure. Top: hairpin; Bottom: helix. (grid spacing: 1/2Å)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Lee B, Richards FM. J. Mol. Biol. 1971;55:379. - PubMed
    1. Richards FM. Annu. Rev. Biophys. Bio. 1977;6:151. - PubMed
    1. Im W, Beglov D, Roux B. Comput. Phys. Commun. 1998;111:59.
    1. Grant JA, Pickup BT, Nicholls A. J. Comput. Chem. 2001;22:608.
    1. Lu Q, Luo R. J. Chem. Phys. 2003;119:11035.

LinkOut - more resources